Recently, at Geektimes, I published an article where I gave some superficial statistics from a series of books "A Song of Ice and Fire." But I did not go into the most interesting part, the graph of social relations, because the topic deserves special attention. In this article, I will demonstrate how graph theory can help with the analysis of such data and give the implementation of the algorithms that I used.

Everyone who is interested, welcome to cat.

From a survey of the aforementioned article, I concluded that more than a third of the Geektimes audience are familiar with the fantasy novel of the novel, and more than half with the plot from the series. I hope that the audience of Geektimes and Habrahabr intersect and you may be interested not only in the algorithms used, but also in the results.

Data

Let's start, of course, with the main thing - data. We have a graph of social activity:



It depicts characters from the world of thrones at the vertices of the graph, where the size of the vertex depends on the words spoken by him, and character dialogs on the edges of the graph, where the thickness of the rib depends on the number of conversations held.

General information about the graph: The

graph is non-oriented.
Vertex (read characters): 1105
Ribs (read dialogs): 3505

This is all good, but who made a list of all the conversations, and even determined their affiliation, you ask me (in 5 books there are almost 2 million words ). Conditional random field method , I will answer. Yes, machine learning was used to collect data, and, as the “trainer” of the model states, the accuracy of determining the conversation’s affiliation is about 75%. I will add a questionnaire at the end of the article to find out whether to translate this article about how the conditional random field method was applied.

So, the input data format for all algorithms will be the same:

The first line contains V and E , the number of vertices and edges in the graph, respectively.

Next are V lines with the character ID and his name. After this, E lines of the form uvw are a description of the edges. Means that between u and v there is an edge with weight w , where u and v are IDcharacter. Let me remind you that weight means the number of dialogs between the respective characters. The weight of the vertices themselves will not be taken into account anywhere, because did not find a worthy application for him. Oh yes, the algorithm code will be presented in C ++.

We, of course, need to read the data. For this, I created the definitions.h and definitions.cpp files . Further, I will always connect definitions.h so that there is less code and the code is easier to read. Each subsequent algorithm is implemented as a separate function and is called in the main function .

Vertex degree

For starters, let's try to implement something very simple, which is even embarrassing to call an algorithm, but it will be interesting to the reader / viewer. Find the degree of each vertex. The degree of a vertex is the number of edges incident to (adjacent to) a vertex. This parameter in the context of the graph that we have will show us how many “friends” the character has.

This can be done in one pass and the complexity of this algorithm is O (V + E). If you apply and sort the result, as I did, then the complexity will be O (E + V * log (V)).


Top 10 multiply connected characters:

1. Tyrion Lannister: 168
   
2. John Snow: 128
   
3. Arya Stark: 104
   
4. Jamie Lannister: 102
   
5. Cersei Lannister: 86
   
6. Katileen Stark: 85
   
7. Theon Greyjoy: 76
   
8. Dineris Targaryen: 73
   
9. Brienne: 71
   
10. Sansa Stark: 69
    

The whole list

It is interesting that in the top there was no one who is familiar with many and is required to maintain contact with people, Varis (he is in 25th place). But, it would seem, the secondary character Brienne, on behalf of whom there is no chapter yet, is in 9th place.

Count traversal

So, now let's move on to simple algorithms, namely to search in depth ( Depth-first search ) and search in breadth ( Breadth-first search ). Both algorithms are very similar, they differ only in the way the graph is traversed. They are used when you need to go along the edges from a given vertex in the graph to another. In the case of a depth search, the graph runs from the top and alternately to the maximum depth along one of the outgoing edges. In the case of a breadth-first search, the graph goes around all its neighboring vertices first, then along the neighbors of neighboring vertices, and so on until there are no traversed vertices. Both algorithms have O (V + E) complexity.

Graph connectivity

Find the connected components of our graph. A connected component is a subgraph in which all vertices have a path to any other vertex of the component. To do this, run the search algorithm in depth at one of the vertices, and after completion, at the next vertex not marked with the algorithm. Thus, each search run will mean a new connectivity component.


It would be extremely strange if the graph were not connected and had more than one component in it, wouldn't it? But to my surprise, there were already 3 components in the graph! But looking at them, I saw that there was one big component, and 2 others, in which there was one character each (They were a smiling old man ( A smiley old man ), who talked with Arya near the God's eye ( God's eye ). And the cook ( A Cook ), who played with Tyrion on the ship). Nothing unusual, they have no names and it is surprising that the participants in the conversation generally decided correctly. Of course, I added the missing edges and as a result the whole graph turned out to be connected.

Handshake theory

Следующее что мы найдем с помощью алгоритма поиска уже в ширину — максимальное число рукопожатий в графе, другими словами диаметр графа, т.е наидлиннейший из кратчайших путей между всеми вершинами графа. Как оказалось, максимальное количество рукопожатий это 8. Неплохой результат для произведения о «средневековых веках», если учитывать Теорию 6ти рукопожатий. Для примера, одна из таких цепочек связи:

Матушка Кротиха (Mother Mole) — Репейница (Thistle) — Варамир (Varamyr) — Джон Сноу (Jon Snow) — Эддард Старк (Ned Stark) — Барристан Селми (Barristan Selmy) — Квентин Мартелл (Quentyn Martell) — Принц-Оборванец (The Tattered Prince) — Льюис Ланстер (Lewis Lanster)

Такой алгоритм работает за O(V*V+V*E). Так как нужно запустить алгоритм BFS из каждой вершины графа. Будь этот граф деревом, то потребовалось бы только 2 раза запустить BFS. Сначала из любой вершины графа, а затем из самой отдалённой от неё вершины. И наибольшая глубина последнего запуска и была бы диаметром графа.

А раз я нашёл самые длинные пути для всех вершин графа, то можно вычислить и среднее значение, а так же составить распределение максимальных путей. Среднее значение для длины максимальных путей оказалось 6,16 (в среднем вполне вписывается в теорию о 6ти рукопожатиях), а общее среднее расстояние 3,6, для сравнения у фейсбука этот параметр 4.57.

The distribution of the lengths of the maximum paths:



If you look at the distribution, we see that 77 characters are located in the "center" of the graph, in other words, they can communicate with any other character in no more than 4 others. Among them are all the main characters of the story, except Dineris Targaryen and Sansa Stark, and among those to whom less than five chapters are devoted in the books, Barristan Selmi, John Connington and Melisandra are on the list.

Whole result

Clicks in a graph

The Bron-Kerbosch algorithm allows you to find the maximum cliques in a graph, in other words, a subset of vertices, any two of which are connected by an edge. In the context of the graph in question, this will make it possible to find strongly related companies that have communicated among themselves in history. The complexity of the algorithm is linear with respect to the number of clicks in the graph, but in the worst case it is exponential O (3 ^{V / 3} ), the algorithm solves the NP complete problem all the same. The algorithm itself is a recursive function, which for each vertex finds the maximum click, i.e. one to which no other vertex can be added. So, the results:

Click size distribution:



As you can see, the maximum click size is 9 characters. For example, one of these is the Lannister company: Tyrion, Jamie, Cersei, Varis, Tywin, Kevan, Pitsel, Petir and Mace Tyrell. Interestingly, all clicks of size 8 and 9 are formed in or near Royal Harbor. A maximal clique with Dayneris size 5.

All results

Spanning tree

And now we will simplify our graph of connections a bit, leaving only the “backbone” in it, the so-called spanning tree , i.e. the most important communication edges and at the same time turning the graph into a tree with all the original vertices. The Kruskal algorithm will help us with this . The algorithm is greedy, for its implementation you just need to sort all the edges according to their weight and add each edge in turn, if it connects two components. If you use the correct data structure (usually a system of disjoint sets is used ), then the complexity of the algorithm is O (E (logE) + V + E) = O (E (logV)). Below is the result of the graph that underwent these manipulations. I also removed the edges with a weight of 1 for readability.

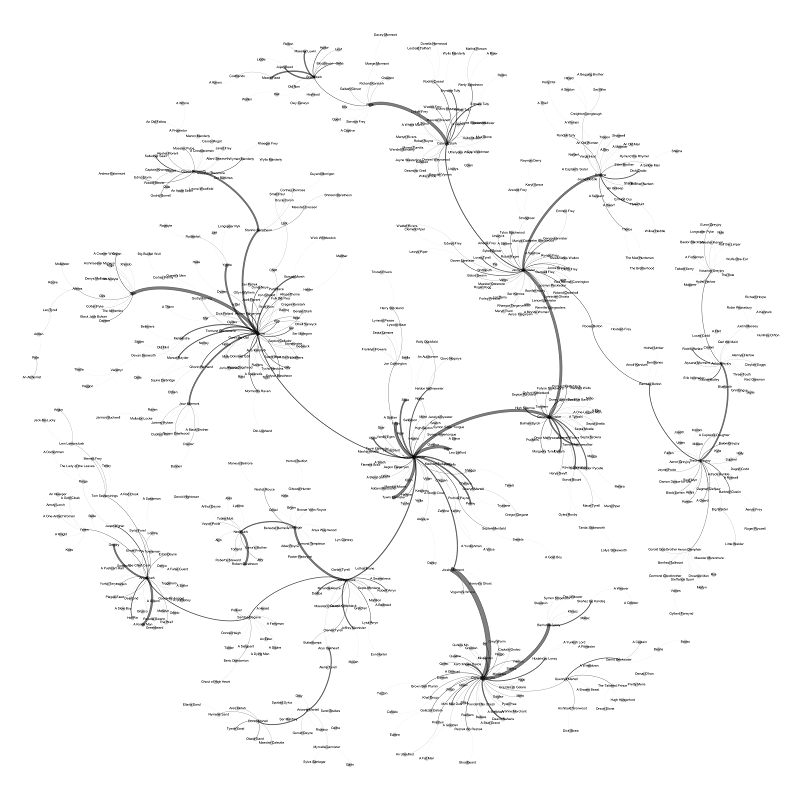
the picture is clickable.

So, from this graph you can see the main characters and their relationship with each other. As I expected, Tyrion Lannister is in the “center” of all connections, 4 large branches come from him: Cersei Lannister, John Snow, Sansa Stark and Jorah Mormont (Dineris branch). The latter, in turn, are the heroes of the next level in relations. Quite the expected result, is not it?

Whole result


But how many total spanning trees, including not only maximum ones, can be built? Incredibly much in this column, of course. But they can be calculated using the Kirchhoff theorem . The theorem says that if we construct a matrix where all elements of the adjacency matrix are replaced by opposite ones and the degrees of the corresponding vertices are on the main diagonal, then all algebraic additions of the resulting matrix will be equal and this value will be the number of spanning trees of the graph.

Bridges and hinges

Bridges in a graph are called edges, when removed, the number of connected components increases. The hinges have a similar definition, but unlike bridges, hinges are vertices, and when removed, the number of connected components increases. In this column, the presence of bridges will mean that in the world of thrones there are connections that are the only source of communication between individual groups of characters. Hinges, on the other hand, are heroes who are the only intermediaries for a group of other characters. Bridges and hinges are not very difficult to search. To do this, we need a familiar in depth search algorithm, but slightly modified. It is necessary to use the so-called time of entry to the top and the function of exit time ( fout) on the vertex, which will take the values ​​of the minimum entry time and the fout values ​​of the vertex into which the depth search has been passed, so if during the passage of the edge it turns out that the value of the fout function on the vertex is greater than the time of entering it, then this will be a bridge, and as well as a hinge, and if equal, then only a hinge. In other words, we check whether we return after traversing to the same edge / vertex and only to it when traversing part of the graph, if so, then this will be the desired bridge or hinge.

As expected, all hinges and bridges covered only insignificant characters. The number of vertices in the components that could be isolated by removing the hinges and bridges does not exceed 4x. This means that there is no hero who could not be sacrificed. All are interconnected through at least two other characters.

Whole result

Minimum cut

But it’s still interesting to know how many heroes need to be “killed” in order to completely exclude the contact of the two most popular (according to the above statistics) characters, say, Tirion Lannister and Arya Stark, or John Snow and Cersei Lannister. For this we will use the Dynits algorithm . First, let's figure out how the algorithm works.

By the Ford-Fulkerson Theoremit follows that the maximum flow in the path graph is equal to the throughput of its minimum cut. In other words, we can find the minimum cut between two vertices (sink and source) if we find the maximum flow between these vertices. The Dynits algorithm just allows you to find the maximum flow and, in fact, the flow itself. I will not analyze the algorithm in detail and will give you the opportunity to figure it out yourself. To understand the result, it is enough to know that the flow is a certain function that, for each edge lying on the path from the source to the drain, determines a positive value that does not exceed the throughput of this edge. To simplify, we can imagine a system of pipes with water, where the volume of water flowing from the source to the drain at time tand there is the magnitude of the flow.

The task I set is slightly different from the one that the algorithm solves. The fact is that the flow is determined on the edges, and if we find the minimum cut, then it will “cut” the graph along the edges, i.e. connections in the graph, but we really need to cut the graph not along edges, but vertices, i.e. characters. To solve this problem you need to subject the graph to small changes. Fork each vertex in the graph, say instead of the vertex v we get the vertices v ₁ and v ₂ , then if there was an edge between the two vertices v and u , then redirect v ₁ to u ₂ , and u ₁ tov ₂ , instead of the edge (u, v) we get the edges (v ₁ , u ₂ ) and (u ₁ , v ₂ ) . And between each forked vertices v ₁ and v ₂ we draw an edge (v ₂ , v ₁ ). In the received, already oriented, graph, all connections will be preserved, but where there were peaks before, edges will appear. If the weight of these edges is 1, and for all the others, say infinity (in practice, you can use the number of vertices in the graph), then the edge between the forked vertices will be the weakest link in the graph and, according to the “fuse” principle, will not allow a large stream to pass through itself, which will provide an opportunity to find out the number of vertices that need to be removed so that the graph becomes disconnected. Next, run the Dynits algorithm on the resulting graph.

The complexity of the algorithm is O (n ² m). Therefore, we will not search for the maximum flow value for all pairs of vertices, but only for the characters who have the greatest number of connections, otherwise for this graph the complexity will be O (n ⁵), where n = 1000 and everything will work for many hours. Below I will give the results for the top 100 characters on the links.

I was a little surprised by the results. It turned out that in the top 100, you can cut the graph by getting rid of at least 6 characters. All such connections in this case contain either John Connington or Euron Greyjoy as a drain / source. But these are not the main characters. Interestingly, in the top 10, basically the minimum flow is about 45. For example, between Tyrion and Arya the flow is 53, and between John Snow and Cersei 42. But there is also a character who can be separated by removing 16 other characters. This is Dineris Targaryen, not surprising, because she is the most distant heroine on the map of thrones.

It would also be interesting to know who the most “important” hero is in the streams. Those. through whom the maximum flow most often flows. There is something to be surprised at. Top 10 important characters in streams (in brackets is the corresponding number of entries in streams):

1. Tyrion Lannister (4109)
   
2. Jamie Lannister (3067)
   
3. Arya Stark (3021)
   
4. John Snow (2883)
   
5. Eddard Stark (2847)
   
6. Cersei Lannister (2745)
   
7. Theon Greyjoy (2658)
   
8. Brienne (2621)
   
9. Sandor Clegane (2579)
   
10. Sansa Stark (2573)
    

Firstly, Eddard Stark was an important character and, unfortunately (or fortunately) they are not spared. Secondly, Sandor Clegane, on whose behalf not a single chapter has been written, is still an important character. Thirdly, the top 10 characters are very tenacious, at least for now, but the most interesting is that the following 10 characters are:

11. Joffrey Lannister
12. Robb Stark
13. Renly Baratheon
14. Keithilyn Stark
15. Ruse Bolton
16. Joren
17. Sam
18. Melisandra
19. Bran Stark
20. Varis

where of the top 6 characters in the book are already killed 5. You will not envy the top ten. Who is next?

Also, thanks to the flows, it was possible to calculate the "extra" peaks, the replica authors of which could not be correctly recognized, therefore they were associated with many characters that they should not intersect with. They turned out to be Man (A Man) and Guardian (A Guard). As a result of which, I deleted these vertices and recounted all the statistics again.

Whole result


That's all. In conclusion, it can be noted that Tyrion Lannister is a very important character in the world of thrones. I hope the article has turned out to be interesting for you, and possibly useful. The source code of all the algorithms is also on GitHub, links below.

References:

GitHub project The
initial social graph Gephi
program , with which you can open the project Author of the headline photo - Adam Foster In the end, as promised, the questionnaire: is it worth translating the article on how the authors of dialogs in books were determined?