DIY audio codec is easy
- Tutorial
the current version of the article on the Makeloft website
I think that for many people, audio compression with losses resembles a magic black box, where in a surprisingly complex way, using mathematical alchemy, data is compressed due to the loss of redundant information, poorly visible or inaudible to the human ear, and, as a result, some decrease in quality records. However, immediately assessing the significance of such losses and understanding their essence is not very simple. But today we’ll try to find out what’s the matter there and due to which a similar process of compressing data by dozens of times is generally possible ...
It’s time to remove the curtain, open the door and take a personal look at the mysterious algorithm that excites the minds and hearts, welcome to the session with the exposure !
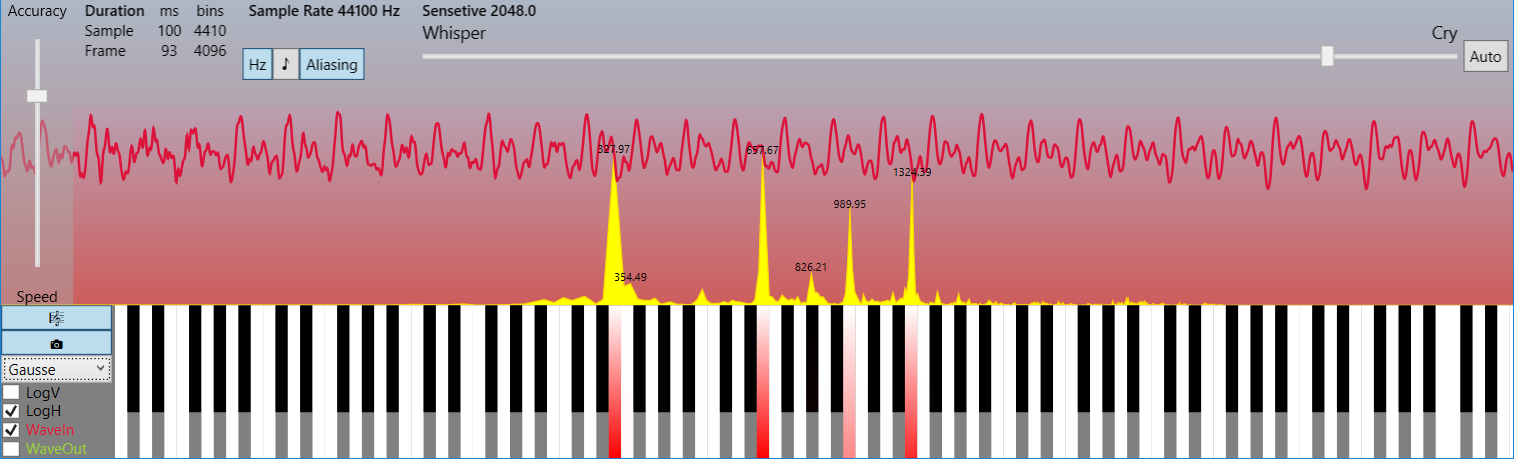
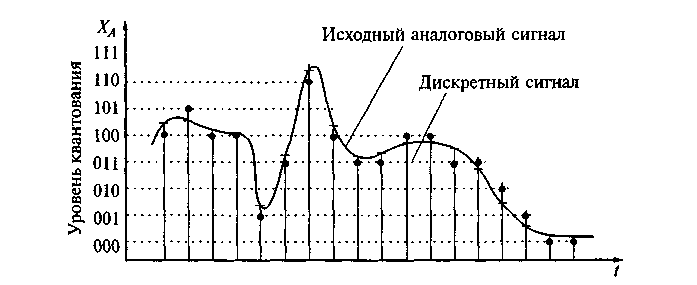
An uncompressed audio stream is an array of integers ( C # short ), for example, coming from a microphone buffer. It is a discrete set of values-amplitudes of an analog signal taken at regular intervals (that is, with a certain sampling rate and quantization by level).
* For simplicity, hereinafter we will consider the classic mono signal
If you immediately write this array to a file, then even a short time interval will turn out to be very voluminous. It is clear that, apparently, such a stream signal contains a lot of redundant data, so the question naturally arises, how to select the right one and remove the redundant one? The answer to it is simple and harsh - use the Fourier transform .
Yes, it’s the very thing that is regularly interpreted at technical universities and which we successfully manage to forget. However, this does not matter - we study the introductory presentation and read an article where the issue is considered in more than detail. We need only the algorithm itself, measuring just 32 lines of code in C # .
The conversion is applied to small portions of the signal - frames with the number of samples multiple of the power of two, which is usually 1024 , 2048 , 4096 . At a standard sampling frequency of 44100 Hz , which, according to the Kotelnikov-Nyquist-Shannon theorem, allows you to restore the original signal with a maximum frequency in the spectrum up to 22050 Hz without distortion , which corresponds to the maximum frequency threshold for audibility of the human ear, these passages are equivalent in duration to about 23 , 46 and 93 msrespectively. Then we get an array of complex numbers (the same length as the frame), which contains information about the phase and frequency spectra of this signal fragment. The resulting array consists of two mirror parts, copies, so only half of its elements have real information content.
At this stage, we can just remove information about quiet frequencies, preserving only loud ones , for example, in the form of a dictionary, and during playback, restore lost elements by replacing them with zero, then perform the inverse Fourier transform and get a signal suitable for playback. It is on this principle that the work of a huge number of audio codecs is based, since the described operation makes it possible to produce compression tens or even hundreds of times (!).Of course, the way of writing information to a file also makes its adjustments to the resulting size and it will not be superfluous to additionally use lossless archiving algorithms, but the most significant contribution is provided by the silencing of inaudible frequencies .
At first, I can’t believe that such significant compression ratios can be achieved in such a trivial way, but if you look at the spectral image on a linear frequency scale rather than the logarithmic one, it immediately becomes clear that in the real spectrum there is usually only a narrow set of harmonics that carry useful information, and everything else is a slight noise that lies beyond hearing. And, paradoxically, with small degrees of compression, the signal does not deteriorate for perception, but rather only clears itself of noise, that is, it is idealized!

* the pictures show a frame in 4096 samples (93 ms) and a frequency spectrum up to 22050 Hz (see LimitFrequency in source codes). This example demonstrates how few carrier harmonics in real signals.
In order not to be unfounded, I propose to test the demo application ( Rainbow Framework ) , where the compression algorithm is trivially simple, but quite functional. At the same time, you can evaluate the distortions that occur depending on the degree of compression, as well as learn how to visualize sound and much more ...
Yes, of course, there are puzzling algorithms that take into account the psycho-acoustic model of perception, the likelihood of certain frequencies appearing in the spectrum and so on and so forth, but all of them help to only partially improve performance while maintaining decent quality, while the lion's share of compression is achieved by such a simple in a way that in C # literally takes just a few lines.
So, the general compression scheme is as follows:
1. Splitting the signal into amplitude-time frames *
2. Direct Fourier transform - obtaining amplitude-frequency frames
3. Complete damping of quiet frequencies and additional optional processing
4. Writing data to a file
* often the frames partially overlap each other, which helps to avoid clicks when a certain harmonic signal starts or ends in one frame, but is still weak and will be muffled in it, although in another frame its sound is gaining full strength and is not muffled. Because of this, depending on the phase of the sinusoid, a sharp jump in amplitude is possible at the boundaries of non-overlapping frames, which is perceived as clicking.
The inverse process includes the following steps:
1. Reading a file
2. Recovering the amplitude-frequency frames
3. Inverse Fourier transform - obtaining amplitude-time frames
4. Generating a signal from the amplitude-time frames
That's all. Perhaps you expected something much more complicated?
References:
1.Introductory presentation
2. Article on Fourier transform
3. Demo application with source codes (Rainbow Framework)
( backup link )
I think that for many people, audio compression with losses resembles a magic black box, where in a surprisingly complex way, using mathematical alchemy, data is compressed due to the loss of redundant information, poorly visible or inaudible to the human ear, and, as a result, some decrease in quality records. However, immediately assessing the significance of such losses and understanding their essence is not very simple. But today we’ll try to find out what’s the matter there and due to which a similar process of compressing data by dozens of times is generally possible ...
It’s time to remove the curtain, open the door and take a personal look at the mysterious algorithm that excites the minds and hearts, welcome to the session with the exposure !

An uncompressed audio stream is an array of integers ( C # short ), for example, coming from a microphone buffer. It is a discrete set of values-amplitudes of an analog signal taken at regular intervals (that is, with a certain sampling rate and quantization by level).

* For simplicity, hereinafter we will consider the classic mono signal
If you immediately write this array to a file, then even a short time interval will turn out to be very voluminous. It is clear that, apparently, such a stream signal contains a lot of redundant data, so the question naturally arises, how to select the right one and remove the redundant one? The answer to it is simple and harsh - use the Fourier transform .
Yes, it’s the very thing that is regularly interpreted at technical universities and which we successfully manage to forget. However, this does not matter - we study the introductory presentation and read an article where the issue is considered in more than detail. We need only the algorithm itself, measuring just 32 lines of code in C # .
public static Complex[] DecimationInTime(this Complex[] frame, bool direct)
{
if (frame.Length == 1) return frame;
var frameHalfSize = frame.Length >> 1; // frame.Length/2
var frameFullSize = frame.Length;
var frameOdd = new Complex[frameHalfSize];
var frameEven = new Complex[frameHalfSize];
for (var i = 0; i < frameHalfSize; i++)
{
var j = i << 1; // i = 2*j;
frameOdd[i] = frame[j + 1];
frameEven[i] = frame[j];
}
var spectrumOdd = DecimationInTime(frameOdd, direct);
var spectrumEven = DecimationInTime(frameEven, direct);
var arg = direct ? -DoublePi / frameFullSize : DoublePi / frameFullSize;
var omegaPowBase = new Complex(Math.Cos(arg), Math.Sin(arg));
var omega = Complex.One;
var spectrum = new Complex[frameFullSize];
for (var j = 0; j < frameHalfSize; j++)
{
spectrum[j] = spectrumEven[j] + omega * spectrumOdd[j];
spectrum[j + frameHalfSize] = spectrumEven[j] - omega * spectrumOdd[j];
omega *= omegaPowBase;
}
return spectrum;
}
The conversion is applied to small portions of the signal - frames with the number of samples multiple of the power of two, which is usually 1024 , 2048 , 4096 . At a standard sampling frequency of 44100 Hz , which, according to the Kotelnikov-Nyquist-Shannon theorem, allows you to restore the original signal with a maximum frequency in the spectrum up to 22050 Hz without distortion , which corresponds to the maximum frequency threshold for audibility of the human ear, these passages are equivalent in duration to about 23 , 46 and 93 msrespectively. Then we get an array of complex numbers (the same length as the frame), which contains information about the phase and frequency spectra of this signal fragment. The resulting array consists of two mirror parts, copies, so only half of its elements have real information content.
At this stage, we can just remove information about quiet frequencies, preserving only loud ones , for example, in the form of a dictionary, and during playback, restore lost elements by replacing them with zero, then perform the inverse Fourier transform and get a signal suitable for playback. It is on this principle that the work of a huge number of audio codecs is based, since the described operation makes it possible to produce compression tens or even hundreds of times (!).Of course, the way of writing information to a file also makes its adjustments to the resulting size and it will not be superfluous to additionally use lossless archiving algorithms, but the most significant contribution is provided by the silencing of inaudible frequencies .
At first, I can’t believe that such significant compression ratios can be achieved in such a trivial way, but if you look at the spectral image on a linear frequency scale rather than the logarithmic one, it immediately becomes clear that in the real spectrum there is usually only a narrow set of harmonics that carry useful information, and everything else is a slight noise that lies beyond hearing. And, paradoxically, with small degrees of compression, the signal does not deteriorate for perception, but rather only clears itself of noise, that is, it is idealized!

* the pictures show a frame in 4096 samples (93 ms) and a frequency spectrum up to 22050 Hz (see LimitFrequency in source codes). This example demonstrates how few carrier harmonics in real signals.
In order not to be unfounded, I propose to test the demo application ( Rainbow Framework ) , where the compression algorithm is trivially simple, but quite functional. At the same time, you can evaluate the distortions that occur depending on the degree of compression, as well as learn how to visualize sound and much more ...
var fftComplexFrequencyFrame = inputComplexTimeFrame.DecimationInTime(true);
var y = 0;
var original = fftComplexFrequencyFrame.ToDictionary(c => y++, c => c);
var compressed = original.OrderByDescending(p => p.Value.Magnitude).Take(CompressedFrameSize).ToList();
Yes, of course, there are puzzling algorithms that take into account the psycho-acoustic model of perception, the likelihood of certain frequencies appearing in the spectrum and so on and so forth, but all of them help to only partially improve performance while maintaining decent quality, while the lion's share of compression is achieved by such a simple in a way that in C # literally takes just a few lines.
So, the general compression scheme is as follows:
1. Splitting the signal into amplitude-time frames *
2. Direct Fourier transform - obtaining amplitude-frequency frames
3. Complete damping of quiet frequencies and additional optional processing
4. Writing data to a file
* often the frames partially overlap each other, which helps to avoid clicks when a certain harmonic signal starts or ends in one frame, but is still weak and will be muffled in it, although in another frame its sound is gaining full strength and is not muffled. Because of this, depending on the phase of the sinusoid, a sharp jump in amplitude is possible at the boundaries of non-overlapping frames, which is perceived as clicking.
The inverse process includes the following steps:
1. Reading a file
2. Recovering the amplitude-frequency frames
3. Inverse Fourier transform - obtaining amplitude-time frames
4. Generating a signal from the amplitude-time frames
That's all. Perhaps you expected something much more complicated?
References:
1.Introductory presentation
2. Article on Fourier transform
3. Demo application with source codes (Rainbow Framework)
( backup link )
