We analyze strange correlations

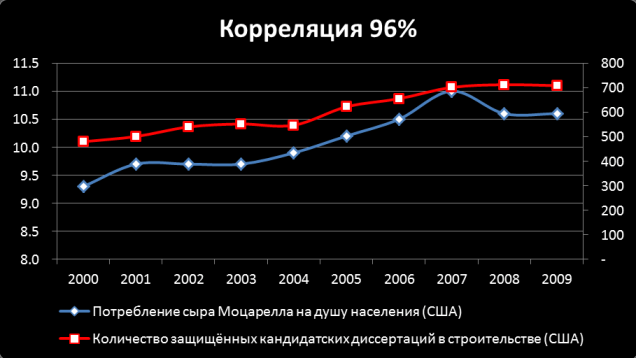
Recently I noticed a link to an article in a Facebook feed with a bunch of examples of “strange correlations” like in the picture. The source is here , and there are about 20 such examples. I decided to practice in statistics and check how surprising these correlations really are.

Interested please under cat.

We remove trends

If two indicators grow all the time, then they will have a positive correlation, and this is not surprising. Correlation needs to be measured in stationary variables. To remove trends, I built a linear regression from time to time for each indicator, subtracted from the actual data and checked the correlation of the residuals.

In some cases, the correlation is greatly reduced:



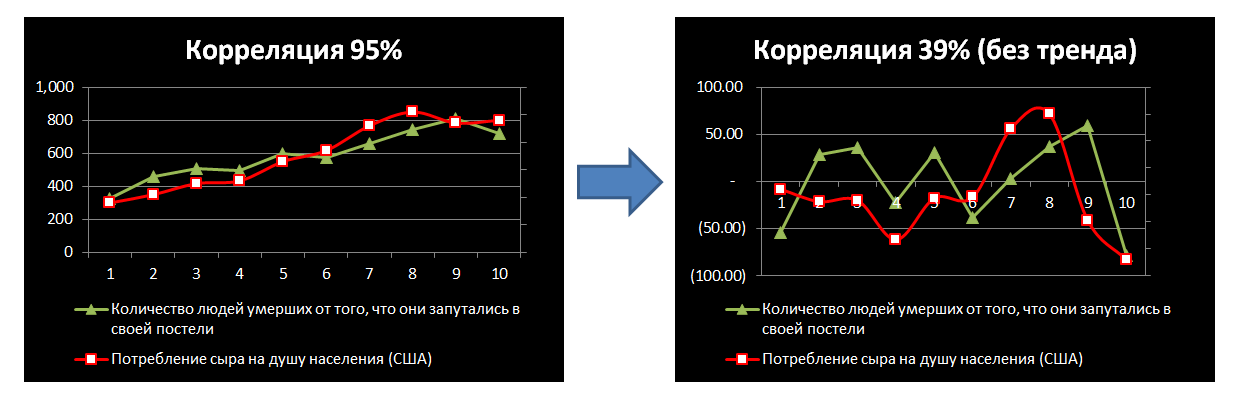
In others, nothing has changed:



So there must be something else!

By the way, I noticed that there are significantly more positive correlations than negative ones. I think the fact is that in the database of indicators used by the author, there are a lot of growing indicators. People generally like to measure something growing. As a result, a bunch of indicators for which the “residuals from the trend” have a strong negative correlation were not found, since the coincident positive trend shifted the correlation closer to zero.

What is the probability of getting such a correlation by chance?

Here we take up the formulas! It turned out that on average in these variables there are 11 points and after correction for trends, the average correlation is around 70%. Knowing the correlation and the number of points, you can get a variable that is distributed as a t-student with the number of degrees of freedom n-2:



We get t = 2.98 and the probability of obtaining such a correlation for independent variables is about 0.77%. The resulting figure is quite impressive, but the question is not closed!

And what about the twin paradox?

The probability of 0.77% seems too low to believe in an accidental coincidence, but intuition is wrong here. This situation is similar to the well-known birthday paradox. The

probability that two people were born on the same day is 1/365. But among only 23 people with a 50% probability, there will be a couple born on the same day. This happens because we don’t care what kind of two people it will be, and among 23 people you can make many pairs.

The same thing happens with the correlation of various indicators, if it does not matter which of them will correlate. Two random variables will strongly correlate in one attempt out of 65. I multiply the probability by 2, since a correlation below -70% also interests us.



But if you take only 9 random variables (11 points each), then with a probability of 50% there will be a correlation of more than 70% or less - 70%



In practice, I probably had to look at a lot more variables. A lot of indicators can actually or should correlate and filter out the “amazing” ones that were difficult. But after a statistical analysis it is clear that there is nothing surprising in the indicators found. Again, intuition fails a person to assess probability.