Comparing Audio Recognition Algorithms for Second Screen

Introduction

Today, there are many sound recognition methods. In its most general form, most methods consist of an algorithm for constructing a signature (fingerprints) of a signal (the most compact and at the same time most accurately describing the track of a set of attributes), an algorithm for its search in the database, and an algorithm for cutting off false positives. We were faced with the task of choosing a technology for building second screen applications.

Moreover, a comparison of recognition algorithms based on known accuracy characteristics is rather arbitrary, since these characteristics were obtained on different test data and for different errors of the first kind (false positives). Also, based on the context of the task, we were interested in the effectiveness of the algorithm in relation to the recognition of the audio signal of the air, with distortions due to the microphone parameters of modern mobile devices.

Since no comparative data satisfying our requirements were found in open sources, it was decided to conduct our own study of sound recognition algorithms, taking into account the specifics of the audio stream and distortions. As potential candidates, we chose the algorithms J. Haitsma and A. Wang. Both are widely known and based on the analysis of time-frequency characteristics obtained using the window Fourier transform.

Description of Signature Building Methods

The audio signal signature construction scheme proposed by Jaap Haitsma and Ton Kalker in [1] is shown in Figure 1. Table 1 shows the images obtained at each stage of the algorithm.

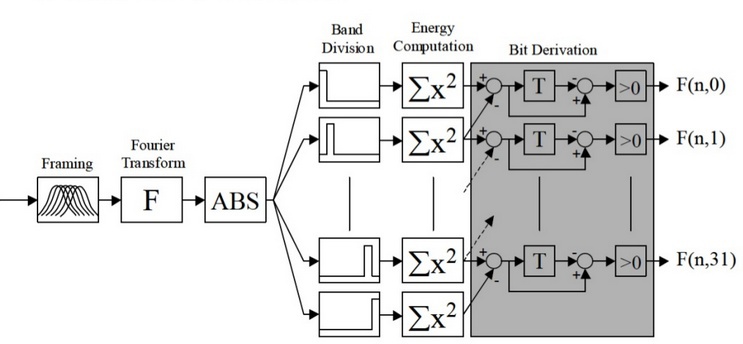Figure 1 - Jaap Haitsma and Ton Kalker signature building diagram

The signal spectrogram is constructed using the Hann window with an overlap of 31/32. For example, for a window size of 0.37 s, the sampling step of the spectrogram along the time axis is 11.6 ms. In the next step, the algorithm divides the frequency axis into 33 subbands on the mel scale, and for each moment in time, the total energy in the subband is calculated. The resulting temporary energy distribution is encoded in accordance with the expression:


where 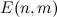is the energy of the ith frame in the subband .

Table 1 - The main stages of building a signature Jaap Haitsma and Ton Kalker

Signal snippet
Original	Distorted
Spectrogram construction
Calculation of energy distribution over subbands
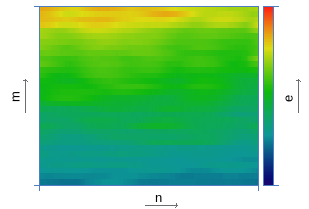Energy Distribution Coding

Thus, each 11.6 ms signal interval is described by a 32-bit word. As shown by experimental studies [1], 256 words are sufficient for reliable and stable to many types of recognition distortions, which corresponds to a 3 second query.

The recognition approach proposed by Avery Li-Chun Wang [2] is based on the peaks of the amplitude of the spectrogram and their relationships in pairs, called constellations.

The main difficulty in implementing this approach is the search algorithm for distortion resistant peaks. In [3, 4], examples of relevant techniques are presented. Among the many local maxima of the spectrogram, peaks with maximum energy are selected. Moreover, in order for the track description to be resistant to noise, it is necessary to ensure their diversity in frequency and time. For this, various blurring and threshold clipping techniques are used [3, 4]. The spectrogram of an audio track, as a rule, is divided into frames along the time axis, each of which is characterized by a certain number of peaks. By limiting their density in this way, it is possible to leave the peaks with the maximum probability of survival, and at the same time describe in detail the change in the spectrum with time. As an example, table 2 presents the images obtained at the main stages of the algorithm.

Table 2 - The main stages of building the signature proposed by A. Wang

Signal snippet
Original	Distorted
Spectrogram construction
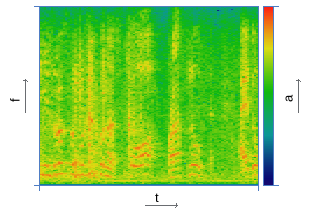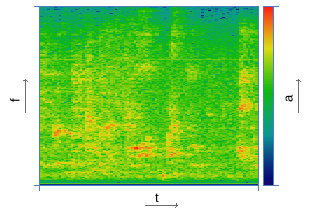Peak Search
Pairing peaks

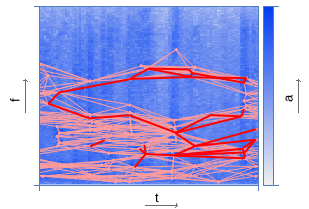To speed up the search process, peaks are combined in pairs - each peak is associated with a number of other peaks located to the right along the time axis within a specific target zone. The acceleration coefficient is approximately estimated by the equation:


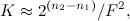
where and is the number of bits required to encode the peak and their pairs, respectively;
- the number of peaks associated with the reference (branching coefficient).

Moreover, an increase in the uniqueness of a hash is accompanied by a decrease in the probability of its survival, which is approximately estimated as:


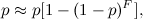
where 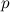is the probability of survival of the peak of the spectrogram.
Therefore, it is necessary to find the values ​​of the peak density and the branching coefficient 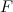, which provides a compromise between the search speed and the probability of signal recognition.

A signal signature consists of two components: a hash of a pair and a code for its displacement along the time axis. The minimum number of bits required to encode a pair is determined by the equation:


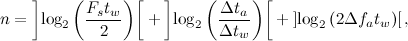
where 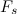is the sampling frequency of the signal; 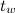, 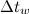- size and step of the window used in the construction of the spectrogram; , - respectively, the maximum allowable distance along the time axis and the frequency axis between the peaks of the pair; - taking the nearest largest integer.

Experimental Results

Based on the field of use, the comparison of the recognition approaches considered above was carried out on the basis of audio tracks of the television broadcast with a total duration of 2000 min. As test signals, we used recordings of original tracks played on a TV and recorded on iPhone 4, Nexus 7, Samsung GT3100 mobile devices at different distances from the signal source in the presence of extraneous noise characteristic of the environment. The test mono signals had a sampling frequency of 8 kHz with an amplitude encoding of 16 bits. Of these, 2,000 test queries were generated with a duration of 4 s.

When using the J. Haitsma signature, the search was carried out using the brute force method - a direct comparison of the query with each fragment in the database based on the Hamming metric. A request was considered to be found if, by bitwise comparison, its signature and the signature of the found fragment coincided by more than 65%.

Signatures were built on Wang principles with a Hann window size of 64 ms, with a shift of 32 ms. An own version of the search for peaks of the spectrogram was implemented, which was more suitable for recognizing the audio signal of the air compared to the prototype [3]. A fragment with a duration of 4 s was characterized on average by 200 peaks and was described by 1000 pairs. To make a decision, we used the formalization of the concept of uniqueness of a peak on the score graph for each answer option available in the database. The request was considered recognized if the score was unique.

Table 3 shows the accuracy results of the recognition algorithms obtained. The audio fragment was considered correctly recognized if the original track and the request offset in it were correctly identified.

Table 3 - Comparison of the accuracy of recognition algorithms

Algorithm	Mobile device
	iPhone 4		Nexus 7		Samsung GT3100
	fp ,%	fn ,%	fp ,%	fn ,%	fp ,%	fn ,%
J. Haitsma, T. Kalker	0.6	8	0.6	10	0.5	9
Based on the principles of A. Wang	0.6	20	0.6	25	0.6	24
Note: fp - errors of the first kind (false positives); fn - errors of the second kind (false negatives).

Conclusion

The J. Haitsma algorithm uses an integrated approach to describe the distribution of energy over frequency subbands, a differential approach to encode its change in time, and a comparison of signatures based on Hamming distance. All this makes this method potentially resistant to distortion. At the same time, the proportion of coincident pairs of peaks of the spectrogram ranges from 1% to 3%, which does not have the best effect on noise immunity and leads to a loss in recognition probability.

However, to use the full potential of J. Haitsma signatures, a query search in the database must be performed using the brute force method. Our implementation of the algorithm for the GPU on the Radeon R9 290X graphics card provides a parallel search of 2048 queries in 0.6 s. A server written using the libevent library can withstand a load of 1900 rps, with an average response time of 0.8 s. At the same time, industrial video cards are expensive, and ordinary ones have to be installed in standard ATX cases, which have a size of at least 3 units. In one such case, we managed to place two cards. At the same time, our implementation of the recognition server based on the principles of A. Wang, on a Xeon machine, the CPU E5-2660 v2 @ 2.20GHz / 32Gb can withstand a load of 2500 rps with an average response time of 8 ms.

I would like to note that we do not exclude the possibility of obtaining more optimal implementations of the algorithms, and the results should be treated as evaluative, not claiming absoluteness.

List of references

1. Jaap Haitsma, Ton Kalker “A Highly Robust Audio Fingerprinting Syste”
2. Avery Li-Chun Wang "An Industrial-Strength Audio Search Algorithm"
3. D. Ellis “Robust Landmark-Based Audio Fingerprinting”
4. E. Crofto “How Yandex recognizes music from a microphone”