Mass stacking of ML models in production: is it real or not?
We are often asked why we are not organizing data scientist contests. The fact is that we know from experience: the solutions in them are not at all applicable to prod. Yes, and to hire those who will be in the leading places, does not always make sense.
Such competitions are often won by the so-called Chinese stacking, when in a combinatorial way they take all possible algorithms and values of the hyperparameters, and the resulting models in several levels use the signal from each other. Ordinary satellites of these solutions - complexity, instability, difficulty in debugging and support, a very large resource intensity in training and forecasting, the need for careful supervision of a person in each cycle of repeated training of models. The meaning of doing this is only at competitions - for the sake of ten thousandths in local metrics and positions in the standings.
About a year ago, we decided to try to apply stacking in production. It is known that linear models allow extracting a useful signal from texts presented in the form of bag of words and vectorized using tf-idf, despite the large dimension of such vectors. Our system has already produced such a vectorization, so it was not very difficult for us to combine vectors for resumes, vacancies and, based on them, to teach logistic regression so that it predicted the probability of a candidate clicking with a given resume for a given vacancy.
Then this prediction is used by the main models as an additional attribute, since the model considers the meta-attribute. The beauty is that even with the ROC AUC 0.7, the signal from such meta-attribute patterns is useful. The implementation gave about 2 thousand responses per day. And most importantly - we realized that we can move on.
The linear model does not take into account non-linear interactions between features. For example, it cannot take into account that if there is an “C” in the resume, and a “system programmer” in the vacancy, the probability of response becomes very large. In addition, the vacancy and resume, in addition to the text, have many numerical and categorical fields, and in the resume, the text is divided into many separate blocks. Therefore, we decided to add a quadratic trait expansion for linear models and iterate over all possible combinations of tf-idf-vectors from fields and blocks.
We tried meta-signs that predict the likelihood of response under various conditions:
Then, with the help of feature selection, those dozens of meta-attributes that selected the maximum effect were selected, A / B tests were performed and released in production.
As a result, we received more than 23 thousand new responses per day. Some of the signs entered the top signs of strength.
For example, in a recommender system, top features are
in a logistic regression model that filters suitable summaries:
in the model on XGBoost, filtering suitable summaries:
in the ranking model on XGBoost:
A good result shows that a certain number of responses and invitations per day can be extracted from this direction with the same marketing costs.
For example, it is known that with a large number of signs in a logistic regression, the probability of retraining increases.
Suppose we use tf-idf vectorizer for texts of CVs and vacancies with a dictionary of 10 thousand words and phrases. Then in the case of a quadratic expansion in our logistic regression will be 2 * 10 000 + 10 000² weights. It is clear that with such a sparseness even individual cases can significantly affect each individual weight “in the summary there was a rare word such and such — in a vacancy such and such — the user clicked”.
Therefore, now we are trying to make meta-signs on logistic regression, in which the coefficients of quadratic expansion are compressed using factorization machines. Our 10,000² weights are represented as a matrix of latent vectors of dimension, for example, 10,000x150 (where we chose the dimension of the latent vector 150 ourselves). In this case, individual cases of compression cease to play a large role, and the model begins to better take into account more general patterns, and not to memorize specific cases.
We also use meta-signs on the DSSM neural networks, which we have already written about , and on ALS, which we also wrote about , but in a simplified way. In total, the introduction of meta-signs to date has given us (and our customers) more than 44 thousand additional responses (leads) to vacancies per day.
As a result, the simplified model stacking scheme in vacancy recomendations has now become:
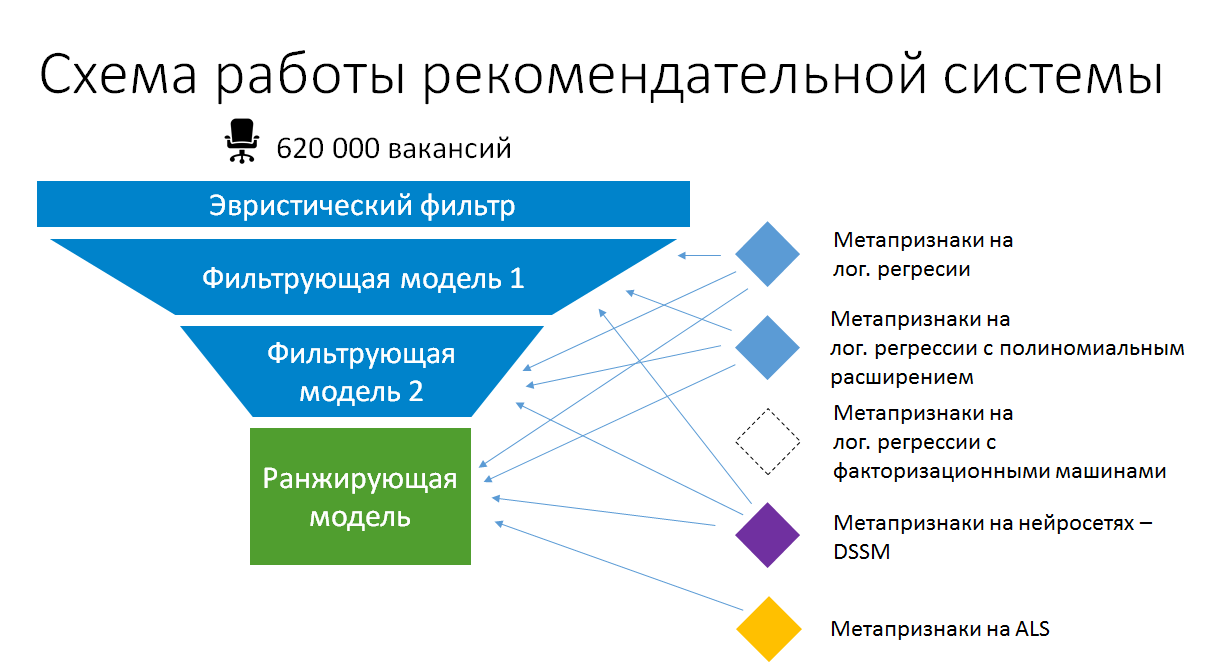
Thus, stacking in production makes sense. But this is not the automatic, combinatorial stacking. We make sure that the models on the basis of which meta-attributes are created remain simple and use the existing data and the calculated static features to the maximum extent. Only in this way can they remain in production without gradually becoming an unsupported black box, and remain in a state where they can be retrained and improved.

Such competitions are often won by the so-called Chinese stacking, when in a combinatorial way they take all possible algorithms and values of the hyperparameters, and the resulting models in several levels use the signal from each other. Ordinary satellites of these solutions - complexity, instability, difficulty in debugging and support, a very large resource intensity in training and forecasting, the need for careful supervision of a person in each cycle of repeated training of models. The meaning of doing this is only at competitions - for the sake of ten thousandths in local metrics and positions in the standings.
But we tried
About a year ago, we decided to try to apply stacking in production. It is known that linear models allow extracting a useful signal from texts presented in the form of bag of words and vectorized using tf-idf, despite the large dimension of such vectors. Our system has already produced such a vectorization, so it was not very difficult for us to combine vectors for resumes, vacancies and, based on them, to teach logistic regression so that it predicted the probability of a candidate clicking with a given resume for a given vacancy.
Then this prediction is used by the main models as an additional attribute, since the model considers the meta-attribute. The beauty is that even with the ROC AUC 0.7, the signal from such meta-attribute patterns is useful. The implementation gave about 2 thousand responses per day. And most importantly - we realized that we can move on.
The linear model does not take into account non-linear interactions between features. For example, it cannot take into account that if there is an “C” in the resume, and a “system programmer” in the vacancy, the probability of response becomes very large. In addition, the vacancy and resume, in addition to the text, have many numerical and categorical fields, and in the resume, the text is divided into many separate blocks. Therefore, we decided to add a quadratic trait expansion for linear models and iterate over all possible combinations of tf-idf-vectors from fields and blocks.
We tried meta-signs that predict the likelihood of response under various conditions:
- in the job description there is a given set of terms, categories;
- a specific set of terms has been encountered in the vacancy text box and the resume text box;
- a certain set of terms was encountered in the vacancy text field that was not met in the resume text field;
- certain terms have been encountered in a vacancy, the specified category value has been met in the summary;
- in the vacancy and resume met given a pair of category values.
Then, with the help of feature selection, those dozens of meta-attributes that selected the maximum effect were selected, A / B tests were performed and released in production.
As a result, we received more than 23 thousand new responses per day. Some of the signs entered the top signs of strength.
For example, in a recommender system, top features are
in a logistic regression model that filters suitable summaries:
- geographical region of the summary;
- resume profile;
- the difference between the job description and the latest work experience;
- the difference of geographic regions in the vacancy and resume;
- the difference between the title of the vacancy and the title of the resume;
- the difference between specializations in vacancies and resumes;
- the likelihood that an applicant with a certain salary in a resume will click on a vacancy with a certain salary (a meta-sign on the logistic regression);
- the likelihood that a person with a specific resume name will click on vacancies with a certain work experience (a meta-attribute on logistic regression);
in the model on XGBoost, filtering suitable summaries:
- how similar are the vacancy and resume;
- the difference between the name of the vacancy and the name of the resume and all positions in the experience in the resume, taking into account textual interactions;
- the difference between the name of the vacancy and the name in the resume, taking into account textual interactions;
- the difference between the name of the vacancy and the name of the resume and all positions in the experience of the resume, excluding textual interactions;
- the likelihood that a candidate with the specified work experience will go to a vacancy with that title (a meta-sign on logistic regression);
- the difference between the job description and previous job experience in the resume;
- how much vacancy and resume differ in the text;
- the difference between the job description and previous job experience in the resume;
- the probability that a person of a certain sex will respond to a vacancy with a certain name (a meta-sign on a logistic regression).
in the ranking model on XGBoost:
- the probability of response in terms that are present in the title of the vacancy and are absent in the name and position of the summary (meta-sign on the logistic regression);
- coincidence of region from vacancy and resume
- the probability of response in terms that are present in the vacancy and are absent in the summary (a meta-attribute on the logistic regression);
- the predicted attractiveness of the vacancy for the user (meta-sign on ALS);
- probability of response in terms that are present in a job and resume (a meta-sign on logistic regression);
- the distance between the title of the vacancy and the title + position from the summary, where the terms are weighted by user actions (interaction);
- the distance between the specializations of the vacancy and resume;
- the distance between the title of the vacancy and the name from the summary, where the terms are weighted by user actions (interaction);
- the likelihood of a tf-idf interaction response from a vacancy and resume specialization (a meta-attribute on logistic regression);
- the distance between the texts of the vacancy and resume;
- DSSM by job title and resume title (meta-sign on neural network).
A good result shows that a certain number of responses and invitations per day can be extracted from this direction with the same marketing costs.
For example, it is known that with a large number of signs in a logistic regression, the probability of retraining increases.
Suppose we use tf-idf vectorizer for texts of CVs and vacancies with a dictionary of 10 thousand words and phrases. Then in the case of a quadratic expansion in our logistic regression will be 2 * 10 000 + 10 000² weights. It is clear that with such a sparseness even individual cases can significantly affect each individual weight “in the summary there was a rare word such and such — in a vacancy such and such — the user clicked”.
Therefore, now we are trying to make meta-signs on logistic regression, in which the coefficients of quadratic expansion are compressed using factorization machines. Our 10,000² weights are represented as a matrix of latent vectors of dimension, for example, 10,000x150 (where we chose the dimension of the latent vector 150 ourselves). In this case, individual cases of compression cease to play a large role, and the model begins to better take into account more general patterns, and not to memorize specific cases.
We also use meta-signs on the DSSM neural networks, which we have already written about , and on ALS, which we also wrote about , but in a simplified way. In total, the introduction of meta-signs to date has given us (and our customers) more than 44 thousand additional responses (leads) to vacancies per day.
As a result, the simplified model stacking scheme in vacancy recomendations has now become:

Thus, stacking in production makes sense. But this is not the automatic, combinatorial stacking. We make sure that the models on the basis of which meta-attributes are created remain simple and use the existing data and the calculated static features to the maximum extent. Only in this way can they remain in production without gradually becoming an unsupported black box, and remain in a state where they can be retrained and improved.
