Why does Feistel's network work? Fingers explanation

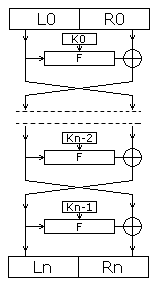
In the continuation of the article about blowfish, I would like to talk about its basis - the Feistel network . People "in the subject" have heard about it more than a hundred times - this network is used in the vast majority of block ciphers. But here you are, honestly, is anything clear from the picture on the right? Well, let's say one way (encryption) is understandable, but vice versa?
If not, then I ask for a mat.


First, at least run a quick tour of Wikistake to understand in general terms what it is about.

For simplicity, we will work with a block consisting of only two bytes. As stated in Wikipedia , it must call drank half and the left side L , and right R . May it be so.

And so, we have two halves of the block, and the mysterious function F. Let's go

• The first thing we need to learn is that XOR (denoted by ⊕ ) is an involutive operation. Do not kick, it just means that if you double one number with another, then again we get the desired. Those. A ⊕ B ⊕ B == A.
  It follows that it is possible to build endless chains A ⊕ B ⊕ C ⊕ D ⊕ ... and if we redirect everything in the opposite order, we get A.
  For example, ((100 ⊕ 200) ⊕ 50) ⊕ 150 = 8. Hence, 8 ⊕ 150 ⊕ 50 ⊕ 200 = 100
• The second important point is that at one moment in time only one half of the block changes
• Now about the “black box” or function F. In principle, function F can be any made-up function (albeit a complex hash, at least stupidly returning 0), because when we reverse everything (decrypt) in the reverse order, we always have the second argument The result of this function will be the same as in the encryption process. In practice, its creation is akin to art and does not give a 100% guarantee against new methods of cryptanalysis.

How does this “same” come about?

Consider the example of three rounds in steps

Encryption

0) We have L and R some numbers. Let them be 100 and 200. and F , some kind of function depending on L and round number n. Let, for example, F simply add them modulo 256 (so that it does not crawl out byte). Those. F (L, n) = (L + n)% 256. (% is the remainder of the division)

Round one (n = 1)
1) We take R (200) and Xorim it with the result of the function F (L, n), t .e. 200 ⊕ ((100 + 1)% 256) we get 173 .
2) We put 173 in place of L, and in place of R the previous value of L (100), i.e. swap R and the result of the Xor R with function F.

Round 2 (n = 2)
1) Now L = 173, R = 100. Xorim 100 c ((173 + 2)% 256), we get 203
2) Put 203 in place L, and 173 in place of R.

Round 3 (n = 3)
1) L = 203, R = 173. Xorim 173 c ((203 + 3)% 256), we get 99
2) Since the round is last, we only change R (so that we don’t do the rearrangement later)

After encryption L = 203, R = 99.

Decryption

We go in the reverse order, the round numbers go from 3 to 1

Round 1 (n = 3)
1) L = 203, R = 99. Xorim 99 s ((203 + 3)% 256) we get 173 . A familiar number?
2) Put 173 in place of L, 203 in place of R

Round 2 (n = 2)
1) L = 173, R = 203. Hence, 203 ⊕ ((173 + 2)% 256) = 100 . Almost!
2) Change L = 100, R = 173

Round 3 (n = 1)
1) L = 100, R = 173. We consider R (permutation, as in the case of encryption, is not needed) = 173 ⊕ ((100 + 1 )% 256) = 200 URAAAA !!!

L = 100, R = 200. As in a pharmacy)

That is, the entire Feistel network essentially boils down to an alternate ksorboth halves of the block with some calculated values, which are substituted in the reverse order during encryption .

And finally, the java code that implements the algorithm described above.

public class BlockTest
{
    private static int rounds = 3;
    public void feist (int [] a, boolean reverse)
    {
        int round = reverse? rounds: 1;
        int l = a [0];
        int r = a [1];
        for (int i = 0; i <rounds; i ++)
        {
            if (i <rounds - 1) // if not the last round
            {
                int t = l;
                l = r ^ f (l, round);
                r = t;
            }
            else // last round
            {
                r = r ^ f (l, round);
            }
            round + = reverse? -eleven;
        }
        a [0] = l;
        a [1] = r;
    }
    private int f (int b, int k)
    {
        return b + k;
    }
    public void test ()
    {
        int [] a = new int [2];
        a [0] = 100;
        a [1] = 200;
        feist (a, false);
        feist (a, true);
    }
}

I hope you enjoyed it;)