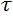Operational Amplifiers (based on the simplest examples): Part 2

Instead of boring entry

Last time I tried to briefly explain the basic principles of operation of operational amplifiers. But I just can’t refuse a request to continue the topic. This time, the schemes are a little more complicated, but I will try not to stretch the tedious mathematical conclusions.

Integrators and differentiators

Imagine that you have to consider the voltage integral. Scary, isn't it? And who needs this at all?
So, for these purposes, an integrator is needed .
In the general case (for an ideal operative) this option is considered:

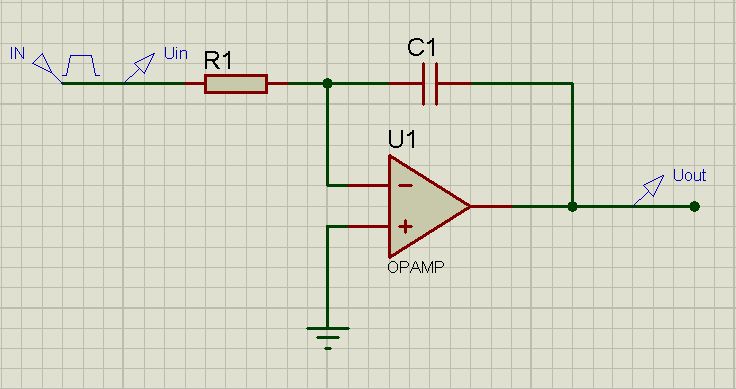
Further, I strongly recommend a little work up and a little bit of physics and higher mathematics. Although, this is not absolutely necessary.

Remember the capacitor charge formula?

Given that the charge will change in time, we can safely assume:

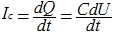
Next ... A non-inverting input is connected to ground. The voltage across the capacitor equals the opposite voltage at the output, in other words
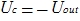. It means that

Further, solving and integrating, we obtain the (almost) final formula:

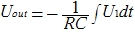
This is, so to speak, in general form. As a result, I want to draw attention to the fact that the output voltage plays an essential role for each moment in time t. We will take it as a free element:

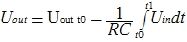
It is logical to assume that the integration is in time from t0 to t1.

Here's the problem for you. The capacitor is discharged. The output voltage is zero. The circuit is off. The capacitor has a capacity of 1 μF. 30k ohm resistor The input voltage is first -2V, then 2V. The polarity changes every second. In other words, we applied a pulse generator to the input.
So, we decide. Putting together a quick scheme in Proteus. Draw a graph. We enter the input and output voltages as functions. Click "Simulate the schedule." We get:

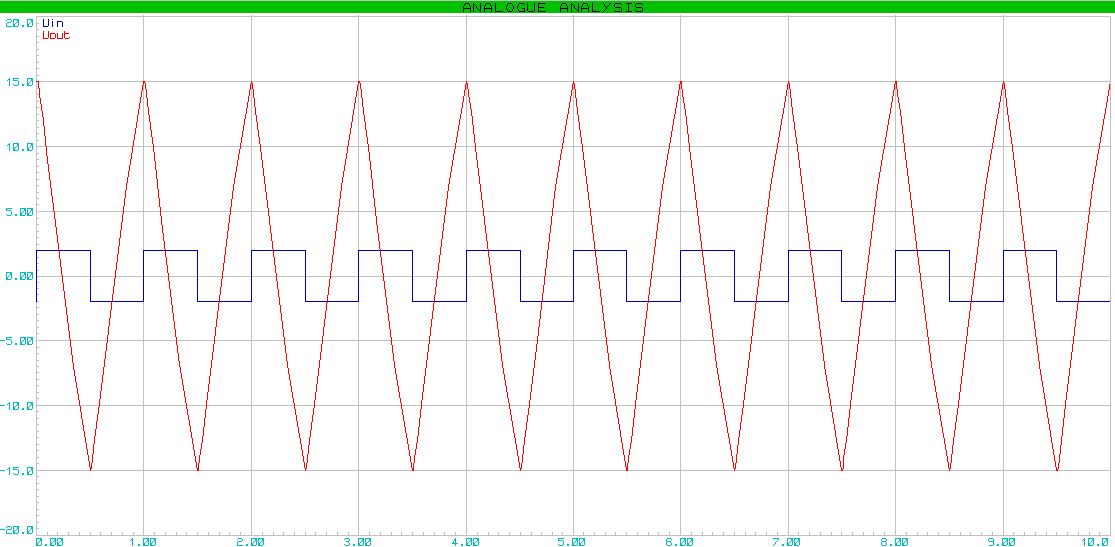
A “sawtooth” signal came out. Please note that the capacitor affects the sharpness of the decline. It should fluctuate within reasonable limits in order to have time to charge / discharge, and not to discharge / discharge * too quickly. By the way, it would be logical to assume that the signal is amplified within the power supply of our op-amp.

Next, we move on to differentiators .
It is no more complicated than in integrators.
Differentiator:

And here is the analog calculation formula:

And again the boring formulas ... The
current through the capacitor is equal.

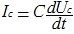
Since the operational amplifier is close to ideal, we can assume that the current through the capacitor is equal to the current through the resistor.
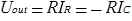, which means, if we substitute the current value, we get:


As in the previous example, consider a more practical example. 50μF capacitor. 30k ohm resistor At the entrance we serve a “saw”. (Honestly, in the proteus it was not possible to make a saw using standard tools, I had to resort to the Pwlin tool.
As a result, we get the graph:


To summarize.
Integrator. "Rectangle" -> "Saw"
Differentiator. "Saw" -> "Rectangle"
PS Differentiators and integrators will be considered later in a completely different guise.

Comparators

A comparator is a device that compares two input voltages. The state at the output changes stepwise depending on which voltage is greater. There is nothing special, just give an example. At the first input, we supply a constant voltage equal to 3V. At the second input - a sinusoidal signal with an amplitude of 4V. We remove the voltage from the output.

The graph contains comprehensive information that does not need comments:

Logarithmic and exponential amplifiers

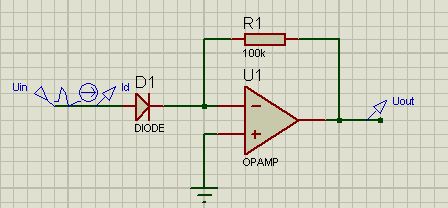
To obtain a logarithmic characteristic, an element with it is needed. For such purposes, a diode or transistor is quite suitable. In order not to complicate, then we will use a diode.
To begin with, as usual, I’ll give a diagram ...

... and the formula:

Please note that e is the charge of an electron, T is the temperature in Kelvin and k is the Boltzmann constant.
Again, you have to remember the physics course. The current through the semiconductor diode can be described as:
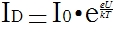(the image did a little more, because the degree of the formula was “crooked”)
Here U is the voltage on the diode. I0 is the leakage current at a small reverse bias. Prologarithm and get:

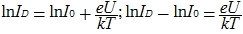
From here we get the voltage on the diode (which is identical to the voltage at the output):

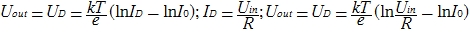
It is worth making a note that at a temperature of 20 degrees Celsius:

Let's check how this scheme works graphically. Run the proteus. Set the input signal: The

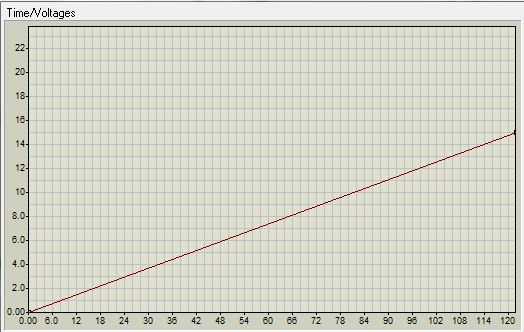
current on the diode will change as follows:

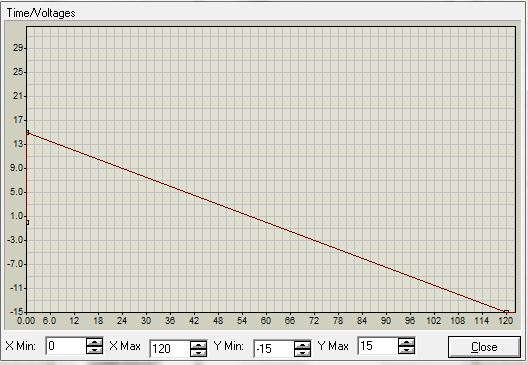
The output voltage changes according to the logarithmic law:


The next item is the exponential amplifier, I will leave it without comment. I hope everything will be clear here.

Instead of a conclusion

In this part, I tried to reduce the mathematical conclusions to a minimum, and to focus on practical application. I hope you enjoyed it :-)

* UPD .: The capacitor charge / discharge time is defined as:, 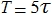where 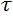is the transient time. The formula is valid for the RC circuit 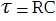. During T, the capacitor will be fully charged / discharged by 99%. Sometimes time is used for calculations 3