H #, create your own programming language

Good day.
In this article I want to review one of the main innovations in Visual Studio 2010, namely, the functional programming language F #.

We will consider the syntax and potential of F # using the example of creating our own interpreter for the programming language that we invented (after all, talking about something is always more interesting with examples).

We describe the task that we are going to solve, namely, the syntax of our programming language, it will be quite simple, here's what we want to see: So, we have support for functions with parameter passing and return value, printing, arithmetic operations and local variables. We’ll start to implement this, for this we need to install an additional package F # Power Pack

function Summ(a,b,c)
{
    val d = a+b+c;
    print d;
    return d;
}

function MyEvaluations(a,b,c)
{
    val in = Summ(a,b,1);
    val out = Summ(b,c,1);
    val d = in*out;
    return d;
}

function Program()
{
    print(MyEvaluations(1,2,3));
}

from here

Vocabulary

Now we create a new F # project from the F # Parsed Language Starter online template and clear all files except lexer.fsl.
In order to deal with the contents of this file, let's first analyze our language by bones. By the word "token", we understand the minimum bricks of which the programming language consists.
Tokens include keywords, brackets, commas, names, in general, everything that the program source code consists of. At the level of tokens, we do not have functions and other logical units.

Let's open the lexer.fsl file.
In F #, the keyword module is the analogue of the namespace, the open keyword is the analogue of using, so the first thing we will write now is to determine the area in which we work:

{
module Lexer
open System
open Parser
open Microsoft.FSharp.Text.Lexing

let lexeme lexbuf =
    LexBuffer.LexemeString lexbuf
}
let digit = ['0'-'9']
let whitespace = [' ' '\t' ]
let newline = ('\n' | '\r' '\n')
let symbol = ['a'-'z''A'-'Z']

Variables in F # are declared using the let keyword, also, we can use regular expressions here.
So, we remove all the code below the line

rule tokenize = parse

which is a service marker, indicating that the description of our language will go below, and insert the following code: Since this file will be processed by additional means of the PowerPack library, the F # code in this file itself is surrounded by the first block of curly brackets. This is the easiest part, here we just write the string constants or regular expressions that are present in our language, we will have few of them: arithmetic operators, brackets, three keywords, a comma and a semicolon.

| whitespace { tokenize lexbuf }
| newline     { tokenize lexbuf }

// Operators
| "+" { PLUS }
| "-" { MINUS }
| "*" { MULTIPLE }
| "/" { DIVIDE }
| "=" { EQUALS }

// Misc
| "(" { LPAREN }
| ")" { RPAREN }
| "," { COMMA }
| ";" { ENDOFLINE }
| "{" { BEGIN }
| "}" { END }

// Keywords
| "function" { FUNCTIONKW }
| "return" { RETURN }
| "var" { VARIABLE }

Next, using regular expressions, we will train our interpreter to “pull out” the numbers and names of variables / functions from the code. In fact, at this stage we turned our plain text code into such a sequence of objects: Each object has its own type, which is indicated in the example above. However, the DECIMAL and NAME objects must also have a value. To do this, write the following lines: You can interpret this as a call to the constructor. All that is in braces is our data types. After processing, the program text will be a sequence of objects of these types. eof - service token that signals the end of the parsed text

FUNCTIONKEYWORD NAME LPAREN NAME COMMA NAME COMMA NAME RPAREN
BEGIN
VARIABLE NAME EQUALS NAME PLUS NAME PLUS NAME ENDOFLINE
…..

| digit+('.'digit+)? { DECIMAL(Double.Parse(lexeme lexbuf)) }
| symbol+ { VARNAME(String.Copy(lexeme lexbuf)) }

| eof { EOF }

Parsing

To make it a little clearer where the data types came from, and why NAME has string content and DECIMAL is numerical, open the Parser.fsy file and paste the following code into it:

%{
open ParserLibrary
open System
%}

%start start

%token DECIMAL
%token PLUS MINUS MULTIPLE DIVIDE
%token LPAREN RPAREN
%token FUNCTIONKW RETURN VARIABLE
%token BEGIN END
%token EQUALS
%token VARNAME
%token ENDOFLINE
%token COMMA
%token EOF
%type start

%%


All our data types are indicated here, if our type must have a value, then the type of this value is written in angle brackets.
start is the so-called “grammar axiom”, something that we will try to “collect” when interpreting our code.

The grammar is written in the following form:

ТипДанных: | Первый возможный набор состовляющих | Второй возможный набор состовляющих | … | …

The first line will look like this:

start: | WholeProgram

This indicates that the purpose of our analysis is to get the "whole program". The
"whole program" in our closer examination is just a list of functions.
Therefore, we write this fact:

WholeProgram:
| FunctionDescription
| WholeProgram FunctionDescription

It is worth noting a rather unusual form of forming lists in this form of recording, the fact is that the number of "components" for each element must be fixed, and in order not to limit the number of possible functions in our language, we go for such a trick. When the system finds the first function - it creates a WholeProgram object from it, when it sees the second function - we have WholeProgram (from the first function) and FunctionDescription (second function) next to us, and the system collapses both of these objects into a new WholeProgram, thus removing the restriction on the total number of functions in the program text.
If we illustrate the grammar, we get about the following picture:

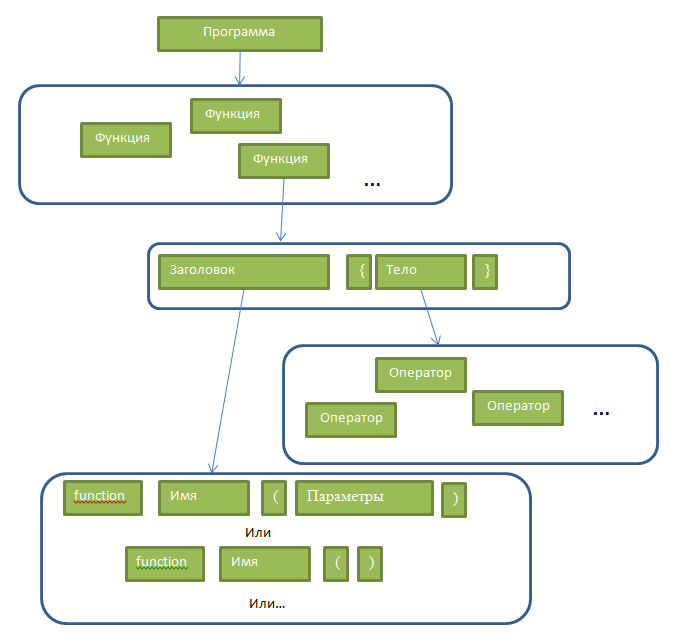
Now we will write down what the function is:

FunctionDescription:
| FunctionKeyWord FunctionTitle Begin End
| FunctionKeyWord FunctionTitle Begin OperatorsList End

We could restrict ourselves only to the second version of the representation, but in this case empty functions would lead to an error in the interpreter, as can be seen from the code, the function consists of a keyword, a header, curly braces and, possibly, a set of operators inside a function - its body.
The function header consists of its name, parentheses and, possibly, a list of parameters: AdditionParametersList and OperatorsList objects are lists and therefore are defined similarly to WholeProgram: The operator is one line of our program inside the function body, let there be two options in our language: Which corresponds for example the lines:

FunctionTitle:
| VarName LParen RParen // Функция без параметров
| VarName LParen VarName RParen // Функция с одним параметром. Так как параметры разделяются запятыми, то нам проще будет вынести вариант без запятых отдельно
| VarName LParen VarName AdditionParametersList RParen // Функция с множеством параметров

OperatorsList:
| Operator
| OperatorsList Operator

AdditionParametersList:
| Comma VarName
| AdditionParametersList Comma VarName

Operator:
| VaribaleKeyWord VarName Equals Expression EndOfLine
| ReturnKeyWord Expression EndOfLine

val d = in*out;
return d;

Initially, we defined 4 arithmetic operations, taking into account that multiplication and division are more priority operations than addition and subtraction: Such a division will allow us to parse the expression 2 + 2 * 2 as Expression Plus HighExpression, and then deploy HighExpression in a separate subtree: Expression Plus (HighExpression MULTIPLY Operand), which will correctly handle the priority of operations. At the bottom level, the operand we can have is either a number, the name of an existing variable, the name of a function, or (if we want) an expression in parentheses. Let us return to our F # (now in its pure form) and consider such a possibility as constructors with pattern matching, namely, we will describe the data types just used

Expression:
| Expression PLUS HighExpression
| Expression MINUS HighExpression
| HighExpression // Так как в определении "Operator"'а у нас фигурирует только Expresson, необходимо учесть возможность отсутствия сложения и вычитания и "провалиться" на уровень ниже.
HighExpression:
| HighExpression MULTIPLY Operand
| HighExpression DIVIDE Operand
| Operand // Аналогично, в случае отсутствия умножения и деления - работаем сразу с переменными.

Operand:
| DECIMAL
| VarName
| FunctionTitle
| LParen Expression RParen // Возвращаясь к Expression мы создаём своего вида рекурсию, позволяющую обрабатывать неограниченную вложенность скобок.

namespace ParserLibrary
open System

type Operator = 
    | VarOperator    of string * Expression
    | ReturnOperator of Expression

and Operand = 
    | DECIMALOP   of Double
    | SUBEXPROP   of Expression
    | VARNAMEOP   of String
    | FUNCOP      of FunctionTitle

and HighExpression =
    | MULTIPLY  of HighExpression * Operand
    | DIVIDEOP  of HighExpression * Operand
    | VAR       of Operand

and Expression =
    | SUMM            of Expression * HighExpression
    | SUB             of Expression * HighExpression
    | HighExpression  of HighExpression
       
and FunctionTitle = String * List
and FunctionDescription = FunctionTitle * OperatorsList
and OperatorsList = List
and AdditionParamsList = List
and WholeProgram = List

In fact, we declared 9 objects, each of which has several named constructors with different parameters (in fact, such a set of constructors is similar to union in C ++).
Note that the asterisk "*" in this context is not a multiplication, but a parameter separator, that is, . a constructor named VarOperator for type Operator takes a string (string) and expression (expression)
All we have to do to complete the first part of writing our interpreter is to connect these data types in the Parser.fsy file, for this, opposite each condition in curly brackets we write the corresponding constructor
It will look like this: $ 1, $ 2, etc. Is the number of the variable in the condition

start: WholeProgram { $1 }

WholeProgram:
| FunctionDescription { $1 :: [] }
| WholeProgram FunctionDescription { $1 @ ($2 :: []) }

FunctionTitle:
| VARNAME LPAREN RPAREN { $1, [] }
| VARNAME LPAREN VARNAME RPAREN { $1, $3 :: [] }
| VARNAME LPAREN VARNAME AdditionParamsList RPAREN { $1, $3 :: $4 }

AdditionParamsList:
| COMMA VARNAME { $2 :: [] }
| AdditionParamsList COMMA VARNAME { $1 @ ($3 :: []) }

OperatorsList:
| Operator { $1 :: [] }
| OperatorsList Operator { $1 @ ($2 :: []) }

FunctionDescription:
| FUNCTIONKW FunctionTitle BEGIN END { $2, [] }
| FUNCTIONKW FunctionTitle BEGIN OperatorsList END { $2, $4 }

Operator:
| VARIABLE VARNAME EQUALS Expression ENDOFLINE { VarOperator($2, $4) }
| RETURN Expression ENDOFLINE { ReturnOperator($2) }

Expression:
| Expression PLUS HighExpression { SUMM($1, $3) }
| Expression MINUS HighExpression { SUB($1, $3) }
| HighExpression { HighExpression $1 }

HighExpression:
| HighExpression MULTIPLE Operand { MULTIPLY($1, $3) }
| HighExpression DIVIDE Operand { DIVIDEOP($1, $3) }
| Operand { VAR $1 }

Operand:
| DECIMAL { DECIMALOP($1) }
| VARNAME { VARNAMEOP($1) }
| FunctionTitle { FUNCOP($1) }
| LPAREN Expression RPAREN { SUBEXPROP($2) }

Using this code as an example, we’ll introduce another great feature of F # - work with lists.
The expression A :: B means creating and returning a new list based on list B with the addition of the element A
[] - an empty list
. We can also specify lists in the code directly or from ranges, for example:
[1,2,3,4, 5] or [1..5]
In this case, 100 :: [1..5] will return the following list to us: [100,1,2,3,4,5]
The @ operator - creates a new list from the union of two existing ones .
For example: [1..5] @ [6..10] will return [1..10]

Note that in the case of a selection by template - we specify a named constructor, for the same types that are simply synonymous with some tuples (FunctionDescription, OperatorsList, etc.) - we simply list the parameters in the order we declared in tuple.
So, this is all we need in order for F # to make us a parsing tree from plain text, the second part is interpretation.
Open the Program.fs file and write open for those namespaces that we will use:

open System
open Microsoft.FSharp.Text.Lexing
open System.Collections.Generic;
open ParserLibrary
open Lexer
open Parser

Interpretation

Further, for interpretation, we will need to have a list of functions (or better, a dictionary), named stacks for each function (so that there are no conflicts of variable names) and the name of the function currently being executed.
To do this, we declare variables using the already familiar keyword let: In classical functional programming, all objects are immutable, this can be seen in the example of working with lists, when instead of adding an item to the list, we create a new one based on existing ones. This allows you to seamlessly parallelize programs, because No need to have complex syncs to write.

let stack = Dictionary>()
let functionsList = Dictionary()
let mutable currentFunctionName = "Program";

F #, being a functional language, perfectly supports the entire .NET library, allowing you to work with mutable objects. Full copying of data in this case does not occur, only references to objects are copied, this allows you to achieve a compromise in speed without breaking the ability to beautifully parallelize data, a kind of copy on write, if you want.

So, let's get into the interpretation:
Let's start by parsing an expression. We will
declare a function with a selection by template, let rec are keywords, EvaluateExpression is a name, expression is a parameter.
Recall that when declaring types we created constructors with a choice by template, we use the same templates when choosing a branch for executing a function. For example: if the passed parameter expression was created using the SUMM (expression, highExpression) constructor, then we execute the addition branch, etc.
You may notice that this function practically repeats the constructors created earlier, attributing a certain action to each of them. Since we introduced support for variables and functions, we need to write handlers for this case. In the case of variables, everything is more or less simple, we go to a dictionary containing the values ​​of the variables of the current function and get the value by the name of the variable (remember that VARNAMEOP is associated with the type String)

let rec evaluateExpression expression =
    match expression with
    | SUMM (expr, hexpr)    -> (evaluateExpression expr) + (evaluateHighExpression hexpr)
    | SUB (expr, hexpr)     -> (evaluateExpression expr) - (evaluateHighExpression hexpr)
    | HighExpression hexpr  -> evaluateHighExpression hexpr
 
 and evaluateHighExpression highExpression =
    match highExpression with
    | MULTIPLY (hexpr, oper)  -> (evaluateHighExpression hexpr) * (EvaluateOperand oper)
    | DIVIDEOP (hexpr, oper)  -> (evaluateHighExpression hexpr) / (EvaluateOperand oper)
    | VAR oper                -> EvaluateOperand oper

 and EvaluateOperand oper =
    match oper with
    | DECIMALOP x -> x
    | VARNAMEOP x -> stack.Item(currentFunctionName).Item(x)
    | FUNCOP x    -> evaluateFunction x
    | SUBEXPROP x -> evaluateExpression x

In case of contact with a function, we need to copy the parameters from the calling function in accordance with the function header and start its execution.
To do this, we add the following code: This is also a function, but not with a choice by template, but in a more familiar form for us. Let's analyze the pipeline operator “|>”, in fact, this is a more understandable way to call chains of functions, if earlier we needed to write OuterFunction (InnerFunction (Validate (data))), then in F # we can “expand” this chain: data |> Validate |> InnerFunction |> OuterFunction Both records produce the same result, however, when using the “|>” operator, we use functions from left to right, in case of long chains it is more convenient.

and evaluateFunction(f:FunctionTitle) =
    let caller = currentFunctionName;
    let newStack = Dictionary()
    let realParams = functionsList.Item (f |> GetFunctionName) |> GetFormalParamsListDecription

    let formalParams = GetFormalParamsListTitle(f)
    ignore <| List.mapi2 (fun i x y -> newStack.Add(x, stack.Item(caller).Item(y))) realParams formalParams
    
    currentFunctionName <- GetFunctionName(f)    
    stack.Add(currentFunctionName, newStack)
    
    let operatorsList = functionsList.Item(GetFunctionName f) |> GetOperatorsList
    
    let result =  RunFunction operatorsList

    ignore <| stack.Remove(currentFunctionName)

    currentFunctionName <- caller
    result
// Часть вызываемых здесь функций будет определена чуть позже

The peculiarity of these functions is that we do not need to write return, for example, the
test (a) = a * 10 function
will return a * 10, this is partly convenient, but we need to take care not to return any value “by accident” (to in a word, VS will underline all inadvertent returns), for this we use the ignore method, which does nothing and returns nothing so that all ignore are at the beginning of the line - we use the inverse pipeline operator "<|", it does the same thing and “|>”, only in the opposite direction, now the functions are applied from right to left.
In the case of a simple assignment, in order to avoid returning the value, instead of “=” the operator “<-“ is used.

We will analyze the line in more detail:

ignore <| List.mapi2 (fun i x y -> newStack.Add(x, stack.Item(caller).Item(y))) realParams formalParams

The List class contains a set of mapi * methods (for a different number of lists), the essence of these methods is that they process several lists (in our case 2) in parallel, passing the number of the element in both lists and the elements themselves to the handler function under the assumption that the lengths lists are equal. The mapi2 method accepts 3 parameters, a handler function and two processed lists.
For example, as a result of executing the following code: We will get the result: 16 27 38 49 60 Since the order of the parameters in brackets is the same when calling a function and when describing it in our language, we simply process the elements from the call lists and function declarations in pairs.

let firstList = [1..5]
let secondList = [6..10]
ignore <| List.mapi2 (fun i x y -> Console.WriteLine(10*x+y)) firstList secondList

The fun keyword defines a new function (we can draw an analogy with lambdas in C #), which we will use to process lists, our function takes 3 parameters, i is the number of the current element in both lists, x and y are elements from the first and second lists, respectively .
So here we are copying into our new stack a variable from the stack of the calling function.

After preparing the parameters, we call the function, remember the result, delete the dictionary (stack) and restore the name of the calling function. Because return is not necessary to write, then to return the value just write the name of the variable that we want to return. Now we write the runFunction method:

 let result =  RunFunction operatorsList

    ignore <| stack.Remove(currentFunctionName)

    currentFunctionName <- caller
    result

and RunFunction(o:OperatorsList) =
    ignore <| List.map (fun x -> EvaluateOperator x) o
    stack.Item(currentFunctionName).Item("return")

The List.map method iterates over all elements of the list, then we simply return the resulting variable from our current stack. There are only 2 types of operators in our language, this is either a variable declaration or a return value, in both cases we calculate the value and add it to the dictionary (stack), in case of return we use the fact that return in our language is a keyword and we can safely use it for your own purposes without fear of conflict with an already declared variable. Since we want to use a couple of predefined functions in our language, to perform I / O, we add a few checks: We check the name of the function and, depending on the result, either print the value of the variable or read the value from the keyboard.

and EvaluateOperator operator =
    match operator with
    | VarOperator (name, expr) -> stack.Item(currentFunctionName).Add(name, evaluateExpression expr)
    | ReturnOperator expr      -> stack.Item(currentFunctionName).Add("return", evaluateExpression expr)

and RunFunction(o:OperatorsList) =
    if currentFunctionName.Equals "print" then
        stack.Item(currentFunctionName).Add("return", 0.0)
        Console.WriteLine(stack.Item(currentFunctionName).Item("toPrint").ToString())
    if currentFunctionName.Equals "get" then
        Console.Write("Input: ");
        stack.Item(currentFunctionName).Add("return", Double.Parse(Console.ReadLine()))
    if currentFunctionName.Equals "Program" then
        stack.Item(currentFunctionName).Add("return", 1.0)

    ignore <| List.map (fun x -> EvaluateOperator x) o
    stack.Item(currentFunctionName).Item("return")

In order not to write in the main return method, we define specials. a variable even before the function body is executed.

Significant indentation is used in F #, in particular, to highlight the body of if blocks.
The last thing we need to do is to identify the missing functions that we used and write a shell that our parser will use: Since we declared some types simply synonyms, after the word with there is no constructor name, just an enumeration of all parameters, after the arrow is the body of the function, in this case we just write the name of the variable to be returned. If writing a function call without parentheses is unusual for you, F # allows you to write code in this form: These entries are absolutely equivalent.

let GetFunctionName f = match f with name, foo -> name
let GetFunctionNameDescription f = match f with t, foo -> GetFunctionName t
let GetFormalParamsListTitle t = match t with foo, paramerers -> paramerers
let GetFormalParamsListDecription f = match f with t, foo -> GetFormalParamsListTitle t   
let GetOperatorsList f = match f with foo, o -> o
let GetTitle f = match f with t, too -> t

let GetFunctionName(f) = match f with name, foo -> name
let GetFunctionNameDescription(f) = match f with t, foo -> GetFunctionName(t)
let GetFormalParamsListTitle(t) = match t with foo, paramerers -> paramerers
let GetFormalParamsListDecription(f) = match f with t, foo -> GetFormalParamsListTitle(t)   
let GetOperatorsList(f) = match f with foo, o -> o
let GetTitle(f) = match f with t, too -> t

Finishing touches

And finally, the last one: We define a new function in which we will try to parse the string entered from the keyboard, if the parsing is successful - we add all the functions from the received list (program) to our functionsList variable. To call a function at the beginning of the program, simply write its name without indentation at the end of the file. Since we have two predefined functions in our language (get and print) - add them, then execute a function called Program. The last thing that can be described in this example is an interesting way of constructing objects for which we did not define constructors through match. If we expect a FunctionTitle object, to create it, just wrap its parameters (String and

printfn "H#"

let mutable source = "";
let rec readAndProcess() =
    printf ":"
    match Console.ReadLine() with
    | "quit" -> ()
    | "GO" ->
        try
            printfn "Lexing..."
            let lexbuff = LexBuffer.FromString(source)
            
            printfn "Parsing..."
            let program = Parser.start Lexer.tokenize lexbuff
            ignore <| List.map (fun x -> functionsList.Add(GetFunctionNameDescription(x),x)) program
            functionsList.Add("print",(("print", ["toPrint"]), []))
            functionsList.Add("get",(("get", []), []))
            printfn "Running..."
            ignore <| (functionsList.Item("Program") |> GetTitle |> evaluateFunction)
            
        with ex ->
            printfn "Unhandled Exception: %s" ex.Message

        readAndProcess()
    | expr ->
        source <- source + expr
        readAndProcess()

readAndProcess()

and FunctionTitle = String * List
and FunctionDescription = FunctionTitle * OperatorsList
and OperatorsList = List
and AdditionParamsList = List
and WholeProgram = List

) in parentheses, indicate the data type is not necessary.

("print",(("print", ["toPrint"]), []))

Launch

Чтож, запустим наш интерпретатор:


После нажатия Enter мы увидим приглашение ввести значение переменной:


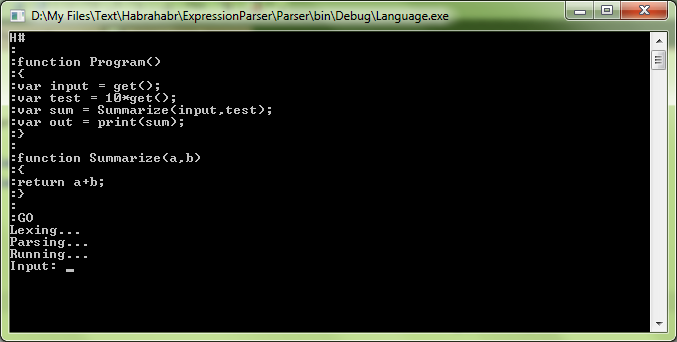
И после этого:


Чтож, программа действительно работает.
Исходный код с бинарниками можно скачать здесь.

Если теперь ещё раз взглянуть на код на F#, то можно увидеть, что мы написали минимум, просто описывающий то, что мы хотим сделать, это позволило написать свой интерпретатор и уложиться всего в ~200 строк кода, F# позволяет избавиться от рутинной работы по написанию кода, который не отвечает на вопрос «что», а отвечает на вопрос «как». Безусловно, программирование на этом языке по началу кажется трудным, но в ряде случаев оно того стоит, так как даёт возможность писать гибкий код, который легко поддерживать.
Спасибо за внимание.