How computers learned how to recognize images amazingly well

Significant scientific work from 2012 transformed the field of image recognition software

Today I can, for example, open Google Photos, write “beach”, and see a bunch of my photos from various beaches that I visited in the last decade. And I never signed my photos - Google recognizes beaches on them based on their content. This seemingly boring feature is based on a technology called “deep convolutional neural network”, which allows programs to understand images using a complex method that was not available to technologies of previous generations.

In recent years, researchers have found that software accuracy becomes better as they build deeper neural networks (NS) and train them on ever larger data sets. This created an insatiable need for computing power, and enriched GPU manufacturers such as Nvidia and AMD. A few years ago, Google developed its own special chips for the National Assembly, while other companies are trying to keep up with it.

At Tesla, for example, Andrei Karpati, a deep learning expert, has been appointed head of the Autopilot project. Now the automaker is developing its own chip to accelerate the work of the NS in future versions of the autopilot. Or take Apple: the A11 and A12 chips central to the latest iPhone have a “ neural processor”"The Neural Engine, which speeds up the work of the NS and allows applications for image and voice recognition to work better. The

experts I interviewed for this article track the beginning of the deep learning boom to a specific job: AlexNet, named after the main author, Alex Krizhevsky." I think that 2012 was a landmark year when AlexNet’s work came out, ”said Sean Gerrish, an MO expert and author of How Smart Cars Think .

Until 2012, deep neural networks (GSS) were a bit of a backwater in the world of Moscow Region. But then Krizhevsky and his colleagues from the University of Toronto took part in the prestigious competition for image recognition, and their program radically surpassed in accuracy everything that was developed before it. Almost instantly, STS became the leading technology in image recognition. Other researchers using this technology soon showed further improvements in recognition accuracy.

In this article, we will delve into deep learning. I will explain what NS is, how they are trained, and why they require such computing resources. And then I will explain why a certain type of NS - deep convolution networks - understand images so well. Do not worry, there will be many pictures.

A simple example with one neuron

The concept of "neural network" may seem vague to you, so let's start with a simple example. Suppose you want the National Assembly to decide whether to drive a car based on the green, yellow and red traffic signals. NS can solve this problem with a single neuron.



A neuron receives input data (1 - on, 0 - off), multiplies by the appropriate weight, and adds all the values ​​of the weights. Then the neuron adds an offset that defines the threshold value for the "activation" of the neuron. In this case, if the output is positive, we believe that the neuron has activated - and vice versa. A neuron is equivalent to the inequality "green - red - 0.5> 0". If it turns out to be true - that is, green is on and red is not on - then the car should go.

In real NS, artificial neurons take another step. By adding up a weighted input and adding an offset, the neuron uses a non-linear activation function. Often a sigmoid is used, an S-shaped function that always yields a value from 0 to 1.

Using the activation function will not change the result of our simple traffic light model (we just need to use a threshold value of 0.5, not 0). But the nonlinearity of activation functions is necessary in order for NSs to model more complex functions. Without the activation function, each arbitrarily complex NS is reduced to a linear combination of input data. A linear function cannot model complex phenomena of the real world. The nonlinear activation function allows the NS to approximate any mathematical function .

Network example

Of course, there are many ways to approximate a function. NS stand out by the fact that we know how to “train” them using a little algebra, a bunch of data and a sea of ​​computing power. Instead of directly programming the NS for a specific task, we can create software starting with a fairly general NS, studying a bunch of marked up examples, and then changing the NS so that it will give the correct label for as many examples as possible. The expectation is that the final NS will summarize the data and will produce the correct labels for examples that were not previously in the database.

The process leading to this goal began long before AlexNet. In 1986, a trio of researchers published a landmark workon backpropagation - a technology that helped make the mathematical training of complex NSs a reality.

To imagine how backpropagation works, let's look at a simple NS described by Michael Nielsen in his excellent online GO textbook . The purpose of the network is to process the image of a hand-written number in a resolution of 28x28 pixels and correctly determine whether the number 0, 1, 2, etc. is written.

Each image is 28 * 28 = 784 input quantities, each of which is a real number from 0 to 1, indicating how much the pixel is light or dark. Nielsen created the NA of this kind:



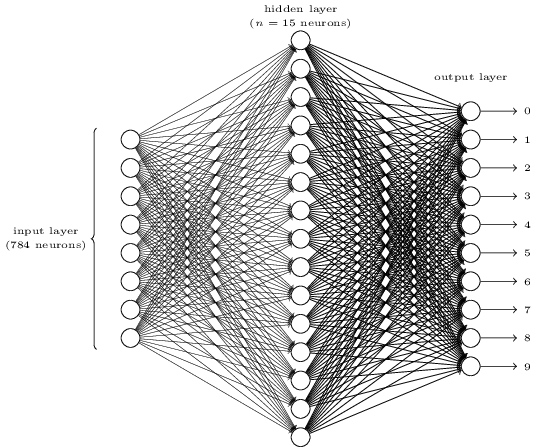
Each circle in the center and in the right column is a neuron similar to the one we examined in the previous section. Each neuron takes a weighted average of the input, adds an offset, and applies an activation function. The circles on the left are not neurons; they represent the network input. And although the picture shows only 8 input circles, in fact there are 784 of them - one for each pixel.

Each of the 10 neurons on the right should “trigger” its own number: the top one should turn on when a handwritten 0 is input (and only in this case), the second one when the network sees a handwritten 1 (and only it), and so on.

Each neuron perceives input from each neuron of the previous layer. So each of the 15 neurons in the middle receives 784 input values. Each of these 15 neurons has a weight parameter for each of the 784 input values. This means that only this layer has 15 * 784 = 11 760 weight parameters. Similarly, the output layer contains 10 neurons, each of which receives input from all 15 neurons of the middle layer, which adds another 15 * 10 = 150 weight parameters. In addition, the network has 25 displacement variables — one for each of the 25 neurons.

Neural network training

The goal of the training is to fine-tune these 11,935 parameters to maximize the likelihood that the desired output neuron - and only it - is activated when the networks give an image of a handwritten digit. We can do this with the well-known set of images MNIST, where there are 60,000 marked images with a resolution of 28x28 pixels.


160 of the 60,000 images from the MNIST set

Nielsen demonstrates how to train a network using 74 lines of regular python code - without any libraries for MO. Learning begins by choosing random values ​​for each of these 11,935 parameters, weights and offsets. Then the program goes through examples of images, going through two stages with each of them:

1. The forward propagation step computes the network output based on the input image and current parameters.
2. The backpropagation step calculates the deviation of the result from the correct output data and changes the network parameters so as to slightly improve its efficiency in this image.

Example. Suppose the network received the following picture:



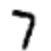
If it is well calibrated, then pin “7” should go to 1, and the other nine conclusions should go to 0. But, let's say that instead, the network at output “0” gives a value of 0.8. It's too much! The training algorithm changes the input weights of the neuron responsible for “0” so that it becomes closer to 0 the next time this image is processed.

For this, the backpropagation algorithm computes an error gradient for each input weight. This is a measure of how the output error will change for a given change in input weight. Then the algorithm uses the gradient to decide how much to change each input weight — the larger the gradient, the stronger the change.

In other words, the learning process “trains” the neurons of the output layer to pay less attention to those inputs (neurons in the middle layer) that push them to the wrong answer, and more to those inputs that push in the right direction.

The algorithm repeats this step for all other output neurons. It reduces the input weights for the neurons “1”, “2”, “3”, “4”, “5”, “6”, “8” and “9” (but not “7”) in order to lower the value of these output neurons. The higher the output value, the greater the gradient of the output error with respect to the input weight - and the more its weight will decrease.

And vice versa, the algorithm increases the weight of the input data for output "7", which makes the neuron produce a higher value the next time it is given this image. Again, inputs with larger values ​​will increase weights more, which will make the output neuron “7” pay more attention to these inputs next time.

Then the algorithm should perform the same calculations for the middle layer: change each input weight in a direction that will reduce network errors - again, bringing output “7” closer to 1, and the rest to 0. But each middle neuron has a connection with all 10 days off, which complicates matters in two aspects.

Firstly, the error gradient for each average neuron depends not only on the input value, but also on the error gradients in the next layer. The algorithm is called backpropagation because the error gradients of the later layers of the network propagate in the opposite direction and are used to calculate the gradients in the earlier layers.

Also, each middle neuron is an input for all ten days off. Therefore, the training algorithm has to calculate the error gradient, which reflects how a change in a certain input weight affects the average error for all outputs.

Backpropagation is an algorithm of climbing a hill: each pass of it brings the output values ​​closer to the correct values ​​for a given image, but only by a little. The more examples the algorithm looks at, the higher it climbs up the hill towards the optimal set of parameters that correctly classify the maximum number of training examples. To achieve high accuracy, thousands of examples are required, and the algorithm may need to cycle through each image in this set dozens of times before its effectiveness stops growing.

Nielsen shows how to implement these 74 lines in python. Surprisingly, a network trained with such a simple program can recognize more than 95% of handwritten numbers from the MNIST database. With additional improvements, a simple two-layer network can recognize more than 98% of the numbers.

Breakthrough AlexNet

You might think that the development of the theme of backpropagation was supposed to take place in the 1980s, and give rise to rapid progress in the MO based on the National Assembly - but this did not happen. In the 1990s and early 2000s, some people worked on this technology, but interest in the National Assembly did not gain momentum until the early 2010s.

This can be tracked by the ImageNet competition.- The annual competition in the MO organized by a computer scientist from Stanford Fay Fey Lee. Each year, rivals are given the same set of more than a million images for training, each of which is manually labeled in categories of more than 1000 - from “fire engine” and “mushroom” to “cheetah”. Participants' software is judged on the possibility of classifying other images that were not in the set. A program can give a few guesses, and its work is considered successful if at least one of the first five guesses matches the mark put down by a person.

The competition began in 2010, and deep NSs did not play a big role in it in the first two years. The best teams used different various MO techniques, and achieved fairly average results. In 2010, the team won with an error rate of 28. In 2011, with an error of 25%.

And then came 2012. A team from the University of Toronto made a bid - later dubbed AlexNet in honor of the lead author, Alex Krizhevsky - and left the rivals far behind. Using deep NS, the team achieved a 16% error rate. For the closest competitor, this figure was 26.

The NS described in the article for handwriting recognition has two layers, 25 neurons and almost 12,000 parameters. AlexNet was much larger and more complex: eight trainable layers, 650,000 neurons and 60 million parameters.

Enormous computing power is required to train NSs of this size, and AlexNet was designed to take advantage of the massive parallelization available with modern GPUs. Researchers figured out how to divide the work of training the network into two GPUs, which doubled the power. And still, despite the tight optimization, the network training took 5-6 days on the hardware that was available in 2012 (on a pair of Nvidia GTX 580 with 3 Gb of memory).

It is useful to study examples of AlexNet's results to understand how serious this breakthrough was. Here is a picture from a scientific work that shows examples of images and the first five guesses of the network by their classification:



AlexNet was able to recognize the tick in the first picture, although there is only a small form in the corner from it. The software not only correctly identified the leopard, but also gave other close options - a jaguar, cheetah, snow leopard, Egyptian Mau. AlexNet tagged the hornbeam photo as “agaric”. Just "mushroom" was the second version of the network.

"Errors" AlexNet are also impressive. She marked the photo with a Dalmatian standing behind a bunch of cherries as “Dalmatian”, although the official label was “cherry”. AlexNet recognized that there was some kind of berry in the photo — among the first five options were “grapes” and “elderberry” - it simply did not recognize the cherry. To a photo of a Madagascar lemur sitting on a tree, AlexNet brought a list of small mammals living on trees. I think that many people (including me) would have put the wrong signature here.

The quality of the work was impressive, and demonstrated that the software is able to recognize ordinary objects in a wide range of their orientations and environments. GNS quickly became the most popular technique for image recognition, and since then the world of MO has not abandoned it.

“In the wake of the success of the 2012 GO-based method, most of the 2013 contestants switched to deep convolutional neural networks,” ImageNet sponsors wrote . In the following years, this trend continued, and subsequently the winners worked on the basis of basic technologies, first applied by the AlexNet team. By 2017, rivals, using deeper NSs, seriously reduced the percentage of errors to less than three. Given the complexity of the task, computers to some extent learned to solve it better than many people.


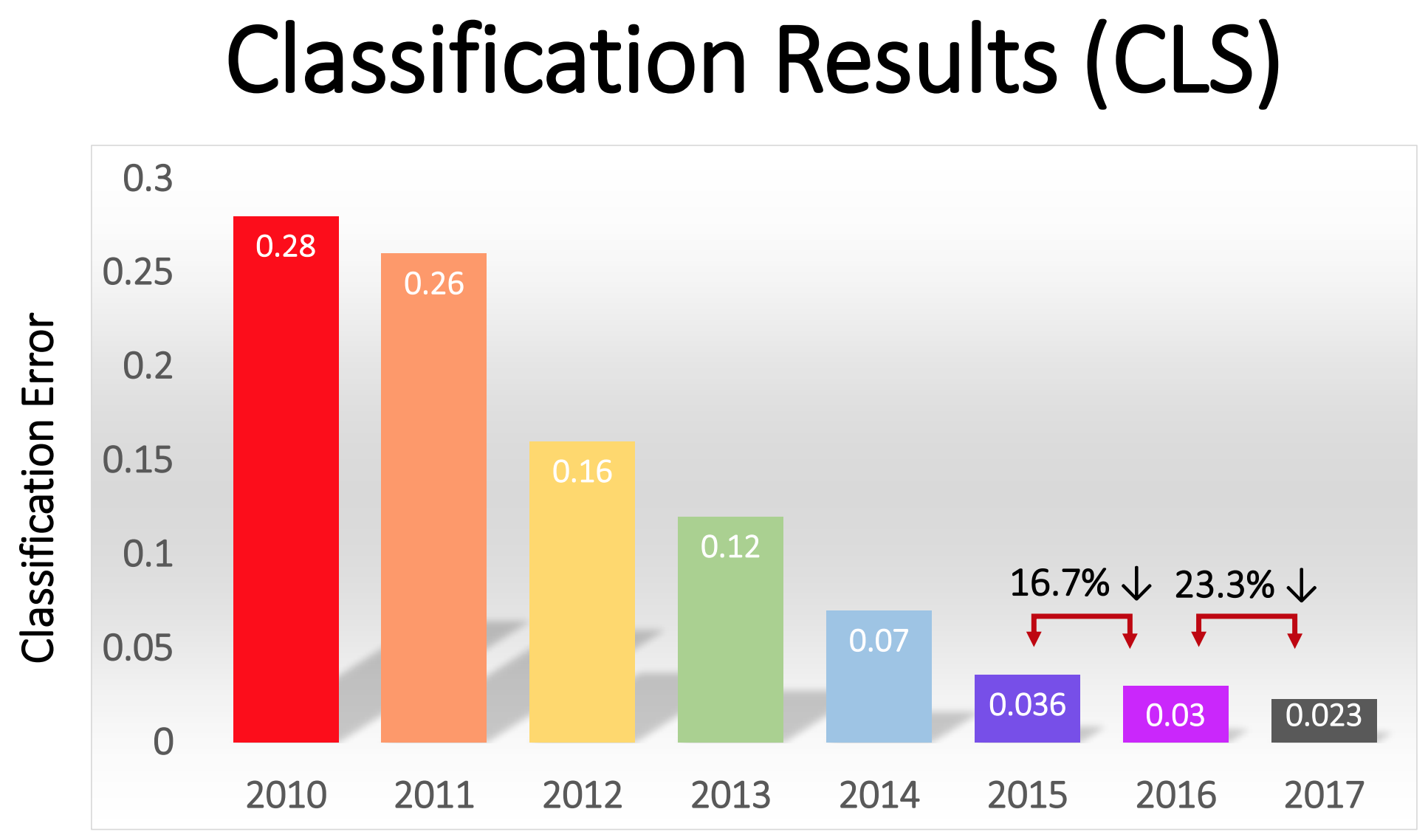
The percentage of errors in the classification of images in different years

Convolution Networks: A Concept

Technically, AlexNet was a convolutional NS. In this section, I will explain what the convolutional neural network (SNA) does, and why this technology has become critical to modern pattern recognition algorithms.

The previously considered simple network for handwriting recognition was completely connected: each neuron of the first layer was an input for each neuron of the second layer. Such a structure works quite well on simple tasks with recognition of numbers in 28x28 pixel images. But it does not scale well.

In the MNIST handwritten digit database, all characters are centered. This greatly simplifies learning, because, say, a seven will always have several dark pixels at the top and right, and the lower left corner is always white. Zero will almost always have a white spot in the middle and dark pixels at the edges. A simple and fully connected network can recognize such patterns quite easily.

But let's say you wanted to create an NS capable of recognizing numbers that can be located anywhere on a larger image. A fully connected network will not work just as well with such a task, since it does not have an effective way to recognize similar features in forms located in different parts of the image. If in your training dataset most of the sevens are located in the upper left corner, then your network will be better at recognizing the sevens in the upper left corner than in any other part of the image.

Theoretically, this problem can be solved by ensuring that your set has many examples of each digit in each of the possible positions. But in practice this will be a huge waste of resources. With increasing image size and network depth, the number of links - and the number of weight parameters - will increase explosively. You will need much more training images (and computing power) to achieve adequate accuracy.

When a neural network learns to recognize a shape located in one place of an image, it must be able to apply this knowledge to recognize the same shape in other parts of the image. SNA provide an elegant solution to this problem.

“It's like you would take a stencil and attach it to all places in the image,” said AI researcher Jai Teng. - You have a stencil with a picture of a dog, and you first attach it to the upper right corner of the image to see if there is a dog there? If not, you are shifting the stencil a bit. And so for the whole image. It doesn't matter where the picture of the dog is. The stencil will match with her. You do not need each part of the network to learn its own classification of dogs. ”

Imagine that we took a large image and divided it into 28x28 pixels squares. Then we can feed each square of a fully connected network that recognizes the handwriting we studied before. If the output “7” is triggered in at least one of the squares, this will be a sign that there is a seven in the whole image. This is exactly what convolutional networks do.

How convolutional networks worked in AlexNet

In convolutional networks, such “stencils” are known as feature detectors, and the area they study is known as the receptive field. Real feature detectors work with much smaller fields than a square with a side of 28 pixels. In AlexNet, feature detectors in the first convolutional layer worked with a receptive field of 11x11 pixels in size. In the subsequent layers, the receptive fields were 3-5 units wide.

During the traversal, the detector of signs of the input image produces a map of signs: a two-dimensional lattice, on which it is noted how strongly the detector was activated in different parts of the image. Convolutional layers usually have more than one detector, and each of them scans the image in search of different patterns. AlexNet had 96 feature detectors on the first layer, giving out 96 feature cards.



To better understand this, consider a visual representation of the patterns studied by each of the 96 AlexNet first layer detectors after training the network. There are detectors looking for horizontal or vertical lines, transitions from light to dark, chess patterns and many other forms.

A color image is usually represented as a pixel map with three numbers for each pixel: the value of red, green, and blue. The first layer of AlexNet takes this view and turns it into a view using 96 numbers. Each “pixel” in this image has 96 values, one for each feature detector.

In this example, the first of 96 values ​​indicates whether any point in the image matches this pattern:



The second value indicates whether some image point coincides with such a pattern:



The third value indicates whether some image point coincides with such a pattern:



And so on for 93 feature detectors in the first AlexNet layer. The first layer gives a new representation of the image, where each pixel is a vector in 96 dimensions (I will explain later that this representation is reduced by 4 times).

This is the first layer of AlexNet. Then there are four more convolutional layers, each of which receives the output of the previous one as an input.

As we saw, the first layer reveals basic patterns, such as horizontal and vertical lines, transitions from light to dark and curves. The second level uses them as a building block for recognizing slightly more complex forms. For example, the second layer could have a feature detector that finds circles with a combination of the outputs of the feature detectors of the first layer that find curves. The third layer finds even more complex shapes by combining features from the second layer. The fourth and fifth find even more complex patterns.

Researchers Matthew Zeiler and Rob Fergus published an excellent work in 2014 , which provides very useful ways to visualize patterns recognized by a five-layer neural network similar to ImageNet.

In the next slideshow taken from their work, each picture, except the first, has two halves. On the right you will see examples of thumbnails that have strongly activated a particular feature detector. They are collected in nine - and each group corresponds to its detector. On the left is a map showing which pixels in this thumbnail are most responsible for the match. This is especially evident on the fifth layer, since there are feature detectors that respond strongly to dogs, logos, wheels, and so on.


The first layer — simple patterns and shapes. The


second layer — small structures begin to appear. Feature


detectors on the third layer can recognize more complex shapes, such as car wheels, honeycombs, and even people’s silhouettes


The fourth layer is able to distinguish complex forms, such as the faces of dogs or the feet of birds.


The fifth layer can recognize very complex forms.

By looking at the images, you can see how each subsequent layer is able to recognize increasingly complex patterns. The first layer recognizes simple patterns that are not like anything. The second recognizes textures and simple shapes. By the third layer, recognizable forms such as wheels and red-orange spheres (tomatoes, ladybugs, something else) become visible.

In the first layer, the side of the receptive field is 11, and in the later ones, from three to five. But remember, later layers recognize feature maps generated by earlier layers, so each of their “pixels” denotes several pixels of the original image. Therefore, the receptive field of each layer includes a larger part of the first image than the previous layers. This is part of the reason that thumbnails in later layers look more complex than in earlier ones.

The fifth, last layer of the network is able to recognize an impressively large range of elements. For example, look at this image that I selected from the upper right corner of the image corresponding to the fifth layer:



The nine pictures on the right may not be alike. But if you look at the nine heatmaps on the left, you will see that this feature detector does not concentrate on objects in the foreground of the photos. Instead, he concentrates on the grass in the background of each of them!

Obviously, a grass detector is useful if one of the categories you are trying to identify is “grass,” but it can be useful for many other categories. After five convolutional layers, AlexNet has three layers connected completely, like our network for handwriting recognition. These layers examine each of the feature maps generated by five convolutional layers, trying to classify the image in one of the 1000 possible categories.

So if there is grass in the background, then with a high probability there will be a wild animal in the image. On the other hand, if there is grass in the background, it is less likely to be an image of furniture in the house. These and other fifth layer feature detectors provide a ton of information about the likely content of the photo. The last layers of the network synthesize this information to provide a fact-supported guess about what is generally depicted in the picture.

What makes convolutional layers different: common input weights

We saw that feature detectors on convolutional layers exhibit impressive pattern recognition, but so far I have not explained how convolutional networks actually work.

The convolutional layer (SS) consists of neurons. They, like any neurons, take a weighted average at the input and use the activation function. Parameters are trained using back propagation techniques.

But, unlike previous NS, the SS is not fully connected. Each neuron receives input from a small fraction of the neurons from the previous layer. And, importantly, convolutional network neurons have common input weights.

Let's look at the first neuron of the first AlexNet SS in more detail. The receptive field of this layer has a size of 11x11 pixels, so the first neuron studies a square of 11x11 pixels in one corner of the image. This neuron receives input from this 121 pixels, and each pixel has three values ​​- red, green and blue. Therefore, in general, the neuron has 363 input parameters. Like any neuron, this one takes a weighted average of 363 parameters, and applies an activation function to them. And, since the input parameters are 363, the weight parameters also need 363.

The second neuron of the first layer is similar to the first. He also studies the squares of 11x11 pixels, but his receptive field is shifted by four pixels relative to the first. The two fields have an overlap of 7 pixels, so the network does not lose sight of interesting patterns that fall on the junction of two squares. The second neuron also takes 363 parameters describing the 11x11 square, multiplies each of them by weight, adds and applies the activation function.

But instead of using a separate set of 363 weights, the second neuron uses the same weights as the first. The top left pixel of the first neuron uses the same weights as the top left pixel of the second. Therefore, both neurons are looking for the same pattern; their receptive fields are simply shifted 4 pixels relative to each other.

Naturally, there are more than two neurons: in the 55x55 lattice there are 3025 neurons. Each of them uses the same set of 363 weights as the first two. Together, all neurons form a feature detector that "scans" the picture for the desired pattern, which can be located anywhere.

Remember that the first AlexNet layer has 96 feature detectors. The 3025 neurons I just mentioned make up one of these 96 detectors. Each of the remaining 95 is a separate group of 3025 neurons. Each group of 3025 neurons uses a common set of 363 weights - however, for each of the 95 groups it has its own.

HFs are trained using the same backpropagation that is used for fully connected networks, but the convolutional structure makes the learning process more efficient and effective.

“Using convolutions really helps - the parameters can be reused,” said Sean Gerrish, an expert in Moscow Region and author. This drastically reduces the number of input weights that the network has to learn, which allows it to produce better results with fewer training examples.

Learning on one part of the image results in improved recognition of the same pattern in other parts of the image. This allows the network to achieve high performance with far fewer training examples.

People quickly realized the power of deep convolutional networks.

AlexNet's work became a sensation in the academic community of Moscow Region, but its importance was quickly understood in the IT industry. Google was especially interested in her.

In 2013, Google acquired a startup founded by the authors of AlexNet. The company used this technology to add a new photo search feature to Google Photos. “We took the advanced research and put it into operation a little more than six months later,” wrote Chuck Rosenberg of Google.

Meanwhile, in the 2013 it has been described how Google uses GSS to recognize addresses with photos of Google Street View service. “Our system helped us extract nearly 100 million physical addresses from these images,” the authors wrote.

Researchers found that the effectiveness of NS grows with increasing depth. “We found that the effectiveness of this approach increases with the depth of the SNA, and the deepest of the architectures we trained show the best results,” wrote the Google Street View team. “Our experiments suggest that deeper architectures can produce greater accuracy, but with a slowdown in efficiency.”

So after AlexNet, the networks began to get deeper. The Google team made a bid at the competition in 2014 - just two years after AlexNet won in 2012. It was also based on a deep SNA, but Goolge used a much deeper network of 22 layers to achieve an error rate of 6.7% - this was a major improvement compared to AlexNet's 16%.

But at the same time, deeper networks worked better only with larger sets of training data. Therefore, Gerrish says that the ImageNet dataset and competition played a major role in the success of the SNA. Recall that at the ImageNet competition, participants are given one million images and are asked to sort them into 1,000 categories.

“If you have a million images for training, then each class includes 1,000 images,” Gerrish said. Without such a large dataset, he said, "you would have too many options for training the network."

In recent years, experts are increasingly focusing on collecting a huge amount of data for training deeper and more accurate networks. That is why companies developing robomobiles concentrate on running on public roads - images and videos of these trips are sent to headquarters and used to train corporate NS.

Computing Deep Learning Boom

The discovery of the fact that deeper networks and larger data sets can improve NS performance has created an insatiable thirst for ever greater computing power. One of the main components of AlexNet's success was the idea that matrix training is used in NS training, which can be efficiently performed on well-parallelizable GPUs.

“The NSs are well parallelized,” said Jai Ten, an MO researcher. Graphics cards - providing tremendous parallel processing power for video games - have proven useful for NS.

“The central part of the work of the GPU, the very fast matrix multiplication, turned out to be the central part of the work of the National Assembly,” Ten said.

All this has been successful for leading manufacturers of GPU, Nvidia and AMD. Both companies have developed new chips specifically tailored to the needs of the MO application, and now AI applications are responsible for a significant part of the GPU sales of these companies.

In 2016, Google announced the creation of a special chip, the Tensor Processing Unit (TPU), designed to operate on the National Assembly. “Although Google was considering the possibility of creating special purpose integrated circuits (ASICs) back in 2006, this situation became urgent in 2013,” a company representative wrote last year. “It was then that we realized that the fast-growing demands of the NS for computing power may require us to double the number of data centers we have.”

At first, only Google’s own services had access to TPUs, but later the company allowed everyone to use this technology through a cloud computing platform.

Of course, Google is not the only company working on AI chips. Just a few examples: in the latest versions of the iPhone chips there is a “neural core” optimized for operations with the NS. Intel is developing its own line of chips optimized for GO. Tesla recently announced the rejection of chips from Nvidia in favor of its own NS chips. Amazon is also rumored to be working on its AI chips.

Why deep neural networks are hard to understand

I explained how neural networks work, but I did not explain why they work so well. It is not clear how exactly the immense number of matrix calculations allows a computer system to distinguish a jaguar from a cheetah, and elderberry from currant.

Perhaps the most remarkable quality of the National Assembly is that they do not. Convolution allows the NS to understand hyphenation - they can tell whether the image from the upper right corner of the image is similar to the image in the upper left corner of another image.

But at the same time, the SNA has no idea about geometry. They cannot recognize the similarity of the two pictures if they are rotated 45 degrees or doubled. SNA do not try to understand the three-dimensional structure of objects, and can not take into account different lighting conditions.

But at the same time, NSs can recognize photos of dogs taken both from the front and from the side, and it does not matter whether the dog occupies a small part of the image, or a large one. How do they do it? It turns out that if there is enough data, a statistical approach with direct enumeration can cope with the task. SNA is not designed so that it can “imagine” how a particular image would look from a different angle or in different conditions, but with a sufficient number of labeled examples, it can learn all the possible variations of the image by simple repetition.

There is evidence that the human visual system works in a similar way. Look at a couple of pictures - first carefully study the first, and then open the second.


First photo



The creator of the image took someone's photograph and turned his eyes and mouth upside down. The picture seems relatively normal when you look at it upside down, because the human visual system is used to seeing eyes and mouths in this position. But if you look at the picture in the correct orientation, you can immediately see that the face is strangely distorted.

This suggests that the human visual system is based on the same crude pattern recognition techniques as NS. If we look at something that is almost always visible in one orientation - the eyes of a person - we can recognize it much better in its normal orientation.

NSs well recognize images using all the context available on them. For example, cars usually drive on roads. Dresses are usually worn on a woman’s body or hang in a closet. Aircraft are usually shot against the sky or they rule on the runway. No one specifically teaches the NS these correlations, but with a sufficient number of labeled examples, the network itself can learn them.

In 2015, researchers from Google tried to better understand the NS, "running them backwards." Instead of using pictures for training NS, they used trained NS to change pictures. For example, they started with an image containing random noise, and then gradually changed it so that it strongly activated one of the output neurons of the NS - in fact, they asked the NS to “draw” one of the categories that it was taught to recognize. In one interesting case, they forced the NS to generate pictures that activate the NS, trained to recognize dumbbells.



“Of course, there are dumbbells here, but not a single image of dumbbells seems complete without the presence of a muscular muscular body lifting them,” Google researchers wrote.

At first glance it looks strange, but in reality it is not so different from what people do. If we see a small or blurry object in the picture, we look for a clue in its surroundings to understand what can happen there. People, obviously, talk about pictures differently, using a complex conceptual understanding of the world around them. But in the end, the STS recognizes images well, because they take full advantage of the whole context depicted on them, and this is not much different from how people do it.