An unexpected look at speed-independent asynchronous circuits
In asynchronous science, the central place is occupied by the property of circuits, called speed independence, in English speed independent (hereinafter SI). It is believed that this property is an analog of the independence of asynchronous circuits from delays of logic elements. Not surprisingly, the term SI is mentioned in almost every work on asynchrony. But periodically some vague doubts arise regarding this term. It is no coincidence that this term is increasingly being replaced by another term called self-synchronization. An appeal to the source will help clarify this situation. We are talking about the second volume of the book of R. Miller's Theory of Switching Circuits, or more precisely, Chapter 10, called Theory of Switching Circuits, Independent of Speed.
So, here is the definition of speed-independent circuits.

A class (equivalences) is a complete set of admissible states of a circuit such that for any state from this set there exists a sequence of admissible states starting from a given state and containing all the states of a given set. In other words, from any state of a class you can get into any state of the same class.
A class (equivalence) is final if it is impossible to pass from the states of a given class to a state belonging to another class.
For example, all living patterns (behaviors) are independent of speed. Also, they do not depend on the speed of the circuit, which eventually necessarily stops, and in a single state.
Further, the author establishes a connection between SI schemes on the one hand, and with semi-modular, sequential, distribution schemes on the other. And in conclusion, he cites a list of remarkable properties of circuits that are independent of speed. The first point is especially interesting. It just says that speed-independent circuits do not depend on delays of logic elements. Unfortunately, the text does not explicitly state the grounds for this conclusion. Perhaps this is the reason for subsequent misunderstandings about the term SI. In reality, this conclusion is completely true. At the beginning of chapter 10, the author provides rules for calculating subsequent states.


The transition of the circuit to the next state is the result of switching the output of some logic element (or the outputs of several elements). That is, the time interval between the creation of conditions for switching a logic element (excitation) and its switching itself is not limited by anything. And such a period of time is a delay of the logical element. That is, from the very beginning, the author proceeds from the assumption that the delays of logic elements can be arbitrarily large. Indeed, the following is written a little further. Well, to dispel all doubts, a quote from the first page of chapter 10.


Thus, an indisputable fact was established: independence from delays of logic elements is not a property of a circuit, but a property of the model in which this circuit is investigated. That is, any circuit, SI or not SI, investigated in the same way as described by R. Miller, is independent of the delays of the logic elements. At the same time, any circuit can be investigated in a model with a limited delay. In such a model, the set of admissible states is a subset of the set of admissible states when considering the same scheme in a model with unlimited element delay. When examining a circuit in a model with a limited element delay, the circuit may be speed independent and at the same time depend on the element delays.
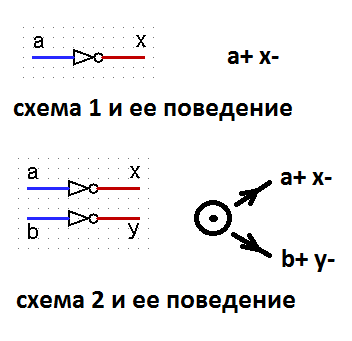
Thus, it turns out that the independence of the circuit from the delays of logic elements is in no way connected with the SI property. Then the question arises: what is the point of introducing a definition of independence from speed? Indeed, consider two patterns and their behavior. Signals a, b for both circuits are input, signals x, y are output. Both schemes implement perfectly reasonable behaviors. But at the same time, circuit 1 does not depend on speed, and circuit 2 does not have such a property. Yes, we can say that the definition of SI was introduced without dividing the signals into input and output. But such a separation of signals by the author was implied, and there is a remark in the text about this.
The meaningfulness and reasonableness of the introduction of the definition of the SI property is revealed only in connection with the semi-modularity property. For circuits with the property of semi-modularity, each signal can remove its excitation only through its switching. Non-semi-modular schemes during physical implementation are fraught with glitches and metastable states. Only semi-modular schemes can be considered stable.
But the connection between the properties of semi-modularity and independence from speed is one-sided. That is, semi-modular schemes are independent of speed, but the converse is not true. SI circuits may not be semi-modular. That is, a really important property dividing circuits according to stability is semi-modularity. It is important to understand that semi-modular circuits can also depend on delays of logic elements, if we consider them in a model with a limited delay.
But that is not all. The semi-modularity property is also defined for autonomous circuits, that is, without dividing the signals into input and output. Because of this, free-choice schemes (behaviors) do not meet the criteria for semi-modularity. Meanwhile, these schemes can be as stable as semi-modular. For example, the above scheme 2 is not semi-modular, but in terms of stability, it is in no way inferior to scheme 1, which is semi-modular.
There is a way out of this impasse. The book J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev “Logic Synthesis for Asynchronous Controllers and Interfaces” defines the definition of output persistency (OP) property.

It is the OP property that is the actual property that separates schemes (behaviors) into stable and not stable. It is the OP property that should take the place of the SI property. It should not be forgotten that independence from delays of logic elements is a property of the model in which circuits (behaviors) are studied. And OP circuits may also be dependent on element delays if considered in a limited delay model.
Despite all the previous criticism, there are no complaints against R. Miller. There are no logical errors in his work. The blame for more than half a century of error lies more with readers who misinterpreted the work of R. Miller.
And finally, a pleasant conclusion from the foregoing. The STG Behavioral Model provides an unlimited delay for logic elements. The rules for changing markings, extracting the truth table are formulated from the assumption of unlimited delay elements. Therefore, any circuit obtained by computing logical functions using STG (either using a truth table or directly using a graph) is obviously independent of the delays of logical elements. True, it must be understood that further manipulations with the resulting scheme can lead to the loss of this valuable quality.
So, here is the definition of speed-independent circuits.

A class (equivalences) is a complete set of admissible states of a circuit such that for any state from this set there exists a sequence of admissible states starting from a given state and containing all the states of a given set. In other words, from any state of a class you can get into any state of the same class.
A class (equivalence) is final if it is impossible to pass from the states of a given class to a state belonging to another class.
For example, all living patterns (behaviors) are independent of speed. Also, they do not depend on the speed of the circuit, which eventually necessarily stops, and in a single state.
Further, the author establishes a connection between SI schemes on the one hand, and with semi-modular, sequential, distribution schemes on the other. And in conclusion, he cites a list of remarkable properties of circuits that are independent of speed. The first point is especially interesting. It just says that speed-independent circuits do not depend on delays of logic elements. Unfortunately, the text does not explicitly state the grounds for this conclusion. Perhaps this is the reason for subsequent misunderstandings about the term SI. In reality, this conclusion is completely true. At the beginning of chapter 10, the author provides rules for calculating subsequent states.


The transition of the circuit to the next state is the result of switching the output of some logic element (or the outputs of several elements). That is, the time interval between the creation of conditions for switching a logic element (excitation) and its switching itself is not limited by anything. And such a period of time is a delay of the logical element. That is, from the very beginning, the author proceeds from the assumption that the delays of logic elements can be arbitrarily large. Indeed, the following is written a little further. Well, to dispel all doubts, a quote from the first page of chapter 10.


Thus, an indisputable fact was established: independence from delays of logic elements is not a property of a circuit, but a property of the model in which this circuit is investigated. That is, any circuit, SI or not SI, investigated in the same way as described by R. Miller, is independent of the delays of the logic elements. At the same time, any circuit can be investigated in a model with a limited delay. In such a model, the set of admissible states is a subset of the set of admissible states when considering the same scheme in a model with unlimited element delay. When examining a circuit in a model with a limited element delay, the circuit may be speed independent and at the same time depend on the element delays.
Thus, it turns out that the independence of the circuit from the delays of logic elements is in no way connected with the SI property. Then the question arises: what is the point of introducing a definition of independence from speed? Indeed, consider two patterns and their behavior. Signals a, b for both circuits are input, signals x, y are output. Both schemes implement perfectly reasonable behaviors. But at the same time, circuit 1 does not depend on speed, and circuit 2 does not have such a property. Yes, we can say that the definition of SI was introduced without dividing the signals into input and output. But such a separation of signals by the author was implied, and there is a remark in the text about this.

The meaningfulness and reasonableness of the introduction of the definition of the SI property is revealed only in connection with the semi-modularity property. For circuits with the property of semi-modularity, each signal can remove its excitation only through its switching. Non-semi-modular schemes during physical implementation are fraught with glitches and metastable states. Only semi-modular schemes can be considered stable.
But the connection between the properties of semi-modularity and independence from speed is one-sided. That is, semi-modular schemes are independent of speed, but the converse is not true. SI circuits may not be semi-modular. That is, a really important property dividing circuits according to stability is semi-modularity. It is important to understand that semi-modular circuits can also depend on delays of logic elements, if we consider them in a model with a limited delay.
But that is not all. The semi-modularity property is also defined for autonomous circuits, that is, without dividing the signals into input and output. Because of this, free-choice schemes (behaviors) do not meet the criteria for semi-modularity. Meanwhile, these schemes can be as stable as semi-modular. For example, the above scheme 2 is not semi-modular, but in terms of stability, it is in no way inferior to scheme 1, which is semi-modular.
There is a way out of this impasse. The book J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev “Logic Synthesis for Asynchronous Controllers and Interfaces” defines the definition of output persistency (OP) property.

It is the OP property that is the actual property that separates schemes (behaviors) into stable and not stable. It is the OP property that should take the place of the SI property. It should not be forgotten that independence from delays of logic elements is a property of the model in which circuits (behaviors) are studied. And OP circuits may also be dependent on element delays if considered in a limited delay model.
Despite all the previous criticism, there are no complaints against R. Miller. There are no logical errors in his work. The blame for more than half a century of error lies more with readers who misinterpreted the work of R. Miller.
And finally, a pleasant conclusion from the foregoing. The STG Behavioral Model provides an unlimited delay for logic elements. The rules for changing markings, extracting the truth table are formulated from the assumption of unlimited delay elements. Therefore, any circuit obtained by computing logical functions using STG (either using a truth table or directly using a graph) is obviously independent of the delays of logical elements. True, it must be understood that further manipulations with the resulting scheme can lead to the loss of this valuable quality.
