How we halved the cost of an introductory lesson by looking at a solution from airlines

A free introductory lesson is the Skyeng School feature. A potential student can get acquainted with the platform on it, check his level of English, and finally, just have fun. For the school, the introductory lesson is part of the sales funnel, followed by the first payment. It is conducted by an introductory lesson methodologist - a special person who combines a teacher and a salesperson, his time is paid regardless of whether the client bought the first package or not, and whether he appeared at all for the lesson. Absenteeism is a very common occurrence due to which the price of a lesson becomes too high.

In this article, we will describe how, with the help of the analytical model and experience of airlines, we were able to reduce the costs of the introductory lesson by almost half.

The Skyeng sales funnel consists of five steps: registering on the site, calling the first line of sales with an entry to the introductory lesson, an introductory lesson, ringing the second line of sales, paying for the first package. Earlier, after the first call, we set a lesson time for a particular introductory lesson methodologist, who was waiting for the student at that time. If a person signed up and did not come, the methodologist wastes his time, and school - money to pay for this time. Absenteeism occurs on average in half the cases; one third of customers buy the first package after an introductory lesson. Thus, the conversion from recording to an introductory lesson into payment is only 0.15. A successful (converted to payment) introductory lesson in the old scheme cost us 4,000 rubles, and we had to do something about it.

You can simply refuse it, but in this case, the final conversion from lead to payment will drop significantly, which does not suit us. We’ll have to look for another solution, build models, count and experiment.

First pancake

We turned to the experience of airlines, specifically to the practice of overbooking. Carriers know that 100% of passengers who have bought a ticket are rarely on a flight, and take advantage of this by selling more tickets than seats on the plane. If suddenly all the passengers arrive for landing, you can find volunteers among them who are ready to fly off for the next bun on the next flight. Airlines thus increase their profits, and we can reduce costs by a similar method.

So: we refuse the record to a specific person, we create a pool of methodologists of the introductory lesson, we scatter applications between them in the expectation that half will not appear. And if more has come, we suggest you sign up for another day. We launched such an MVP into the test and immediately realized that we had done everything wrong.

Half of those entering the introductory lesson are statistics, in reality, the proportion varies greatly depending on the time, day, channel from which the person came. Moreover, more than 80% of potential students, in response to a proposal to postpone the lesson, either immediately fall off, or do not come by the second record. All this could lead to the fact that on bad days we would lose up to a third of customers. The test was turned off and went to do everything in a smart way.

Model, forecasts, polynomials

First of all, it was necessary to find out what the proportion of those who go to the introductory lesson depends on. The first observation is that it depends on the marketing channel where the person came from. We divide these channels from the point of view of conversion into payment into “hot”, where the conversion is higher, “warm” and “cold”, where it is lower; it turned out that the "channel temperature" affects the conversion to the output of the introductory lesson in much the same way.

Continuing the aviation analogy, we made different “check-in desks” for leads from different channels, placing them with coefficients corresponding to the historical probability of this channel coming out: 0.8, 0.4 and 0.2. For “hot” channels, we allocate more methodologists, “cold” - less. This worked better, but still on bad days there were more than 20% of “departures” (situations where more clients attended the introductory lesson than there were free methodologists). They tried to increase the coefficients by adding a margin of 0.1: on the one hand, the more we get the methodologists out, the less we lose customers, on the other - the costs of conducting introductory lessons are growing.

From these observations, the second MVP grew. For each enrolled, we make a forecast of the probability of his going to an introductory lesson. We make a joint probability distribution and confidence interval with a confidence level of 95%. For rare cases when more clients are coming out than planned, we hold a reserve pool of methodologists - teachers who are currently engaged in non-urgent work such as checking essays.

To calculate the forecast for a particular student, we built a statistical model based on our historical data and taking into account several factors: channel, region, child / adult, private / corporate client, time from recording to the introductory lesson.

The model operates with the following concepts:

• slot : date and time of the introductory lesson;
• correction factor : the probability of an abnormal exit on this day and hour;
• application weight : admissible probability of a given client's exit
• Departure : Unserved application (client exited, all methodologists are busy);
• simple methodologist : it turned out less than predicted, people are sitting idle;
• restriction :% on the confidence interval, after which the model prohibits adding orders to the slot.

Each slot contains N methodologists, and the slot itself has a correction factor k (with a base of 100). The number of methodologists available for the model is defined as round (N * k / 100). When an application appears, the model determines its weight , looks at the sum of such weights already in the slot, and determines the slot as available if, as a result of adding this application, the sum of the application weights in the slot does not exceed the number of methodologists. The metrics for evaluating the model are: the proportion of departures (necessary to minimize), slot loading (maximized), the waiting time for the introductory lesson by the client (minimized). Variable model parameters include application weight and restriction .

To predict how many customers will be released, the formula for the product of probabilities was used:

Considering all possible combinations of outputs, we get a very close to natural probability distribution. The distribution for one hundred customers looks like this:

Applying the confidence interval to it, we can adjust the aggressiveness of the model. For example, shifting the restriction to the left increases it, i.e. we release more clients with the same number of methodologists, and a shift to the right reduces it, because restriction is triggered earlier. Example with restrictions of 90% and 57%: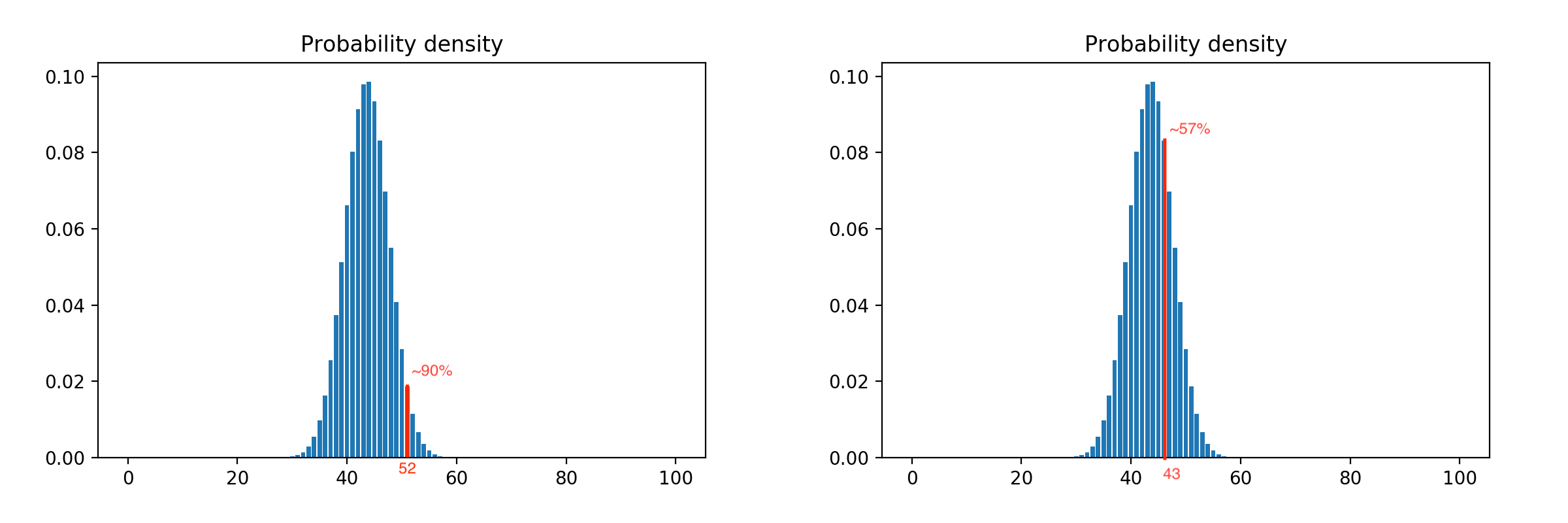

In addition, the aggressiveness of the model can be adjusted by a correction factor: a decrease reduces it, an increase raises it. This is useful when we know that on a particular day / hour, certain external factors can make the abnormality.

The formula with multiplication of probabilities showed itself well in tests, but was difficult from a computational point of view, so we rewrote it with polynomials:

The disadvantages of the model include:

• due to the fact that it is based on historical data, it does not respond well to sudden changes in exit;
• if the methodologist has a force majeure event and he drops out of the slot, this is an almost guaranteed departure, managers need to urgently reassign the lesson;
• if the dynamic marking of the “heat” of the channels falls, the model incorrectly estimates the probability of the client coming out.

As a result of using this model, we received up to 45% cost savings on the introductory lesson with minimal loss to customers.

Why not machine learning?

Because the statistical model works pretty well, and instead of improving the accuracy of an existing forecast using ML, it’s more profitable to direct the efforts of ML developers to other tasks.

For example, we are developing a scoring system for a potential customer, remotely similar to a banking one. Using scoring, banks determine the probability of a loan repayment, and we can determine the probability of a first payment. If it is very low, there is no need to spend resources on organizing an introductory lesson; if, on the contrary, it is very high, you can immediately send the client to the payment page.

But this story is for another time.