I am a robotics researcher and at the same time my hobby is game development. My specialization is the planning of multidimensional movement of robotic arms. Motion planning is a very important topic for game developers, it comes in handy every time you need to move a controlled AI character from one point to another.

In the process of studying game development, I found many tutorials that talked about traffic planning (usually referred to in the literature on game development as “finding the way”), but most of them did not go into the details of what traffic planning is from a theoretical point of view . As far as I can tell, most games rarely use some other movement planning, except for one of three serious algorithms: search on A * grids, visibility graphs and flow fields. In addition to these three principles, there is a whole world of theoretical studies of motion planning, and some of them may be useful to game developers.

In this article, I would like to talk about standard traffic planning techniques in my context and explain their advantages and disadvantages. I also want to introduce basic techniques that are not commonly used in video games. I hope they shed light on how they can be applied in game development.

Movement from point A to point B: agents and goals

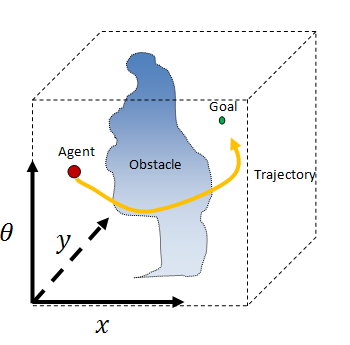
Let's start with the fact that we have an AI-controlled character in the game, for example, an enemy in a shooter or a unit in a strategy game. We will call this character an agent. The agent is located in a specific place in the world called its “configuration”. In two dimensions, the agent configuration can be represented by just two numbers (usually x and y). The agent wants to get to some other place in the world, which we will call the goal (Goal).

Let's imagine the agent as a circle living in a flat two-dimensional world. Suppose an agent can move in any direction it needs. If there is nothing but empty space between the agent and its target, then the agent can simply move in a straight line from its current configuration to the target. When he reaches the goal, he stops. We can call this the “Walk To algorithm.”

Алгоритм: WALK TO

1. Если не цель:
   1. Двигаться к цели.
2. Иначе: Остановиться.

If the world is completely empty, then this fits perfectly. It may seem obvious that we need to move from the initial configuration to the target configuration, but it is worth considering that the agent could move in a completely different way to get from the current configuration to the target. He could cycle around until he reached the goal or move away from it fifty kilometers before returning and stopping on the target.

So why do we find the straight line obvious? Because in a sense, this is the "best" way of moving. If we assume that the agent can only move at a constant speed in any direction, then the straight line is the shortest and fastest way to get from one point to another. In this sense, the Walk To algorithm is optimal.. In this article we will talk a lot about optimality. In fact, when we talk about the optimality of an algorithm, we mean that it is “best of all” with a certain criterion of “best”. If you want to get from point A to point B as quickly as possible and there is nothing on the way, then nothing can compare with a straight line.

And in fact, in many games (I would say, even in most games), the Walk To direct algorithm is ideal for solving a problem. If you have small 2D enemies in corridors or rooms that don’t need to wander through the mazes or follow the player’s orders, then you will never need anything more complicated.

But if something suddenly appeared on the way?


In this case, the object on the path (called an Obstacle) blocks the agent’s path to the target. Since the agent can no longer move directly to the target, he simply stops. What happened here?

Although the Walk To algorithm is optimal , it is not complete . A “complete” algorithm is able to solve all the problems to be solved in its field in a finite time. In our case, an area is circles moving along a plane with obstacles. Obviously, simply moving directly to the goal does not solve all the problems in this area.

To solve all the problems in this area and solve them optimally, we need something more sophisticated.

Reactive Planning: Beetle Algorithm

What would we do if there was an obstacle? When we need to get to the goal (for example, to the door), and there is something on the way (for example, a chair), then we just go around it and continue to move towards the goal. This type of behavior is called "avoiding obstacles." This principle can be used to solve our problem of moving an agent to a target.

One of the simplest obstacle avoidance algorithms is the beetle algorithm . It works as follows:

Алгоритм : BUG

1. Рисуем прямую линию от агента до цели. Назовём её M-линией.
2. Агент делает единичный шаг вдоль M-линии пока не будет соблюдаться одно из следующих условий:
   
   1. Если агент достиг цели, то остановиться.
   2. Если агент касается препятствия, то следовать вдоль препятствия по часовой стрелке, пока мы снова не попадём на M-линию, если при этом мы ближе к цели, чем были изначально до достижения M-линии. Когда мы достигаем M-линии, продолжить с шага 2.

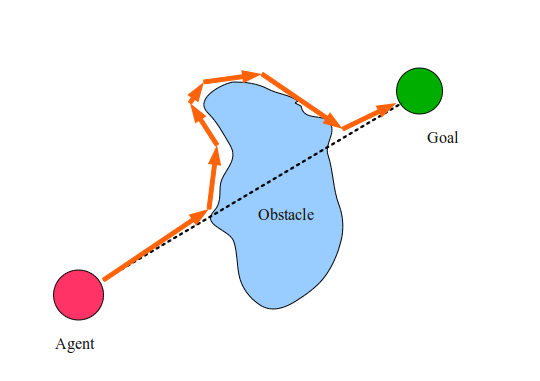
Step 2.2 requires explanation. In fact, the agent remembers all cases of encountering the M-line for the current obstacle, and leaves the obstacle only when it is on the M-line and closer to the target than at any other time before. This is to avoid getting the agent into an infinite loop.

In the figure above, the dashed line shows the M-line, and the orange arrows indicate the steps taken by our agent to achieve the goal. They are called the agent trajectory . Surprisingly, the beetle algorithm very simply solves many problems of this type. Try to draw a bunch of crazy figures and see how well it works! But does the bug algorithm work for every task? And why does it work?

The simple beetle algorithm has a lot of interesting features and demonstrates many key concepts, which we will return to in this article. These concepts are: trajectory, politics, heuristics, completeness and optimality.

We have already mentioned the concept of a trajectory , which is a simple sequence of configurations or movements performed by an agent on its way. The beetle algorithm can be considered a Trajectory Planner, that is, an algorithm that receives the initial configuration and the configuration of the target, and returns the trajectory from the beginning to the target. (In the literature on game development, it is also sometimes called a “path planner”).

But we must also mention the concept of politics. If we do not interpret the beetle algorithm as returning the full trajectory from the beginning to the target, but interpret it as transmitting to the agent a set of instructions that allow you to get to the target from anywhere , simply using your own configuration as a guide, then the beetle algorithm can be called a control policy (Control Policy). A management policy is simply a set of rules that, based on the state of the agent, determines what actions the agent should take next.

In the beetle algorithm, the M-line is a clear indicator of where the agent should be located next. Why did we choose to follow the M-line, and not, say, a line from the current position of the agent to the target? The answer is that the M-line is just a heuristic. Heuristics is a general rule used to report the next step in an algorithm. This rule gives some human knowledge about the algorithm. Choosing a heuristic is often an important part of developing such an algorithm. If you select the wrong heuristic, the algorithm may be completely inoperative.

Believe it or not (I did not believe at first), but the beetle algorithm solves all the problems to be solved in the field of two-dimensional circles moving from the beginning to the goal. This means that regardless of the location of the agent or target, if the agent can achieve the goal, then the beetle algorithm will allow him to do this. Proof of this is beyond the scope of this article, but you can read about it if you wish. If an algorithm can solve all problems in its field for which there are solutions, then it is calledcomplete algorithm .

But despite the fact that the beetle algorithm can solve all problems of this type, the trajectories created by it are not always the best possible categories by which the agent can achieve the goal. In fact, the bug algorithm can sometimes cause the agent to do pretty stupid things (just try to create an obstacle that is small in the clockwise direction and huge in the other direction, and you will understand what I mean. If we define “best” as “occupying the shortest time ”, then the bug algorithm is by no means optimal .

Optimal planning: visibility graph

And if we need to solve the problem of the movement of circles among obstacles along the optimal (shortest) path? To do this, we can use geometry to figure out what the optimal algorithm for solving this problem should be. First, note the following:

• On two-dimensional Euclidean planes, the shortest path between two points is a straight line.
• The length of a sequence of straight paths is the sum of the lengths of each of the lines.
• Since the polygon consists of straight lines (or edges), the shortest path that completely bypasses the convex polygon contains all the edges of the polygon.
• To go around a non-convex polygon, the shortest path contains all the edges of the convex hull of the polygon.
• A point located exactly on the edge of the polygon touches this polygon

Understanding the definitions of “convexity”, “non-convexity” and “convex hull” is not very important for understanding this article, but these definitions are enough to create an optimal trajectory planner. Let's make the following assumptions:

• Our agent is a two-dimensional point of infinitely small size.
• All the obstacles of the world can be reduced to closed polygons .
• Our agent can move in any direction in a straight line.

Then we can find the optimal plan for the agent to achieve the goal, creating what is called the graph of visibility of the world. Besides geometry, we also need to learn a little about graphs. Graph theory is not the topic of this article, but essentially graphs are just groups of abstract objects (called nodes ) connected to other nodes by abstract objects called edges . We can use the power of graphs to describe the world in which the agent lives. We can say that a node is any place where an agent can be located without touching anything. An edge is a path between nodes along which an agent can move.

Given this, we can define a visibility graph planner as follows:

Алгоритм: VISIBILITY GRAPH PLANNER

• Создаём пустой граф с названием G.
• Добавляем агента как вершину графа G.
• Добавляем цель как вершину графа G.
• Помещаем все вершины всех многоугольников мира в список.
• Соединяем все вершины многоугольников в граф G в соответствии с их рёбрами.
• Для каждой вершины V списка:
  
  • Пытаемся соединить V с агентом и целью. Если прямая линия между ними не пересекает ни один из многоугольников, то добавляем эту линию как ребро в граф G.
  • Каждую другую вершины в каждом другом многоугольнике пытаемся соединить прямой линией с V. Если линия не пересекает ни один из многоугольников, то добавляем линию как ребро графа G.
  • Теперь выполняем планировщик графов (например, алгоритм Дейкстры или A*) для графа видимости, чтобы найти кратчайший путь от агента до цели.

The visibility graph is as follows: (dashed lines)


And the final path looks like this:


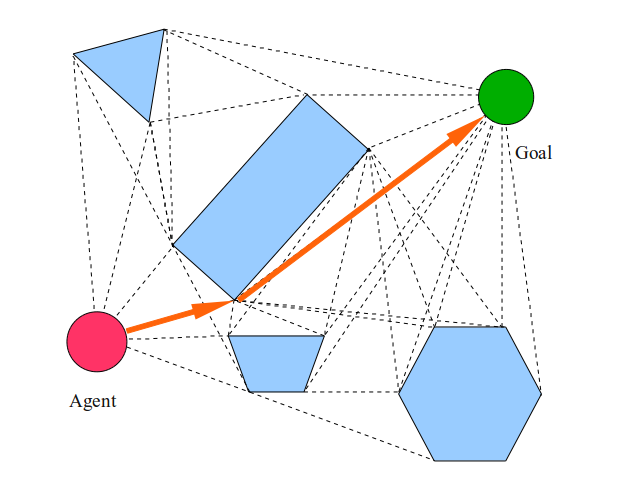
Due to the assumptions that the agent is an infinitesimal point that can move in straight lines from any one location to any other, we have a trajectory that passes exactly through corners, faces and free space, clearly minimizing the distance that the agent must travel to goals.

But what if our agent is not a point? Notice how the orange path leads the agent between the trapezoid and the rectangle. Obviously, the agent cannot squeeze through this space, so we need to solve this problem somehow differently.

One solution is to assume that the agent is not a point, but a disk. In this case, we can simply inflate all the obstacles to the radius of the agent, and then plan as if the agent is a point in this new bloated world.


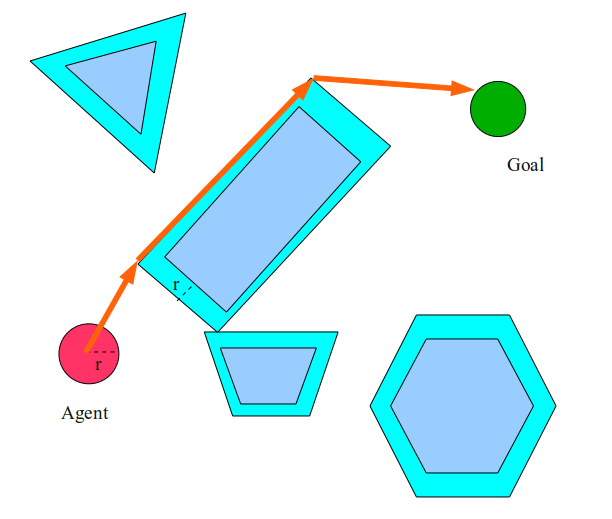
In this case, the agent will choose the path to the left, and not to the right of the rectangle, because it simply does not fit in the space between the trapezoid and the rectangle. This “bloat” operation is actually incredibly important. In essence, we have changed the world so that our assumption that the agent is a point remains true.

This operation is called configuration space calculation .of the world. Configuration space (or C-Space) is a coordinate system in which the configuration of our agent is represented by a single point. An obstacle in the workspace is converted into an obstacle in the configuration space by placing the agent in a conditional configuration and checking for collisions of the agent. If in this configuration the agent touches an obstacle in the working space, then it becomes an obstacle in the configuration space. If we have a non-circular agent, then for inflating obstacles we use the so-called Minkowski sum
.

In the case of two-dimensional space, this may seem boring, but this is precisely what we are doing to “inflate” obstacles. The new "bloated" space is actually a configuration space. In more multidimensional spaces, things get more complicated!

The visibility graph planner is a great thing. It is both optimal and complete , and it does not rely on any heuristic . Another great advantage of the visibility graph planner is its moderate multi-query capability . A multi-query scheduler is able to reuseold calculations when working with new goals. In the case of the visibility graph, when changing the location of the target or agent, we only need to rebuild the edges of the graph from the agent and from the target. These advantages make such a scheduler extremely attractive to game programmers.

In fact, many modern games use visibility graphs for planning. A popular variation on the visibility graph principle is the Nav (igation) Mesh . In Nav Mesh, sometimes graphs of visibility are used as a basis (together with other heuristics for distance to enemies, objects, etc.). Nav Mesh is subject to change by designers or programmers. Each Nav Mesh is stored as a file and used for each individual level.

Here is a screenshot of the Nav Mesh used in the video gameOverlord :


Despite all its advantages, visibility graph methods have significant drawbacks. For example, calculating a visibility graph can be a rather expensive operation. As the number of obstacles increases, the size of the visibility graph grows significantly. The cost of computing the visibility graph grows as a square of the number of vertices. In addition, if you change any obstacles to maintain optimality, you will likely need a full recalculation of the visibility graph.

Game programmers invented all sorts of tricks to speed up the creation of graphs using heuristics to select nodes to which you need to try to join through the edges. Also, game designers can give the graph visibility algorithm hints so that it determines which nodes to connect in the first place. All these tricks lead to the fact that the graph of visibility ceases to be optimal and sometimes requires the monotonous work of programmers.

However, the most serious problem with visibility graphs (in my opinion) is that they are poorly generalized. They solve one problem (planning on a 2D plane with polygon obstacles), and they solve it incredibly well. But what if we are not on a two-dimensional plane? What if our agent cannot be represented in a circle? What if we do not know what the obstacles will be, or they cannot be represented in the form of polygons? Then we cannot use visibility graphs to solve our problem without tricks.

Fortunately, there are other methods closer to the “run and forget” principle that solve some of these problems.

Search by grate: A * and its variations

Visibility graphs work because they use optimizing search qualities for abstract graphs, as well as the fundamental rules of Euclidean geometry . Euclidean geometry gives us a “fundamentally correct” graph to search for. And the abstract search itself is engaged in optimization.

But what if we completely abandon Euclidean geometry and simply solve the whole problem by searching through abstract graphs? Thus, we can eliminate the mediator in the face of geometry and solve many different types of problems.

The problem is that we can use many different approaches to transfer our task to the graph search area. What will be the nodes? What exactly are ribs? What does connecting one node to another mean? The performance of our algorithm depends to a large extent on how we answer these questions.

Even if the graph search algorithm gives us an “optimal” answer, it is “optimal” in terms of only its own internal structure. This does not imply that the “optimal” answer according to the graph search algorithm is the answer we need.

Given this, let's define a graph in the most common way: as a grid . Here's how it works:

Алгоритм: DISCRETIZE SPACE

• Допустим, что конфигурационное пространство имеет постоянный размер во всех измерениях.
• Дискретизируем каждое изменение так, чтобы в нём было постоянное количество ячеек.
• Каждую ячейку, центр которой находится в конфигурационном пространстве внутри препятствия, пометим как непроходимую.
• Аналогично, каждую ячейку, центр которой не находится в препятствии, пометим как проходимую.
• Теперь каждая проходимая ячейка становится узлом.
• Каждый узел соединяется со всеми смежными проходимыми соседями в графе.

“Adjacent” is another aspect to be careful with. Most often, it is defined as “ any cell that has at least one common angle with the current cell ” (this is called the “Euclidean adjacency”) or “ any cell that has at least one common face with the current cell ” (this is called the “Manhattan adjacency” ) The answer returned by the graph search algorithm depends very much on the choice of adjacency definition.

Here's what the sampling phase will look like in our case study:


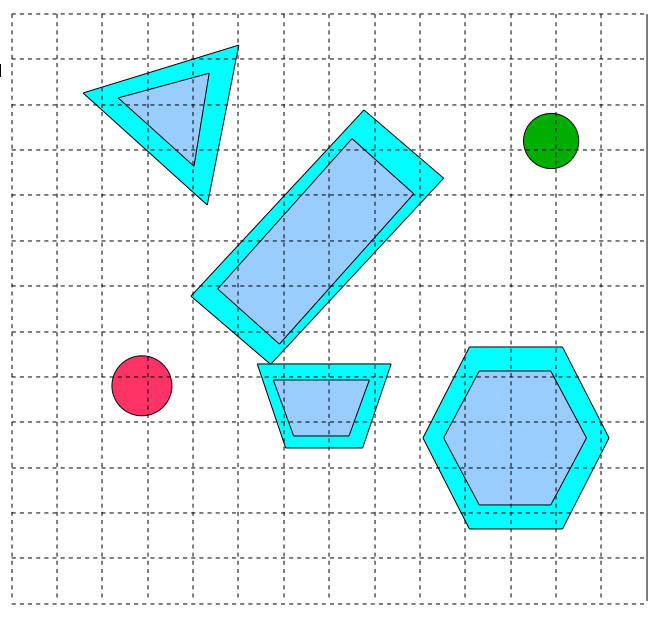
If we search in this graph according to the Euclidean adjacency metric, we will get something like this:


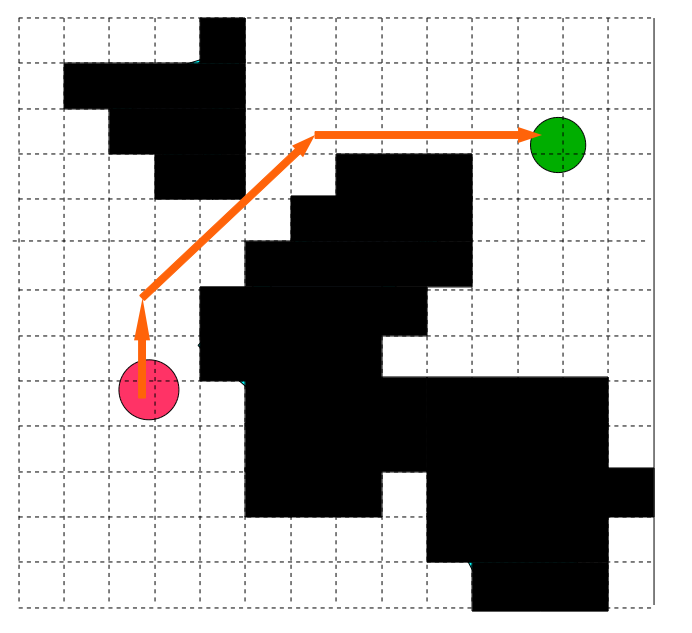
There are many other graph search algorithms that can be used to solve the lattice search problem, but the most popular is A * . A * is akin to Dijkstra's algorithm , which performs a search on nodes using heuristics, starting from the starting node. A * is well researched in many other articles and tutorials, so I will not explain it here.

A * and other grid graph search methods are some of the most common scheduling algorithms in games, and a discretized grid is one of the most popular ways to structure A *. For many games, this search method is ideal because many games still use tiles or voxels to represent the world.

Search methods for graphs on a discrete lattice (including A *) are optimal according to their internal structure . They are also full resolution . This is a weaker form of completeness, which says that when the fineness of the lattice tends to infinity (i.e., when the cells tend to infinitely small size), the algorithm solves more and more problems to be solved.

In our specific example, the grid search method is single-query , not multi-query, because a graph search usually cannot reuse old information when generalizing to new target and start configurations. However, the sampling step, of course, can be reused.

Another key advantage (in my opinion, the main one) of graph-based methods is that they are completely abstract. This means that additional costs (such as ensuring safety, smoothness, proximity of the necessary objects, etc.) can be taken into account and automated automatically. In addition, to solve completely different problems, you can use the same abstract code. In the DwarfCorp game , we use the same A * scheduler for both motion planning and symbolic action planning (used to represent the actions that agents can take as an abstract graph).

However, grating searches have at least one serious flaw: they are incredibly memory intensive. If every node is built in a naive way from the beginning, then with an increase in the size of the world, your memory will very quickly run out. Most of the problem is that the grid has to store large amounts of empty space. To minimize this problem, optimization techniques exist, but fundamentally, as the size of the world and the number of dimensions of the problem increase, the amount of memory in the lattice increases tremendously. Therefore, this method is not applicable for many more complex tasks.

Another serious drawback of the method is that searching by graphs in itself can take quite a bit more time. If several thousand agents move at the same time in the world or many obstacles change their position, then a lattice search may not be applicable. In our game DwarfCorp, planning has been devoted to several threads. It eats up a bunch of processor time. In your case, this can also be!

Management Policies: Potential Functions and Flow Fields

Another way to solve the problem of traffic planning is to stop thinking about it in the categories of planning trajectories and begin to perceive it in the categories of management policies . Remember, we said that the beetle algorithm can be perceived both as a trajectory planner and as a management policy? In that section, we defined a policy as a set of rules that receives a configuration and returns an action (or “control input”).

The beetle algorithm can be thought of as a simple management policy that simply tells the agent to move toward the target until he comes across an obstacle, and then bypass the obstacle clockwise. An agent can literally follow these rules, moving along its path to the goal.

The key advantages of management policies are that they generally do not rely on an agent who has something more than local knowledge of the world, and that they are incredibly fast in computing. Thousands (or millions) of agents can easily follow the same management policy.

Can we come up with any management policies that work better than the bug algorithm? It is worth considering one of them, a very useful " potential field policy ". She performs the simulation of an agent in the form of a charged particle attracted to the target and repelled by obstacles:

Алгоритм: POTENTIAL FIELD POLICY

• Определяем вещественные константы a и b
• Находим вектор в конфигурационном пространстве от агента до цели и обозначаем его как g.
• Находим ближайшую точку препятствия в конфигурационном пространстве и обозначаем его как o.
• Находим вектор от o до агента и обозначаем его как r.
• Входной сигнал управления имеет вид u = a * g^ + B * r^, где v^ обозначает нормализованный вектор v.
• Перемещаем агента согласно входному сигналу управления.

Understanding this policy requires some knowledge of linear algebra . In essence, the input control signal is a weighted sum of two terms: a member of attraction and a member of repulsion . The choice of weights in each member significantly affects the final trajectory of the agent.


Using the potential field policy, you can make agents move in an incredibly realistic and smooth way. You can also easily add additional conditions (proximity to the desired object or distance to the enemy).

Since the potential field policy is calculated extremely quickly in parallel computing, this way you can very effectively control thousands and thousands of agents. Sometimes this management policy is pre-computed and stored in the grid for each level, after which it can be changed by the designer in the way he needs (then it is usually called the flow field ).

In some games (especially in strategic ones) this method is used with great efficiency. Here is an example of the flow fields used in the strategy game Supreme Commander 2so that the units naturally avoid each other, preserving the construction:


Of course, the functions of the flow fields and potential fields have serious drawbacks. Firstly, they are by no means optimal . Agents will be distributed by the flow field, regardless of how long it takes to reach the target. Secondly (and, in my opinion, this is most important), they are by no means complete . What if the control input is reset before the agent reaches the target? In this case, we say that the agent has reached a " local minimum ." You might think that such cases are quite rare, but in fact they are quite easy to construct. Simply place a large U-shaped obstacle in front of the agent.

Finally, flow fields and other management policies are very difficult to configure. How do we pick the weights of each member? In the end, they require manual tuning to get good results.

Typically, designers have to manually adjust flow fields to avoid local minima. Such problems limit the possible utility in the general case of flow fields. However, in many cases they are useful.

Configuration space and the curse of dimension

So, we discussed the three most popular motion planning algorithms in video games: grids, visibility graphs, and flow fields. These algorithms are extremely useful, easy to implement, and fairly well understood. They work ideally in the case of two-dimensional problems with round agents moving in all directions of the plane. Fortunately, almost all tasks in video games belong to this case, and the rest can be imitated by cunning tricks and hard work of the designer. It is not surprising that they are so actively used in the gaming industry.

But what have the researchers of traffic planning been doing in the last few decades? To everyone else. What if your agent is not a circle? What if it is not on a plane? What if he can move in any direction? What if goals or obstacles are constantly changing? Answering these questions is not so simple.

Let's start with a very simple case, which seems to be quite simple to solve using the methods we have already described, but which really cannot be solved by these methods without fundamentally changing them.

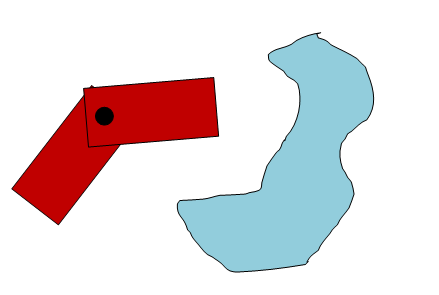
What if the agent is not a circle but a rectangle? What if agent rotation is important ? Here is what the picture I am describing looks like:


In the case shown above, the agent (red) is like a shopping cart that can move in any direction. We want to move the agent so that it is exactly on top of the target and is turned in the right direction.

Here we can presumably use the bug algorithm, but we will need to carefully handle the turns of the agent so that he does not encounter obstacles. We will quickly become entangled in the chaos of rules, which will not be as elegant as in the case of a round agent.

But what if you try to use the visibility graph? For this, the agent must be a point. Remember how we did the trick and inflated the objects for the round agent? Perhaps in this case it will be possible to do something similar. But how much do we need to inflate objects?

A simple solution would be to select the “worst case scenario” and calculate the planning with this calculation. In this case, we simply take the agent, determine the circle that describes it, and take the agent to an equal circle of this size. Then we inflate the obstacles to the desired size.


It will work, but we will have to sacrifice the fullness. There will be many tasks that we can not solve. Take for example a task in which a long and thin agent must get through a “keyhole” to achieve its goal:


In this scenario, the agent can reach the target by entering the well, turning 90 degrees, then reaching the next well, turning 90 degrees and leaving it. With a conservative approximation of the agent through the describing circle, this problem will be impossible to solve.

The problem is that we did not properly account for the agent configuration space. Up to this point, we have only discussed 2D planning, surrounded by 2D obstacles. In such cases, the configuration space is well transformed from two-dimensional obstacles to another two-dimensional plane, and we observe the effect of "inflating" obstacles.

But in fact, the following happens here: we have added another dimension to our planning task. The agent has not only a position in x and y, but also a turn. Our task is actually the task of three-dimensional planning. Conversions between workspaces and configuration spaces are now becoming much more complex.

You can take it this way: imagine that the agent has completed a certain turn (which we will designate "theta"). Now we move the agent to each point of the workspace with a given rotation, and if the agent touches an obstacle, then we consider this point to be a collision in the configuration space. Such operations for obstacles-polygons can also be implemented using Minkowski sums .


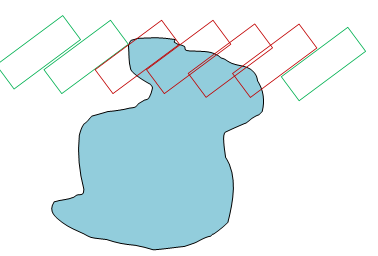
In the diagram above, we have one agent passing through an obstacle. The red contours of the agent show the configurations that are in collision, and the green contours show the configurations without collisions. This naturally leads to another “inflating” of the obstacles. If we execute it for all possible positions (x, y) of the agent, we will create a two-dimensional slice of the configuration space.

Now we just increase the theta by a certain amount and repeat the operation, getting another two-dimensional slice.


Now we can superimpose the slices one on top of the other, aligning their x and y coordinates, as if folding sheets of graph paper:


If we cut the aunt infinitely thinly, then as a result we get a three-dimensional configuration space of the agent. This is a continuous cube, and the theta rotates around it from the bottom up. Obstacles turn into strange cylindrical figures. The agent and his goals become just points in this new strange space.


It's pretty hard to put in your head, but in a sense, this approach is beautiful and elegant. If we can imagine obstacles in two dimensions, where each dimension is simply the position of the agent in x and y coordinates, then we can also imagine obstacles in three dimensions, where the third dimension is the rotation of the agent.

What if we wanted to add another degree of freedom to the agent? Suppose we would like to increase or decrease its length? Or would he have arms and legs that also need to be considered? In such cases, we do the same - just add measurements to the configuration space. At this stage, it becomes completely impossible to visualize, and in order to understand them, one has to use concepts such as “hyperplane”, “manifold with constraints” and “hyper ball”.


An example of a four-dimensional planning problem. The agent consists of two segments with an axis connecting them.

Now that our agent is just a point in 3D space, we can use conventional algorithms to find a solution to any movement planning problem. If we wanted to, we could create a grid of voxels in a new 3D space and use A *. If you thought, you could also find a representation of the configuration space as a polygonal mesh, and then use the visibility graph in 3D.

Similarly, for other dimensions, we can do the following:

1. Calculate the configuration space of the agent and obstacles.
2. Run A * or Nav Mesh in this space.

Unfortunately, these operations have two huge problems:

1. Вычисление N-мерного конфигурационного пространства является NP-сложной задачей.
2. Оптимальное планирование в N-мерном конфигурационном пространстве является NP-сложным.

The technical term from computer science, “ NP-complex ”, means that the task when it increases becomes exponentially more difficult, bringing with it many other theoretical difficulties.

In practice, this means that if we begin to add measurements to planning tasks, then very soon we will run out of computing power or memory, or both. This problem is known as the curse of dimension . In three dimensions, we can get by with A *, but as soon as we get to 4, 5 or 6 dimensions, A * quickly becomes useless (despite recent studies by Maxim Likhachev , which made it possible to ensure its good enough work).

The simplest example of a six-dimensional planning task is called the piano moving task.". Its wording: how to move a solid-state object (for example, a piano) from point A to point B in 3D space, if it can be moved and rotated in any direction?


An example of the task of moving a piano from OMPL

Surprisingly, despite its simplicity, this task has remained unresolved for decades.

For this reason, games basically adhere to simple two-dimensional problems and simulate everything else (even when having a solution to something like the task of moving the piano seems to be a fundamental part of the AI ​​of a three-dimensional game).

Unsolved problems

In the 70s and 80s, motion planning studies focused on fast ways to calculate configuration space and good compression heuristics to reduce the dimension of some planning tasks. Unfortunately, these studies did not lead to the creation of simple general solutions to problems in a large number of dimensions. The situation did not change until the 90s and the beginning of the zero, when robotics researchers did not begin to move the progress of solving common multidimensional problems.

Today, planning in multidimensional spaces is much better studied. All this happened thanks to two main discoveries: randomized schedulers and fast track optimizers . I will talk about them in the following sections.

The difference between finding a route and planning for traffic

I noticed that after publishing a draft of this article, some readers were confused by my terminology. In the literature on game development, the action of moving from point A to point B is usually called " finding a path ", and I called it " planning a move ." In essence, motion planning is a generalization of a path search with a looser definition of a “point” and a “path” that takes into account spaces of greater dimension (for example, turns and hinges).

Motion planning can be understood as searching for a path in the configuration space of an agent.

Random Planning: Probabilistic Road Maps (PRM)

One of the first general solutions to multidimensional planning problems is called a probabilistic roadmap . It borrows the ideas of the Navigation Mesh and the visibility graph, adding another component: randomness.

First, I’ll introduce some background information. We already know that the most complex aspects of planning in multidimensional spaces are to calculate the configuration space and then find the optimal path through this space.

PRM solves both of these problems by completely rejecting the idea of ​​calculating the configuration space and forgetting about the principle of optimality. With this approach, a visibility graph in space is randomly created using distance heuristics, and then a solution is searched for in this visibility graph. You can also make the assumption that we can relatively seamlessly perform collision checking on any agent configuration.

Here's what the whole algorithm looks like:

Алгоритм: PROBABALISTIC ROAD MAP (PRM)

• Создаём пустой граф G
• Добавляем в граф G узлы начала и цели.
• За N итераций:
  
  • Находим одну однородную случайную выборку конфигурационного пространства и называем её R. Для этого просто рассматриваем каждое измерение конфигурационного пространства как случайное число и генерируем ровно одну точку как список этих случайных чисел.
  • Если агент находится в коллизии при конфигурации R, то продолжаем.
  • В противном случае, добавляем R к графу G.
  • Находим все узлы в G, находящиеся в пределах расстояния d от R.
  • Для каждого узла N, соответствующего этому критерию
    
    • Пробуем разместить прямую линию без коллизий между R и N
    • Если у ребра отсутствуют коллизии, то добавляем его к G.
    • Выполняем планирование с помощью A* или алгоритма Дейкстры от начала до цели.
    
    
  
  

In short, at each stage we create a random point and connect it with the neighbors in the graph based on which neighboring nodes of the graph she “sees”, that is, if we are sure that a straight line can be drawn between any new node and neighbors in the graph .

We immediately see that this is very similar to the visibility graph algorithm, except that we never mention “for each obstacle” or “for each vertex”, because, of course, such calculations will be NP-complete.

Instead, the PRM considers only the structure of the random graph created by it and the collisions between neighboring nodes.

Properties of PRM

We have already said that the algorithm is no longer optimal and not complete. But what can we say about its performance?

The PRM algorithm is the so-called "probabilistically complete . ”This means that as the number of iterations N goes to infinity, the probability that PRM solves any solvable planning request equals one. This seems like a very shaky definition (it is), but in practice PRM converges to the right solution very quickly However, this means that the algorithm will have a random speed and may freeze forever without finding a solution.

PRM also has an interesting relationship with optimality. As the size of PRM (and the growth of N to infinity) increases, the number of possible paths increases ad infinitum, and the optimal path through PRM becomes the truly optimal path through the configuration space.

As you can imagine, due to its randomness, PRM can create very ugly, long and dangerous paths. In this regard, PRM is by no means optimal.

Like visibility graphs with Nav Mesh, fundamentally, PRMs are multi-query schedulers. They allow the agent to reuse a random graph efficiently for multiple scheduling requests. Level designers can also bake one PRM for each level.

Why an accident?

The most important trick of PRM (and other randomized algorithms) is that it represents the configuration space statistically, and not explicitly. This allows us to sacrifice the optimality of the solution for the sake of speed, making “fairly good” decisions where they exist. This is an incredibly powerful tool because it allows the programmer to decide how much work the scheduler needs to complete before returning the solution. This property is called the real-time execution algorithm property .

In essence, the complexity of PRM grows with an increase in the number of samples and a distance parameter d, and not with an increase in the number of dimensions of the configuration space. Compare this to A * or visibility graphs that spend exponentially more time as the dimension of the problem increases.

This feature allows PRM to quickly plan in hundreds of dimensions.

Since the invention of PRM, many different variants of the algorithm have been proposed that increase its efficiency, the quality of the paved path and ease of use.

Randomized Exploring Randomized Trees (RRT)

Sometimes PRM multitasking is not required. Quite often, it is better to just get from point A to point B without knowing anything about previous planning requests. For example, if the environment between scheduling requests changes, it is often better to simply reschedule from scratch than to recreate the stored information obtained from previous scheduling requests.

In such cases, we can change the idea of ​​creating random graphs, taking into account the fact that we want to only plan once the movement from point A to point B. One way to implement this is to replace the graph with a tree.

A tree is simply a special type of graph in which the nodes are arranged in “parent” and “child” so that each node in the tree has exactly one parent node and from zero or more children.

Let's see how our movement planning can be represented as a tree. Imagine an agent systematically exploring configuration space.

If the agent is in some state, then there are several other states to which it can go from the current (or, in our case, an infinite number of states). From each of these states he can go into other states (but will not go back, because he was already in the state from which he came).

If we store the states in which the agent was in as “parent” nodes, and all the states into which the agent goes from them as “child” nodes, then we can form a tree-like structure growing from the current state of the agent to all places, where the agent could potentially be located. Sooner or later, the agent tree will direct it to the state of the target and we will have a solution.

This idea is very similar to the A * algorithm, which systematically expands the states and adds them to the tree-like structure (from a technical point of view, into an oriented acyclic graph).

So can we randomly grow the tree from the initial configuration of the agent to achieve the configuration of the target?

Two classes of algorithms seek to solve this problem. Both were invented in the late 90s and early zero. One approach is “centric” - it selects a random node in the tree and grows in a random direction. This class of algorithms is called "EST", that is, "Expansive Space Trees" ("extensible spatial trees"). The second approach is “sample-oriented”: it starts with a random selection of nodes in space, and then grows the nearest node in the direction of this random sample. Algorithms of this type are called " RRT " ("Rapidly Exploring Randomized Trees", "randomized trees random research").

In general, RRT is much better than EST, but an explanation of the reasons is beyond the scope of this article.

Here's how RRT works:

Алгоритм: RAPIDLY EXPLORING RANDOMIZED TREE (RRT)

• Создаём пустое дерево T.
• Добавляем к T начальную конфигурацию агента.
• В течение N итераций, или пока не достигнута цель
  
  • Случайным образом делаем выборку для узла R.
  • Находим в T ближайший к R узел. Называем его K.
  • Делаем шаги по лучу от K до R на малую величину эпсилон, пока не выполнится следующее условие:
    
    • При наличии коллизии возвращаемся к созданию случайной выборки.
    • В противном случае добавляем к T новый узел в этой конфигурации.
    • Если мы достигли максимального расстояния d от K, то возвращаемся к созданию случайной выборки.
• Если узел цели теперь находится в пределах расстояния d от любого узла дерева, то у нас есть решение.

The figures above approximately show one step of the algorithm in the middle of its execution. We take a random sample (orange, r), find the node closest to it (black, k), and then add one or more new nodes that take a “step in the direction” of the random sample.

The tree will continue to grow randomly until it reaches the goal. From time to time, we will also randomly sample the target, eagerly trying to draw a straight line to it. In practice, the probability of a target falling into the sample will at best be in the range from 30% to 80%, depending on the clutter of the configuration space.

RRTs are relatively simple. They can be implemented in just a few lines of code (assuming that we can easily find the nearest node in the tree).

RRT Properties

You probably won't be surprised that the RRT algorithm is just probabilistically complete . It is not optimal (and in many cases is excessively non-optimal).


Robot manipulators are considered very multi-dimensional systems. In this case, we have two manipulators with seven hinges each, holding single-hinged wire cutters. The system is 15-dimensional. Modern studies of motion planning study such multidimensional systems.

Due to its simplicity, RRT is also usually extremely fast (at least for multidimensional systems). Using the fastest RRT variations, solutions for seven-dimensional or more multi-dimensional systems are found in milliseconds. When the number of measurements reaches tens, RRT usually surpasses all other schedulers in solving such problems. But it’s worth considering that the “fast” in the community of multidimensional planning researchers means a secondor so to complete the entire pipeline of actions in seven dimensions, or up to a minute with twenty or more dimensions. The reason for this is that RRT paths are often too terrible to use directly and must go through a lengthy pre-processing step. This can shock programmers using A *, which returns solutions to two-dimensional problems in milliseconds; but try to execute A * for the seven-dimensional task - it will never return the solution ever !

Variations of RRT

After the invention of the RRT algorithm and its huge success, many attempts were made to expand it to other areas or increase its performance. Here are some of the RRT variations worth knowing about:

RRTConnect- grows two trees from the beginning and from the goal, and tries to connect them with a straight line at random intervals. As far as I know, this is the fastest scheduler for tasks with a high number of dimensions. Here is a beautiful illustration of the RRT connect implementation I created (white - obstacles, blue - free space):


RRT * - invented in this decade. Guaranteed optimality through rebalancing the tree. Thousands of times slower than RRTConnect.

T-RRT — Attempts to create high-quality RRT paths by exploring the gradient of the cost function.

Constrained RRT - allows you to perform planning with arbitrary restrictions (such as restrictions on distance, cost, etc.). Slower than RRT, but not by much.

Kinodynamic rrt- performs planning in the space of input control signals, and not in the configuration space. Allows you to carry out planning for cars, carts, ships and other agents who can not arbitrarily change their turn. Actively used in the DARPA Grand Challenge. Much, much, MUCH slower than non-kinodynamic planners.

Discrete RRT is an implementation of RRT for meshes. In two-dimensional space it is comparable in speed to A *, in 3D and in multidimensional systems it is faster than it.

DARRT - invented in 2012. Implementing RRT for planning symbolic actions (previously considered A * scope).

Path cutting and optimization

Since randomized schedulers do not guarantee optimality, the trajectories they create can be quite terrible. Therefore, instead of using them directly for agents created by randomized schedulers, directories are often transferred to stages of complex optimization that increase their quality. Such optimization steps today take up most of the planning time of randomized planners. A seven-dimensional RRT may be required to return a possible path in just a few milliseconds, but it may take up to five seconds to optimize the final path.

In the general case, the trajectory optimizer is an algorithm that obtains the initial trajectory and the cost function, changing the initial trajectory so that it has the lowest cost. For example, if the cost function we need is to minimize the length of the path, then the optimizer for this function will take the original path and change this path so that it is shorter. This type of optimizer is called the Trajectory Shortcutter .

One of the most common and extremely simple path cutters (which can be called a “stochastic climb cutter”, Stochastic Hill Climbing Shortcutter) works as follows:

Алгоритм: Stochastic Hill Climbing Shortcutter

• В течение N итераций:
  • Берём две случайные точки на траектории T (называем их t1 и t2)
  • Если соединение прямой линией t1 и t2 не делает траекторию короче, то продолжаем.
  • В противном случае, пробуем соединить t1 и t2 прямой линией
    
    • Если можно найти прямую линию без коллизий, то срезаем траекторию T от t1 до t2, отбрасывая всё между ними
    
    
  
  

This trajectory cutter can be easily transformed by replacing the concept of “short path” with any other cost function (for example, distance from obstacles, smoothness, safety, etc.). Over time, the trajectory will fall into what is called the “local minimum” of the cost function. The length (or cost) of the trajectory will no longer decrease.

There are more sophisticated trajectory optimizers that work much faster than the climb I described. Such optimizers often use knowledge about the scope of the planning task to speed up work.

Planning path optimization

Another way to solve multidimensional traffic planning problems is to step aside from the idea of ​​“searching for space” to find a path, and instead focus directly on optimizing trajectories.

If it is true that we can optimize the trajectory so that it is shorter or meets some other criterion, is it possible to solve the whole problem using directly optimization?

There are a large number of motion planners using optimization to directly solve planning problems. Usually for this they represent the trajectory using a parametric model, and then intelligently change the parameters of the model until a local minimum is reached.

One way to implement this process is called gradient descent.. If we have a certain cost function C (T) , where T is the path, then we can calculate the gradient D_C (T) , which tells you how to change the given path in such a way as to minimize costs.

In practice, this is a very complex process. You can imagine it like this:

Алгоритм: Gradient Descent Trajectory Optimizer

1. Чем больше траектория проходит через препятствия, тем более она затратна.
2. Начинаем с прямой линии от агента до цели. Назовём её T_0.
3. Во всех точках, где траектория сталкивается с препятствиями, вычисляем направление, в котором точка наискорейшим образом покинет препятствие.
4. Представьте, что траектория - это эластичная резиновая лента. Теперь представьте, что мы тянем каждую точку в направлении, заданном на этапе 3.
5. Вытянем немного все точки согласно 4.
6. Повторяем, пока вся траектория не будет находиться вне коллизий.

Over time, the trajectory will gradually “push off” from obstacles, nevertheless remaining smooth. In the general case, such a scheduler cannot be complete or optimal , because as a strong heuristic, it uses the initial straight line hypothesis. However, it can be locally complete and locally optimal (and in practice it solves most problems).


Note that in the image, the gradients of the points represent the * negative * gradient of the cost function)

In practice, the optimization of trajectories as planning is a rather difficult and confusing topic, which is difficult to judge in this article. What does the calculation of the gradient of the trajectory really mean? What does perception of a trajectory as a rubber band mean? There are very complex answers to these questions related to variational analysis.

It’s just enough for us to know that path optimization is a powerful alternative to randomized and search planners for multi-dimensional traffic planning. Their advantages are exceptional flexibility, theoretical guarantees of optimality, extremely high path quality and relative speed.


CHOMP, used by the robot to raise the circle (Illustration from the work of Dragan et. Al )

In recent years, a lot of very fast track optimizers have appeared that have become strong competitors of RRT and PRM in solving multidimensional problems. One of them, CHOMP , uses gradient descent and a smart representation of obstacles using the distance field. Another, TrajOpt , presents obstacles in the form of convex sets and uses sequential quadratic programming techniques.

Important topics that we did not cover

In addition to what I said, there is still a whole world of theoretical movement planning. I’ll briefly talk about what else is there.

Nonholonomic planning

We considered only the case when an agent can move in any direction at any speed. But what if it is not? For example, a car cannot slide sideways, but must move forward and backward. Such cases are called “non-holonomic” planning tasks. This task has several solutions, but none of them is fast! A modern car planner can take up to a minute to calculate the average plan .

Restricted Planning

Nonholonomic planning refers to yet another set of tasks called “constrained planning tasks”. In addition to restrictions on movement, there may also be restrictions on the physical configuration of the agent, the maximum force used by the agent for movement, or the area in which the agent is limited by objects other than obstacles. In generalized planning with restrictions, there are also many solutions, but only a few are fast .

Time planning

We can add time to the plans as another dimension, so that agents can, for example, track a moving target or avoid moving obstacles. When implemented correctly, such techniques can produce surprising results. However, this problem remains intractable because the agent often cannot predict the future.

Hybrid planning.

What if our agent’s plan cannot be imagined in a single trajectory? What if an agent needs to interact along the way with other objects (and not just avoid them)? These types of tasks are usually referred to as “hybrid planning” - usually there is some abstract aspect associated with the geometric aspect of the task. For these types of tasks there are also no clear, universally accepted decisions.

conclusions

In this article we examined some basic concepts of motion planning and presented several classes of algorithms that solve the problem of moving an agent from point A to point B, from the simplest to the extraordinarily complex.

Modern progress in studies of motion planning has led to the fact that a wide range of previously unsolved problems can now be solved on personal computers (and potentially in video game engines).

Unfortunately, many of these algorithms are still too slow to use in real time, especially for cars, ships, and other vehicles that cannot move in all directions. All this requires further research.

I hope the article didn’t seem too complicated for you and you found something useful for yourself in it!

Here is a summary table of all the algorithms discussed in the article (it should be noted that only non-kinodynamic planning is taken into account here):