Work with the KOMPAS-3D API → Lesson 6 → Creating a circular arc
- Tutorial
We continue the series of articles on working with the KOMPAS-3D CAD API Sergey Norseev, software engineer at VNII Signal JSC, author of the book Development of Applications for KOMPAS in Delphi. The environment used is C ++ Builder. In previous lessons on the KOMPAS API Basics and Drawing Design, we assumed that KOMPAS was not running, in the Correct Connection to KOMPAS lesson, we checked that KOMPAS was already running and connected to it. In the lesson, the main inscription was analyzed, how to fill in the main inscription of the drawing. In the last lesson, Graphic primitiveswe began to draw the first geometric shapes. This article discusses various ways to construct a circular arc. In KOMPAS it can be built in three different ways. We will consider them all.

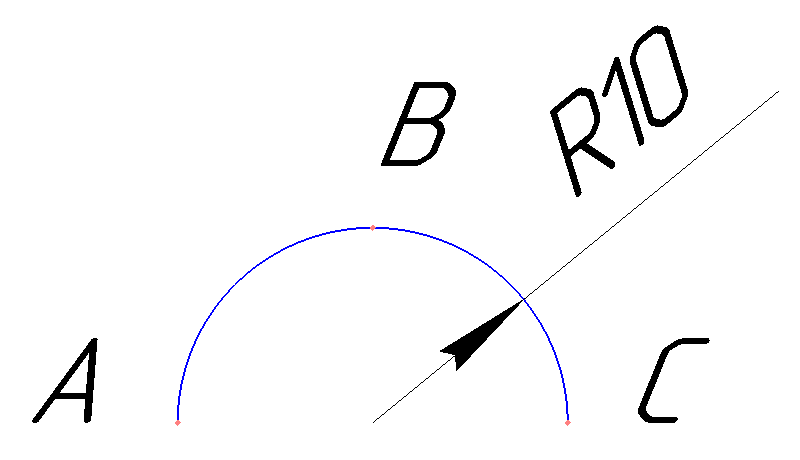
First, we will determine what we will build. For example, I propose to take a semicircle of radius 10 mm centered at a point with coordinates (100, 100) . This arc is shown in the figure below. (The picture is clickable). A, B and C are auxiliary points that are useful to us in describing various ways of constructing an arc.
The first method is based on the fact that you know the coordinates of points A, B and C , but the coordinates of the center are unknown. To draw an arc by three points method is used ksArcBy3Points interface ksDocument2D . The following is its prototype.
Line styles were discussed in a previous article in the series .
If successful, the method returns a pointer to the constructed arc, and in case of an error, the value is zero .
To build our arc, you need to determine the coordinates of the points. So, point A has coordinates (90, 100) , point B (100, 110) , point C (110, 100) . With such initial data, the ksArcBy3Points method should be called as shown below.
How to get a pointer to the ksDocument2D interface was described in previous articles in the series .
This method is based on the fact that you know the coordinates of the center of the arc and the angles of its ends. To construct the arc of this information, the method ksArcByAngle interface ksDocument2D . The following is a prototype of this method.
With the parameters xc , yc , rad and style , I think everything is clear. No questions should arise with them.
Parameters f1 and f2 specify the angles ( in degrees ) between the lines passing through the center of the arc and its end points, and the horizontal line. These angles are shown in the figure below.
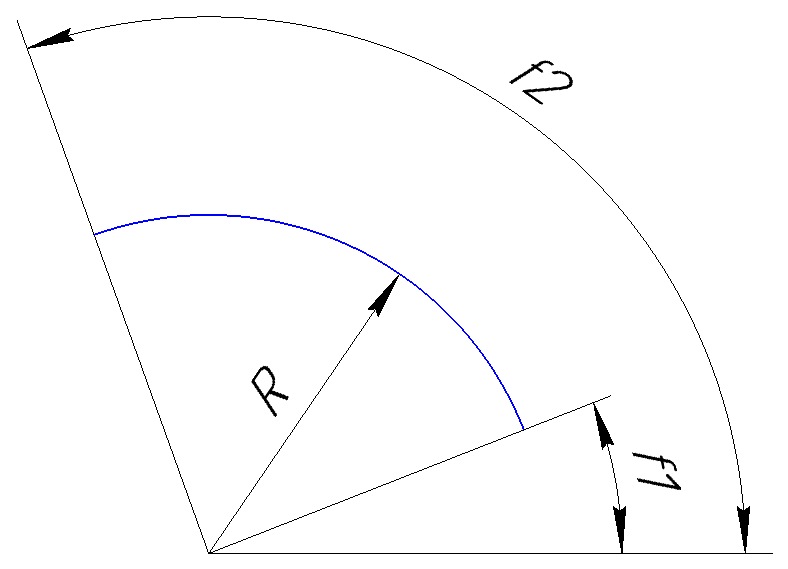
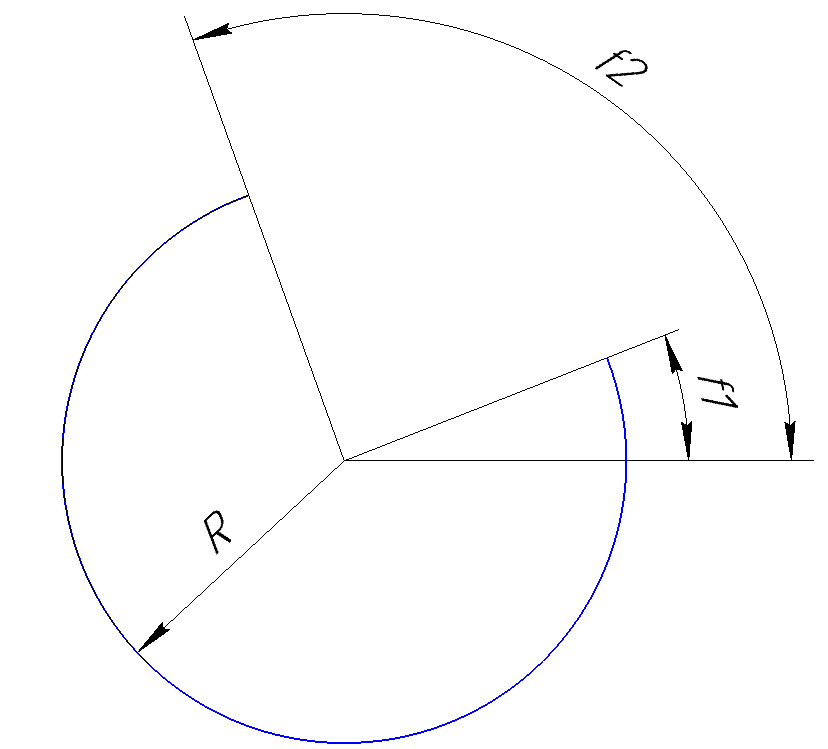
Now about the direction parameter . It sets the direction in which the arc should be drawn. If it is 1 , then the arc is built counterclockwise, if it is -1, then the arc is built clockwise. For example, the arc shown in the figure above is drawn counterclockwise, and the figure below shows an arc built with the same parameters, but clockwise.
If successful, the ksArcByAngle method returns a pointer to the constructed arc, and in case of an error, returns zero .
Let us return to our task of constructing an arc. To draw it counterclockwise, the angles must be specified as follows: f1 = 0 , f2 = 180 . To draw the same arc clockwise, the values of the angles must be interchanged (f1 = 180, f2 = 0) .
The arc construction code is given below.
This method is based on the fact that you know the coordinates of the center of the arc and the coordinates of the end points of the arc. To construct the arc of this information, the method ksArcByPoint interface ksDocument2D . The following is a prototype of this method.
This method is very similar to the ksArcByAngle method discussed earlier . The only difference is that the end points are not set by angles, but by coordinates.
If successful, the ksArcByPoint method returns a pointer to the arc, and in case of an error, returns zero .
Below is the code to call this method to build our arc.
An attentive reader must have noticed that the parameters of the ksArcByPoint method are redundant. Why? Is it really an API creators mistake? Not really. You just need to correctly understand the purpose of the points (x1, y1) and (x2, y2) . According to the KOMPAS documentation:
x1, y1 - coordinates of the starting point of the arc,
x2, y2 - coordinates of the end point of the arc.
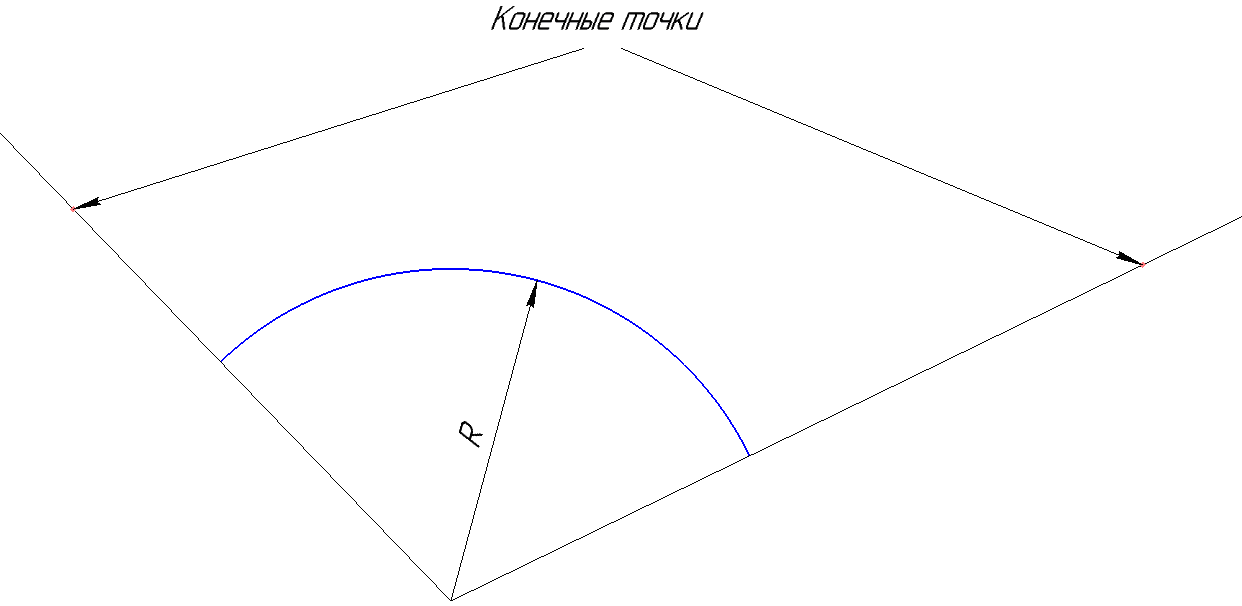
Such an incorrect description creates confusion. In fact, the points (x1, y1) and (x2, y2) may not belong to the arc. They do not specify the position of the end points, but the orientation of the vector on which they are located. Moreover, the beginning of this vector is in the center of the arc. The figure below illustrates this more clearly.
Based on this, the arc we are considering can be constructed using the code below.
Please note: the end points do not coincide with points A and C , but the arc is still correctly constructed.
Conclusion
In this article, we examined various ways of constructing a circular arc. Which one to use, decide for yourself. But I think that your decision will be determined by the information about the arc that you have at a given time.
To be continued, follow the news of the blog.
 Sergey Norseev, author of the book "Application Development for COMPAS in Delphi."
Sergey Norseev, author of the book "Application Development for COMPAS in Delphi."

Formulation of the problem
First, we will determine what we will build. For example, I propose to take a semicircle of radius 10 mm centered at a point with coordinates (100, 100) . This arc is shown in the figure below. (The picture is clickable). A, B and C are auxiliary points that are useful to us in describing various ways of constructing an arc.

At three points
The first method is based on the fact that you know the coordinates of points A, B and C , but the coordinates of the center are unknown. To draw an arc by three points method is used ksArcBy3Points interface ksDocument2D . The following is its prototype.
long ksArcBy3Points ( double x1, //Координаты первой точки
double y1,
double x2, //Координаты второй точки
double y2,
double x3, //Координаты третьей точки
double y3,
long style);//Стиль линии
Line styles were discussed in a previous article in the series .
If successful, the method returns a pointer to the constructed arc, and in case of an error, the value is zero .
To build our arc, you need to determine the coordinates of the points. So, point A has coordinates (90, 100) , point B (100, 110) , point C (110, 100) . With such initial data, the ksArcBy3Points method should be called as shown below.
Document2D->ksArcBy3Points( 90 , 100, //Точка А
100, 110, //Точка B
110, 100, //Точка C
1); //Cтиль линии
How to get a pointer to the ksDocument2D interface was described in previous articles in the series .
Center and corners
This method is based on the fact that you know the coordinates of the center of the arc and the angles of its ends. To construct the arc of this information, the method ksArcByAngle interface ksDocument2D . The following is a prototype of this method.
long ksArcByAngle ( double xc, //Координаты центра
double yc,
double rad, //Радиус
double f1, //Углы
double f2,
short direction, //Направление отрисовки
long style); //Стиль линии
With the parameters xc , yc , rad and style , I think everything is clear. No questions should arise with them.
Parameters f1 and f2 specify the angles ( in degrees ) between the lines passing through the center of the arc and its end points, and the horizontal line. These angles are shown in the figure below.

Now about the direction parameter . It sets the direction in which the arc should be drawn. If it is 1 , then the arc is built counterclockwise, if it is -1, then the arc is built clockwise. For example, the arc shown in the figure above is drawn counterclockwise, and the figure below shows an arc built with the same parameters, but clockwise.

If successful, the ksArcByAngle method returns a pointer to the constructed arc, and in case of an error, returns zero .
Let us return to our task of constructing an arc. To draw it counterclockwise, the angles must be specified as follows: f1 = 0 , f2 = 180 . To draw the same arc clockwise, the values of the angles must be interchanged (f1 = 180, f2 = 0) .
The arc construction code is given below.
Document2D->ksArcByAngle( 100, 100, //Координаты центра
10, //Радиус
0, 180, //Углы
1, //Против часовой стрелки
1); //Cтиль линии
Center and end points
This method is based on the fact that you know the coordinates of the center of the arc and the coordinates of the end points of the arc. To construct the arc of this information, the method ksArcByPoint interface ksDocument2D . The following is a prototype of this method.
long ksArcByPoint ( double xc, //Координаты центра
double yc,
double rad, //Радиус
double x1, //Координаты первой конечной точки
double y1,
double x2, //Координаты второй конечной точки
double y2,
short direction, //Направление
long style); //Стиль линии
This method is very similar to the ksArcByAngle method discussed earlier . The only difference is that the end points are not set by angles, but by coordinates.
If successful, the ksArcByPoint method returns a pointer to the arc, and in case of an error, returns zero .
Below is the code to call this method to build our arc.
Document2D->ksArcByPoint( 100, 100, //Координаты центра
10, //Радиус
110, 100, //Точка C
90 , 100, //Точка A
1, //Против часовой стрелки
1); //Стиль линии
An attentive reader must have noticed that the parameters of the ksArcByPoint method are redundant. Why? Is it really an API creators mistake? Not really. You just need to correctly understand the purpose of the points (x1, y1) and (x2, y2) . According to the KOMPAS documentation:
x1, y1 - coordinates of the starting point of the arc,
x2, y2 - coordinates of the end point of the arc.
Such an incorrect description creates confusion. In fact, the points (x1, y1) and (x2, y2) may not belong to the arc. They do not specify the position of the end points, but the orientation of the vector on which they are located. Moreover, the beginning of this vector is in the center of the arc. The figure below illustrates this more clearly.

Based on this, the arc we are considering can be constructed using the code below.
double xc = 100;
double yc = 100;
Document2D->ksArcByPoint( xc, yc, //Координаты центра
10, //Радиус
xc+1, yc, //Первая конечная точка
xc-1, yc, //Вторая конечная тока
1, //Против часовой стрелки
1); //Стиль линии
Please note: the end points do not coincide with points A and C , but the arc is still correctly constructed.
Conclusion
In this article, we examined various ways of constructing a circular arc. Which one to use, decide for yourself. But I think that your decision will be determined by the information about the arc that you have at a given time.
To be continued, follow the news of the blog.
 Sergey Norseev, author of the book "Application Development for COMPAS in Delphi."
Sergey Norseev, author of the book "Application Development for COMPAS in Delphi."