Genetic programming. ELTRUT problem
Wandering around the Internet, he became interested in such a thing as genetic programming . In a nutshell, it is the automatic creation of programs that fulfill a particular goal, in accordance with the principle of natural selection. That is, at first a generation of “creatures” -programs is randomly created that are sorted according to different criteria (proximity to achieving the goal), then some of them mutate (also by chance), some die out and some are replaced by new random creatures.
Thus, the most worthy creatures continue their work and give birth to descendants, and the weakest ones are eliminated in the selection process. Several experiments and their results are under the cut.
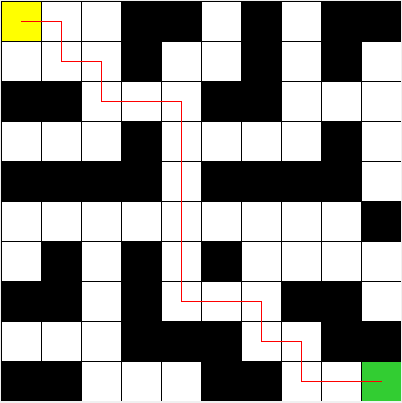
As a test of the pen, I decided to teach the creatures (we will call them that because the term “program” is too loud for this case) to look for a path in the maze, as in the picture above. I must say right away that in this case, the goal was not to use genetic engineering to create a creature that would find a path in an arbitrary maze, but to find a path in one specific maze, so that the creatures did not have sense organs. After some thought, it was decided to use a simple set of commands that can easily mutate and be executed by the creature. So, our “program” or “genome” is just a set of commands in which direction the creature should move. In addition, a loop has been added that can repeat a section of a program several times. A genome can be, for example, like this:

Here the FOR (IxT) command means that the next I instructions will be executed T times. A creature with such a genome will go 2 cells to the right, then 2 cells down and again 2 cells to the right.
Now let's take care of our being, which is essentially an interpreter of the genome. Each of our creatures will have a “name”, or an identifier by which we will later recognize it, a “genome” by which our creature will act, Step method, by which the creature will execute the next gene (we’ll check if it walks creature through walls), the Fitness function, which will determine how close the creature is to the finish cell, and the Mutate method, which will change part of the genome. About mutations a little later, but for now let's see how our cute little square performs our test program:
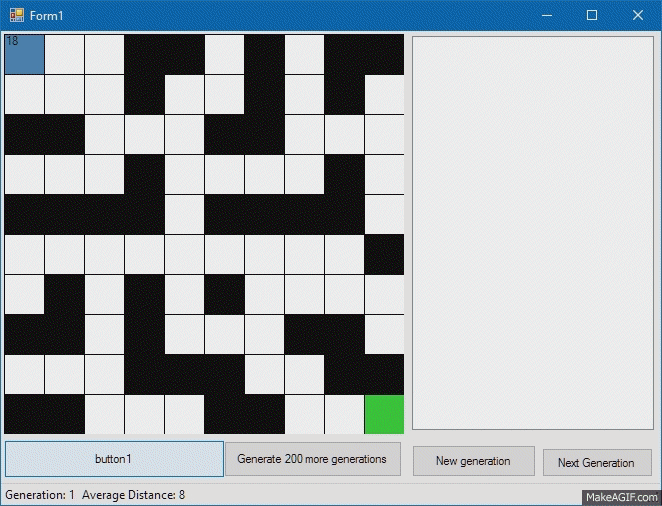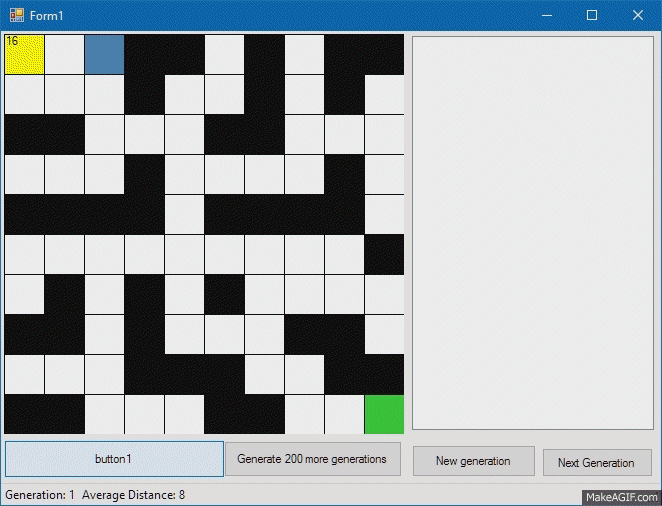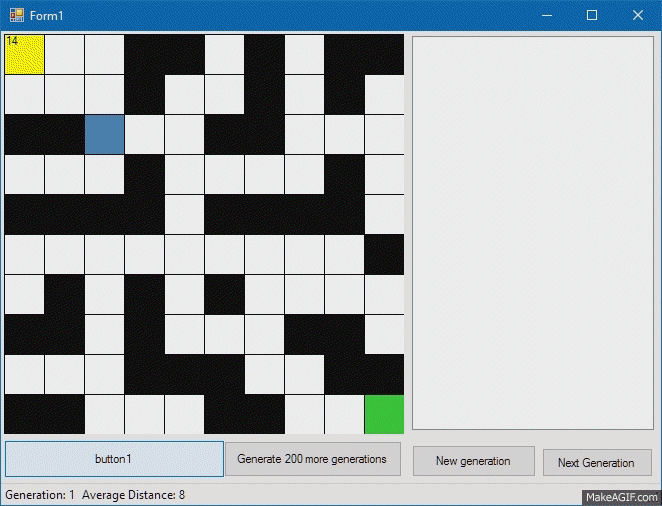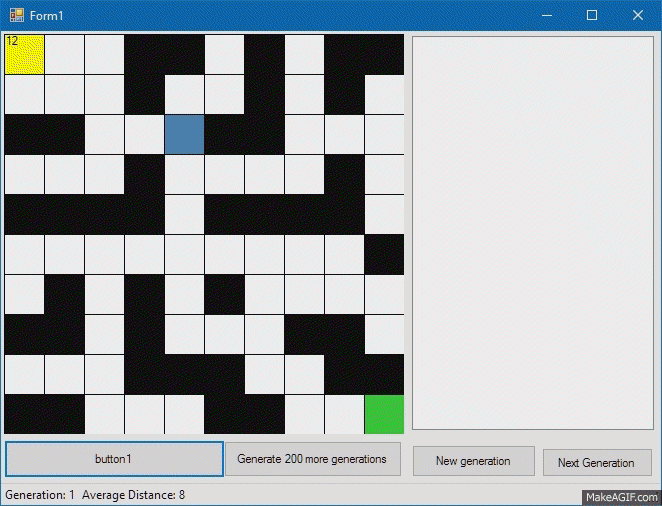
Fitness, or the creature’s compliance with our requirements, will be considered as the sum of the differences in the coordinates of the finish and the creature. So, the creature with the smallest distance to the target will be the most suitable.
The creatures we have will evolve generation after generation, 100 creatures each. Within each generation, we will repeat the same steps:
By the method of poking, we choose this ratio: the top 10 do not change, the next 60 mutate, the remaining 30 die out. We try, on the 292 generation we get the result: The
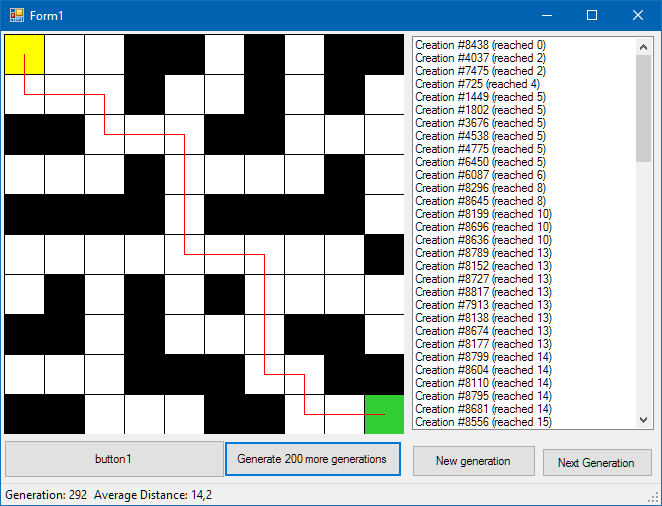
genome of our winner is this: As you can see, the creature often stomps in one place, which, in general, is not very good. Let’s try to take into account the length of the genome. But let us put it in second place in importance after the distance to the finish line, so that it doesn’t turn out that the short programs of 2-3 genes that are at the start are better than those that reach closer to the target, but have a long genome. By the method, again, poking, we try the formula: Now the search for a solution takes a little longer. At the 335th generation, we get exactly the same result, but with the following genome:
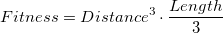
Actually, there is still much to be improved, but the problem has been solved, with acceptable quality and with reasonable labor costs. I intentionally do not provide my code in connection with its incompleteness. Therefore, with a clear conscience, we can proceed to the topic in the title.
In 2012, a graduate of the University of California, Benjamin Bush, was engaged in genetic algorithms and, in particular, the so-called ELTRUT problem. The essence of the task is this: there is a bitmap image, find the sequence of commands for the Logo turtles , which will draw a similar image. Here is a video where everything is pretty easily explained:
In short, Benjamin offers the following solution: we abandon the simple linear genome in favor of the two-dimensional. Why? Because the two-dimensional genome has redundancy, so not every mutation will provoke a fundamental change in the genome. Benjamin also offers an interesting form of representation of the genome: each pixel of the image is associated with a gene that points in which direction and at what distance the turtle should go if it hits this point, and if it needs to draw a line. Visually, the genome can be displayed as follows:
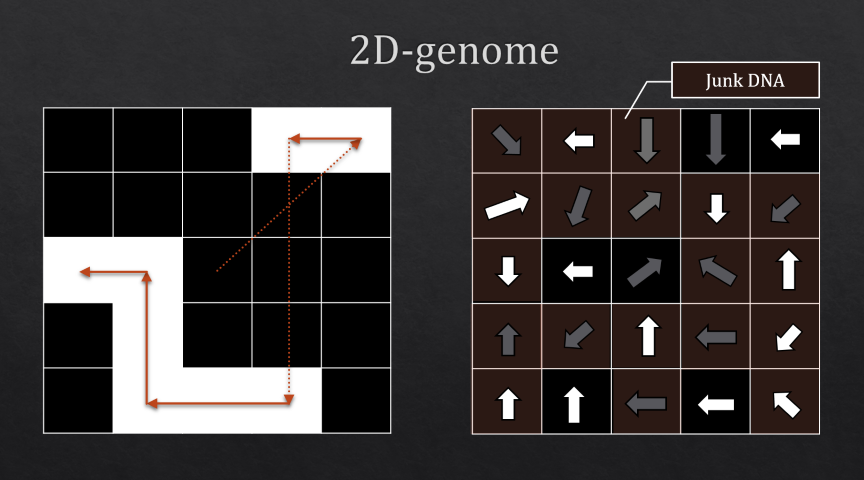
Here, the excess genome is highlighted in brown. It can be seen that in almost 80% of mutations, changes in the behavior of the turtle will not occur. In addition, when solving this problem, it is proposed to use “sexual reproduction,” or crossingover: two creatures of the previous generation exchange genes to get descendants. Next, we will talk about the three-dimensional genome and optimization of the algorithm, but I did not want to do optimization, and the three dimensions are a little too familiar with genetic algorithms, so I decided to focus on the implementation of a simplified algorithm.
So, similarly to the previous task, in each generation we will have 100 creatures. In each generation we will:
How will we determine the degree to which creatures fit? For each correctly drawn pixel, we will essentially accrue a certain number of points, for each incorrectly drawn pixel we will fine. If where the pixel is not painted over, and it should not be painted over, do not change the count. Total, an approximate algorithm for scoring:
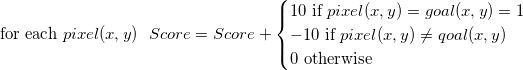
Immediately solve another problem (it should be solved by the three-dimensional genome): if the turtle stands on the pixel where it was already, then the program will loop. Therefore, we make sure that stepping on the visited pixel, the turtle stops. At the same time, we will not chase the poor reptile until blue in the face.
So, we try. 5x5 image, not very complicated, can we get the result?
Not bad, but how will the program handle a slightly larger image, for example, 8x8?
The video is greatly accelerated (the previous one is also accelerated, but slightly). 2000 generations have not given the right result. You could try to continue, but as you can see on the schedule, about 1,000 generations did not change, so this is unlikely to solve the problem. Well, a dislike for optimization did the trick: it took about 2 hours on an 8x8 image on my computer. So, the experiment is recognized partially failed.
Thanks for your time, I hope this article seems interesting to someone.
Thus, the most worthy creatures continue their work and give birth to descendants, and the weakest ones are eliminated in the selection process. Several experiments and their results are under the cut.

First samples. Walk through the maze
As a test of the pen, I decided to teach the creatures (we will call them that because the term “program” is too loud for this case) to look for a path in the maze, as in the picture above. I must say right away that in this case, the goal was not to use genetic engineering to create a creature that would find a path in an arbitrary maze, but to find a path in one specific maze, so that the creatures did not have sense organs. After some thought, it was decided to use a simple set of commands that can easily mutate and be executed by the creature. So, our “program” or “genome” is just a set of commands in which direction the creature should move. In addition, a loop has been added that can repeat a section of a program several times. A genome can be, for example, like this:

Here the FOR (IxT) command means that the next I instructions will be executed T times. A creature with such a genome will go 2 cells to the right, then 2 cells down and again 2 cells to the right.
Now let's take care of our being, which is essentially an interpreter of the genome. Each of our creatures will have a “name”, or an identifier by which we will later recognize it, a “genome” by which our creature will act, Step method, by which the creature will execute the next gene (we’ll check if it walks creature through walls), the Fitness function, which will determine how close the creature is to the finish cell, and the Mutate method, which will change part of the genome. About mutations a little later, but for now let's see how our cute little square performs our test program:

Fitness, or the creature’s compliance with our requirements, will be considered as the sum of the differences in the coordinates of the finish and the creature. So, the creature with the smallest distance to the target will be the most suitable.
Evolution
The creatures we have will evolve generation after generation, 100 creatures each. Within each generation, we will repeat the same steps:
- Checking creatures for compliance (calculation Fitness);
- Sort creatures by increasing distance to the target;
- Depending on the position in the list:
- either we will not change the creature, with the assumption that it is already good enough, and there is no need to spoil it;
- either change the genome: delete, add, change part of the genes;
- either replace with a new random creature, while the old "dies out" as unworthy of procreation.
By the method of poking, we choose this ratio: the top 10 do not change, the next 60 mutate, the remaining 30 die out. We try, on the 292 generation we get the result: The

genome of our winner is this: As you can see, the creature often stomps in one place, which, in general, is not very good. Let’s try to take into account the length of the genome. But let us put it in second place in importance after the distance to the finish line, so that it doesn’t turn out that the short programs of 2-3 genes that are at the start are better than those that reach closer to the target, but have a long genome. By the method, again, poking, we try the formula: Now the search for a solution takes a little longer. At the 335th generation, we get exactly the same result, but with the following genome:
Y_INC; X_INC; Y_INC; FOR_2x3; X_INC; Y_INC; FOR_1x4; X_DEC; FOR_2x3; Y_INC; X_INC; Y_DEC; Y_INC; FOR_2x4; Y_INC; X_INC; Y_INC; FOR_2x4; X_DEC; X_INC; X_INC;
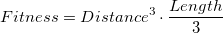
FOR_2x4; X_INC; Y_INC; FOR_2x3; Y_INC; X_INC; Y_DEC; Y_INC; FOR_2x4; Y_INC; X_INC;
Actually, there is still much to be improved, but the problem has been solved, with acceptable quality and with reasonable labor costs. I intentionally do not provide my code in connection with its incompleteness. Therefore, with a clear conscience, we can proceed to the topic in the title.
ELTRUT problem
In 2012, a graduate of the University of California, Benjamin Bush, was engaged in genetic algorithms and, in particular, the so-called ELTRUT problem. The essence of the task is this: there is a bitmap image, find the sequence of commands for the Logo turtles , which will draw a similar image. Here is a video where everything is pretty easily explained:
In short, Benjamin offers the following solution: we abandon the simple linear genome in favor of the two-dimensional. Why? Because the two-dimensional genome has redundancy, so not every mutation will provoke a fundamental change in the genome. Benjamin also offers an interesting form of representation of the genome: each pixel of the image is associated with a gene that points in which direction and at what distance the turtle should go if it hits this point, and if it needs to draw a line. Visually, the genome can be displayed as follows:
Here, the excess genome is highlighted in brown. It can be seen that in almost 80% of mutations, changes in the behavior of the turtle will not occur. In addition, when solving this problem, it is proposed to use “sexual reproduction,” or crossingover: two creatures of the previous generation exchange genes to get descendants. Next, we will talk about the three-dimensional genome and optimization of the algorithm, but I did not want to do optimization, and the three dimensions are a little too familiar with genetic algorithms, so I decided to focus on the implementation of a simplified algorithm.
So, similarly to the previous task, in each generation we will have 100 creatures. In each generation we will:
- Cross 50 of the best creatures and replace the 50 worst with their descendants;
- Change one gene for each creature except the top 10;
- If the creature has already completed its task, then it will not mutate.
How will we determine the degree to which creatures fit? For each correctly drawn pixel, we will essentially accrue a certain number of points, for each incorrectly drawn pixel we will fine. If where the pixel is not painted over, and it should not be painted over, do not change the count. Total, an approximate algorithm for scoring:
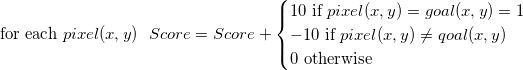
Immediately solve another problem (it should be solved by the three-dimensional genome): if the turtle stands on the pixel where it was already, then the program will loop. Therefore, we make sure that stepping on the visited pixel, the turtle stops. At the same time, we will not chase the poor reptile until blue in the face.
So, we try. 5x5 image, not very complicated, can we get the result?
For 61 generations, the program found an algorithm for the turtle:
Rotate 270
Forward 1
PenUp
Rotate -146.3
Forward 3.6
PenDown
Rotate -123.7
Forward 4
Rotate 270
Forward 4
Rotate 270
Forward 4
Rotate 270
Forward 4
Not bad, but how will the program handle a slightly larger image, for example, 8x8?
The video is greatly accelerated (the previous one is also accelerated, but slightly). 2000 generations have not given the right result. You could try to continue, but as you can see on the schedule, about 1,000 generations did not change, so this is unlikely to solve the problem. Well, a dislike for optimization did the trick: it took about 2 hours on an 8x8 image on my computer. So, the experiment is recognized partially failed.
Thanks for your time, I hope this article seems interesting to someone.
