A diffraction pattern was found in the distribution of prime numbers, approximately as in quasicrystals.
In March 2016, Robert J. Lemke-Oliver and Kannan Soundararajan from Stanford University opened a new pattern in the distribution of prime numbers. It turned out that primes are specifically distributed over the numerical space. For more, see the translation of the article “Structure and randomness of prime numbers” on Habré.
Experts from other fields, including chemistry, have joined the study of the topic. And successful. Professor of Theoretical Chemistry Salvatore Torquato with numbers theorist Matthew de Courcy-Ayrlend find new templatesin the distribution of prime numbers, which were previously unknown. It turned out that the distribution of prime numbers forms a fractal-like diffraction pattern, somewhat similar to the diffraction pattern in exotic quasicrystals.
Professor Torcuato specializes in the study of patterns in the structures of physical systems, such as crystals and colloids. The standard way to study the structure is X-ray diffraction. Messy molecules in liquids or gas reflect rays in all directions without creating a noticeable pattern. But symmetrically located atoms in a crystal synchronously reflect light waves, creating periodic bright spots of pronounced diffraction ( Bragg peaks ). Analysis of Bragg peaks makes it possible to understand the internal structure of a crystal or other material that creates such a picture.
So, in new scientific articles Torcuato and others ( 1 , 2 , 3) it is shown that the detected ordered structure in the distribution of prime numbers is nothing more than a fractal-like diffraction pattern, approximately as in quasicrystals.
The Bragg peak pattern on a prime-number lattice is similar to quasicrystals, but still differs from them. Torcuato says that primes as a physical system "are a completely new category of structure." The researchers called this new fractal-like pattern “effective limit-periodicity”.
The drawing consists of a periodic sequence of bright vertices that reflect the most common prime number intervals: they are all odd (except 2), many next to each other. The brightest peaks (pairs separated by two digits) alternate at regular intervals with less bright peaks, reflecting prime numbers separated by six digits. Between them are even dimmer peaks corresponding to more distant pairs of prime numbers, etc. All this is an infinite number of Bragg peaks placed inside each other.

A similar structure of the Bragg peaks was observed earlier - in diffraction patterns of quasicrystals.
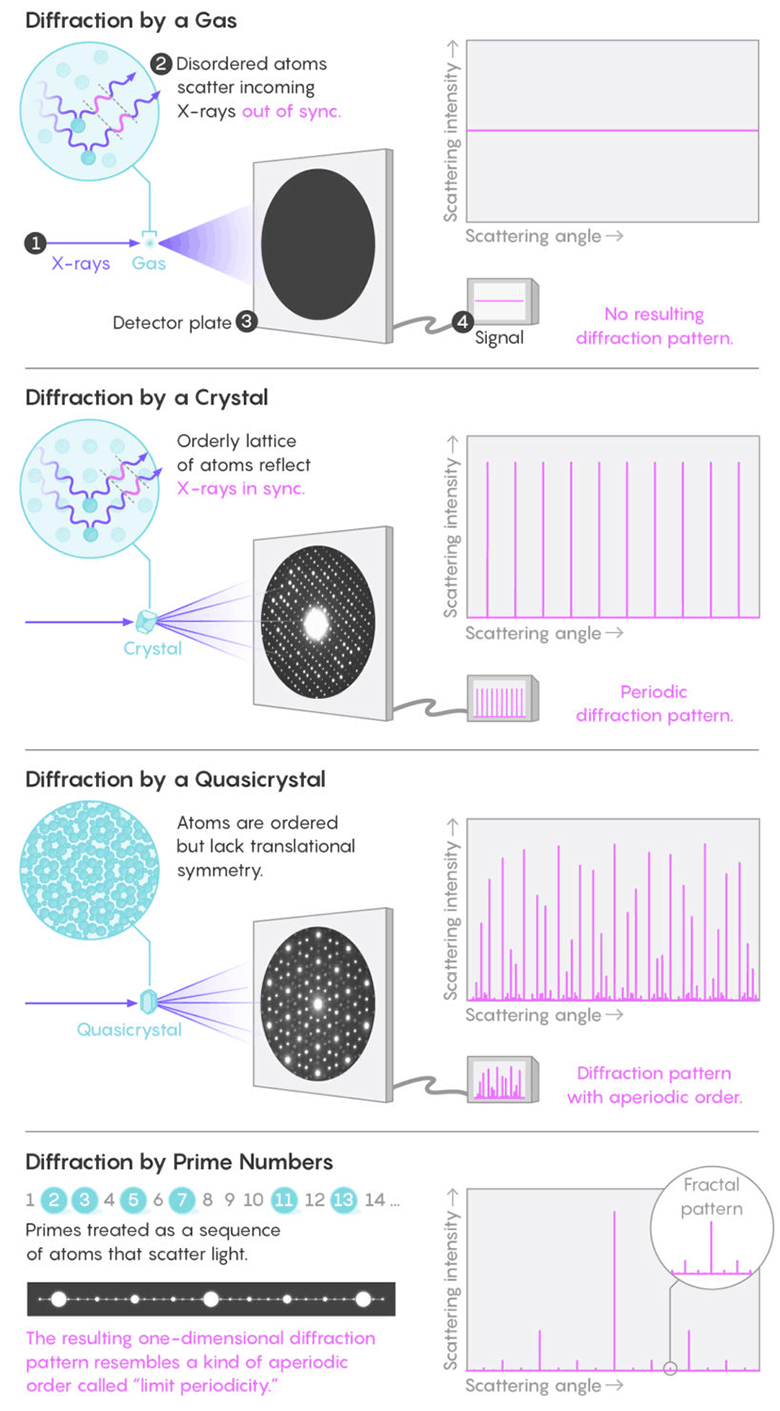
Messy molecules in liquids or gas reflect rays in all directions without creating a noticeable pattern. But symmetrically located atoms in a crystal synchronously reflect light waves, creating periodic bright spots of pronounced diffraction. As it turned out, the pattern of distribution of primes forms a fractal diffraction pattern, approximately like that of quasicrystals
Quasicrystals are strange materials found in the 1980s. They are characterized by the symmetry forbidden in classical crystallography and the presence of long-range order. Mathematical model of quasicrystals are aperiodic mosaics of the famous Penrose mosaics type.. There is no translational symmetry in such mosaics, repeatability and quasicrystallinity (fifth order symmetry) are present.
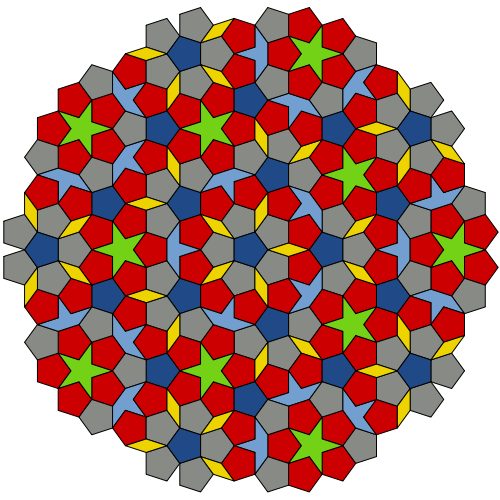
Penrose mosaic fragment of type P1 (of six types of tiles)
In the case of prime numbers, the distances between the peaks are proportional parts of each other, unlike the irrationally spaced Bragg peaks of the quasicrystals. “Prime numbers actually suggest a completely different state of particle positions, similar to quasicrystals, but not like quasicrystals,” said Torcuato.
The discovery of the diffraction pattern cannot be called a breakthrough discovery for the theory of numbers, because the main part of these patterns has already been described earlier, only by other mathematical methods (not through the diffraction of quasicrystals). So, using the diffraction pattern, it is possible to predict the “twins” of types 17 and 19 - this is the mathematical equivalent of the first Hardy-Littlewood hypothesis.regarding the existence of tuples of prime numbers on a given segment of the number line. One of the rules prohibits triplets from consecutive odd numbers after {3, 5, 7}. The same explains why the next bright peak of Bragg in the diffraction pattern corresponds to numbers divided by six digits rather than four.
A new scientific work is just a fresh look at the problem of uniform distribution of prime numbers and an easier way to derive a certain “unified law” for them. In addition, this is an unusual way to analyze a mathematical problem from the point of view of crystallography, namely from the point of view of a relatively young field of research called the “aperiodic order”, which studies non-repetitive models and lies at the intersection of crystallography, dynamic systems, harmonic analysis and discrete geometry. This branch of science grew after the discovery of quasicrystals, when it became clear that the old methods did not work here.
The distribution of prime numbers resembles a special aperiodic order known since the 1950s. It is called limit periodicity. In such systems, periodic intervals are nested in an infinite hierarchy, so that in any interval the system contains parts of patterns that repeat only in a larger interval, as in the Taylor-Sokolar tile.

Taylor-Sokolar Tile
Theoretical calculations show that the extremely periodic phases of a substance should be able to form in nature, and such systems may have unusual properties. But no one thought to associate the limiting periodicity with prime numbers. Now we know that there is such a connection, and prime numbers demonstrate a new kind of limiting periodicity - the “effective” limiting periodicity, because the synchronicity in the distances between primes throughout the system is observed only statistically.
The question arises: how can regularities in the distribution of primes affect the strength of cryptographic algorithms?
“I get really a lot of letters on this topic. Although this is an interesting study, it is not related to cryptography, - wroteIn his blog, the famous cryptographer Bruce Schneier. - Cryptographers are not interested in the search for prime numbers or even their distribution. The persistence of RSA-type public-key cryptography algorithms is associated with the difficulty of factoring large composite numbers, which are the product of prime numbers. This is a completely different matter. ”
So despite the progress in studying the distribution of primes, there is no need to worry about the strength of crypto-cipher.

