Introduction to discrete-oriented polyhedra for collision detection

Collision detection of virtual objects is a pretty significant part for visualization tasks.

Task

And the task is to determine whether two objects collided (collide) or not.
The difficulty lies in the fact that when testing visualization primitives directly with other primitives, collision calculation takes unreasonably large resources, especially with a huge number of objects involved in the simulation.

To facilitate such calculations and not to check directly between visualization primitives (which takes the longest time), bounding volume technologies were invented that allow describing visualization objects in such a way that collision checking does not take up such significant resources, albeit with a small loss of accuracy.

In other words, bounding volumes are simple geometric shapes that fit more complex objects.

Bounding volumes

The most popular limiting volumes:
- Sphere.
- The bounding box, aligned on the coordinate axes (Axis-aligned bounding boxes - AABB, excuse me for the translation).
- Object-oriented bounding boxes (OBB)
- Discrete-oriented polyhedra. (Discrete oriented polytopes - k-DOPs)
- and others.


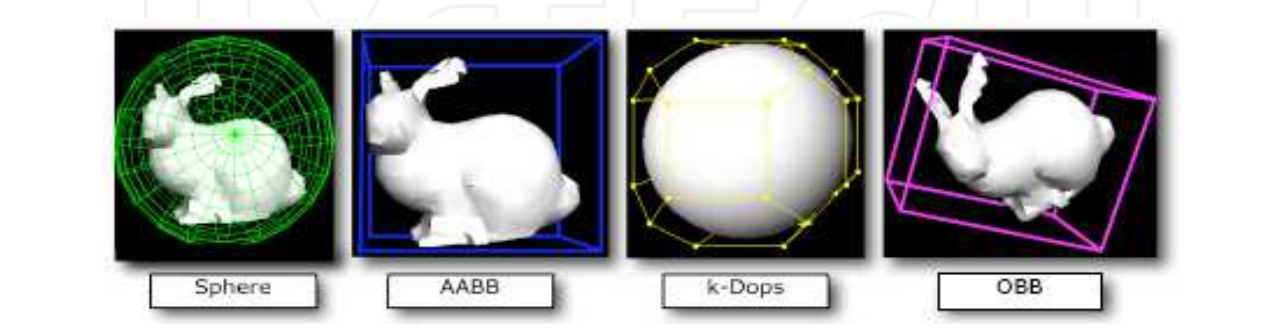
Figure 1. Overview of BV.

k-dop

Each of them has a number of advantages and disadvantages, but dwell on k-DOP.


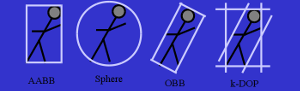
Figure 2. It is intelligible about BV.

Discrete-oriented polyhedra are a predetermined number of bounding planes and their orientation. K in the name describes the number of such planes.
For example, two-dimensional 4-DOP is an ordinary square describing a certain two-dimensional object. In fact, AABB is a special case of k-DOP.

Two-dimensional AABB is the same square as 4-DOP.
And three-dimensional AABB is the same cube as 6-DOP.

But k-DOP can also use more planes. And, as was said, the orientation of such planes is selected in advance and does not change.

The orientations of the planes are determined through direction vectors, the normals of which are bounded by the set {-1, 0, 1}.

For example, for a normal square, 4 planes with directions are needed: (0, 1), (1, 0).
Here are described the directions of two planes, but which limit the square from the bottom, top, left and right. Although there are 4 planes in total, it sometimes happens that they also write like this: (0, ± 1), (± 1, 0)

These normals can greatly simplify the calculations.

Structure

k-DOP is described only by minimum and maximum intervals (slabs) or distances. Two values ​​on one plane, which in the end is quite simple to process and store.


Figure 3. Intervals in k-DOP.

For example, for a square, as we remember, you need 4 planes (k = 4). Therefore, 2 (k / 2) minimum and 2 maximum values ​​are required.


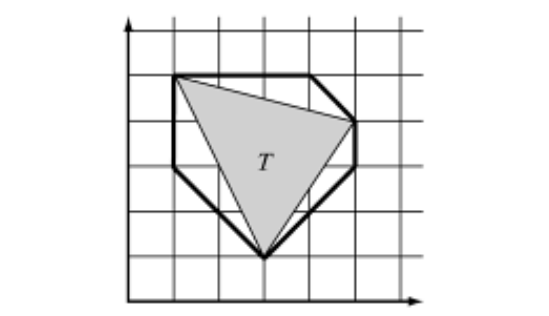
Figure 4. 8-DOP describing the triangle.

In Figure 4, a triangle with coordinates (3, 1), (5, 4), (1, 5) is described using 8-DOP, i.e., eight planes and with direction vectors (1, 0), (0, 1), (1, 1), (1, -1).

Let's count the intervals describing this polyhedron.

Take the first plane with the direction (1, 0) and multiply by the coordinates:
3 * 1 + 1 * 0 = 3
5 * 1 + 4 * 0 = 5
1 * 1 + 5 * 0 = 1

The minimum value here is 1, and the maximum 5.
The plane (1, 0) is determined by the values ​​1 and 5.
For the plane (0, 1), the same values ​​are 1 and 5.
For (1, 1) - 4 and 9.
For (1, -1) - -4 and 2.

Crossing check

If at least one plane does not intersect, then the entire structure also does not intersect.

Only if all intervals / planes intersect, then the k-DOP structure itself intersects. But it should be noted that the described object may not intersect.

Therefore, it is said that if k-DOP structures of two objects collide, then their described objects can collide.

bool overlapped (const KDop & a, const KDop & b, unsigned k)
{
    for (unsigned i = 0; i <k / 2; ++ i)
    {
        if (a.min [i]> b.max [i] || a.max [i] <b.min [i])
        {
            return false;
        }
    }
    return true;
}

Bounding Volume Hierarchy

As it turned out, the use of bounding volumes makes it easier to check for collisions, but it loses a bit of accuracy.

Therefore, for simple objects, in order to exclude unnecessary checks, they first test their bounding volumes, like AABB or k-DOP, and after that they switch to primitives.
But with complexly structured objects, hierarchies of bounding volumes are used. Often these are just binary trees, where the nodes define some kind of object or part of the object, limited by some volume.


Fig 5. The tree of objects.

The use of such trees is necessary to reduce the number of calculations.
Obviously, if a collision check is performed directly on objects, it may take too much time. The use of limiting volumes makes this task a little easier. And the union of limiting volumes into a hierarchical system makes it possible to exclude obviously disjoint parts of an object.

Usually creating a tree occurs in one of three ways.

A complex object (a root node) is divided into less complex objects (child nodes). For example, until the objects run out or until some condition is fulfilled. (top down method)

Simple objects (nodes) are combined into more complex ones until one complex root object (bottom up method) remains.

Or adding an object to an already generated tree (insertion method).

With such a balanced tree, the search complexity is equal to the complexity of other balanced binary search trees - O (logN).

The most interesting question is how to divide an object into children.
The criterion for comparing parts of an object to fit in a left or right subtree may vary.

The simplest is to simply divide the space in half: all objects with coordinates above a certain one go to the right subtree, all the rest to the left.

There may also be a calculation of the average value, for example, along the selected axis.
Or building a median. Or in any other way.


Figure 6. Another abstract tree of objects.

Collision Search

Collision search on two hierarchical structures, in turn, can also be implemented in different ways.

To check for the intersection of two objects, you just need to create a tree (BVH-tree) for each object, where the node defines its part of the object through some kind of bounding volume.

Next, you need to walk through the trees and compare the node from one tree with the nodes of another, so as to move only in the direction where there is an intersection of their bounding volumes.


Figure 7. Object matching recursion tree.

Illustrations and Information

1. Christer Ericson. Real-Time Collision Detection, Volume 1. - A triangle and a useful paragraph about polyhedrons.
2. Hamzah Asyrani Sulaiman and Abdullah Bade. Bounding Volume Hierarchies for Collision Detection. - An excavator, a bunny, and quite simply about collisions, hierarchies.
3. Johannes Mezger. Collision Handling in Dynamic Simulation Environments: Bounding Volume Hierarchies. - Tree and polyhedron intervals. Briefly and thesis about the main issues of hierarchical structures of limiting volumes.
4. Rolf Lakaemper. Game programming Introduction To Collision Detection - A title enticement and a masterpiece with men. A simple overview of collision detection.
5. An example of a simple implementation search for intersections or collisions using the BVH tree and discretely oriented polyhedra.