Vacuum Design Abstract: A Random Process Model
Good day to all. In the comments on the Waterfall and Agile post : and yet, where does the effect come from? wishes were expressed to simulate the progress of the projects. I must say right away that I don’t have enough for more than articles in the genre of “notes on napkins”, alas, but nevertheless, the subject is interesting and trial Wolfram Mathematica is available and can work with stochastic differential equations. For example:
d progress (t) = plan (t) * d t + risk (t) * d w t
In this short post, specific plan and risk will be substituted. I must say right away that there will be no special miracles.
plan (t) is the speed of progress over time,
risk (t) is a (negative) addition to speed, designed to reflect delays in completing tasks, the emergence of new tasks and generally all sorts of problems. Next, the risk will be equal to -riskconstant * plan (t), where the first factor, some value, is greater than zero and less than one.
progress (t) is actually a function that reflects the level of the project (the initial value is 0, we will be interested in the value 1, corresponding to one hundred percent).
And then, looking at the equation, we can say.
Based on the equation, an obvious conclusion, but in practice ... it happens that people don’t always think about it.
The most interesting is the average time when the process will exit more than one. To calculate this, you have to use the theory ( this one ).
Let's get down to business and do some small research. Four plan functions will be taken as a basis: constant speed, with linear growth, quadratic function and square root.
The table shows the screenshots (trial Wolfram Mathematics broke with export) of the results for riskconstant = 0.5 and the time to check completion = 1.
And what conclusions can be drawn here? Yes, you will not do much, except that the control without feedback (that is, without the participation of progress (t) on the right side of the equation) is doomed to have an average delay if there are risks. And yes. Wherever you push the growth progress within the project (well, that is, initially do not move the risks forward or backward), with a probability of 0.5 you will be in time on schedule (these 0.5 are not directly related to riskconstant = 0.5, in this case it is a coincidence).
CDF (for version 10.0) can be downloaded here .
PS You will find errors - write urgently until the trial is over :) In three weeks, the carriage will turn into a pumpkin.
PPS Regarding Rat. proposals - the same way: suddenly someone will advise the feedback equation which is specific, or something like that.
d progress (t) = plan (t) * d t + risk (t) * d w t
In this short post, specific plan and risk will be substituted. I must say right away that there will be no special miracles.
plan (t) is the speed of progress over time,
risk (t) is a (negative) addition to speed, designed to reflect delays in completing tasks, the emergence of new tasks and generally all sorts of problems. Next, the risk will be equal to -riskconstant * plan (t), where the first factor, some value, is greater than zero and less than one.
progress (t) is actually a function that reflects the level of the project (the initial value is 0, we will be interested in the value 1, corresponding to one hundred percent).
And then, looking at the equation, we can say.
| For the project to be completed at all, it is necessary that the risk of losing progress should not always be greater than the growth of progress! |
Based on the equation, an obvious conclusion, but in practice ... it happens that people don’t always think about it.
The most interesting is the average time when the process will exit more than one. To calculate this, you have to use the theory ( this one ).
Let's get down to business and do some small research. Four plan functions will be taken as a basis: constant speed, with linear growth, quadratic function and square root.
The table shows the screenshots (trial Wolfram Mathematics broke with export) of the results for riskconstant = 0.5 and the time to check completion = 1.
| Constant function | 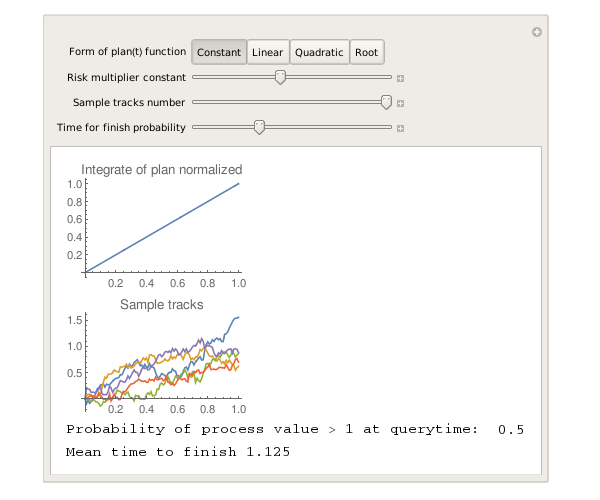 |
| Linear function |  |
| Quadratic function | 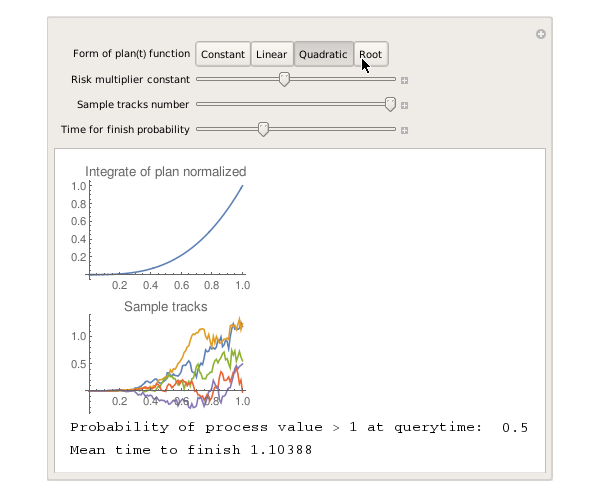 |
| Root function | 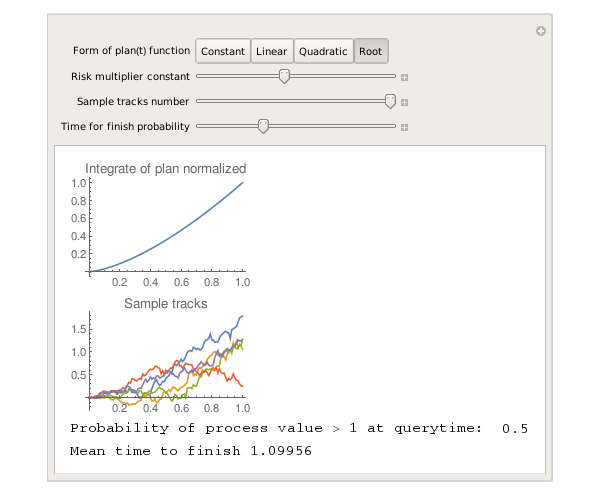 |
And what conclusions can be drawn here? Yes, you will not do much, except that the control without feedback (that is, without the participation of progress (t) on the right side of the equation) is doomed to have an average delay if there are risks. And yes. Wherever you push the growth progress within the project (well, that is, initially do not move the risks forward or backward), with a probability of 0.5 you will be in time on schedule (these 0.5 are not directly related to riskconstant = 0.5, in this case it is a coincidence).
CDF (for version 10.0) can be downloaded here .
PS You will find errors - write urgently until the trial is over :) In three weeks, the carriage will turn into a pumpkin.
PPS Regarding Rat. proposals - the same way: suddenly someone will advise the feedback equation which is specific, or something like that.
