Finding the simple on the complex: tips & tricks
I got a rather interesting projection here: find wire samples of standard sizes on roentgenograms of welds. It would seem that how much has already been written about the search for patterns in the image, standard approaches and techniques have been developed, but when it comes to real problems, academic methods are not as effective as expected. For starters, try to find all seven delays here:
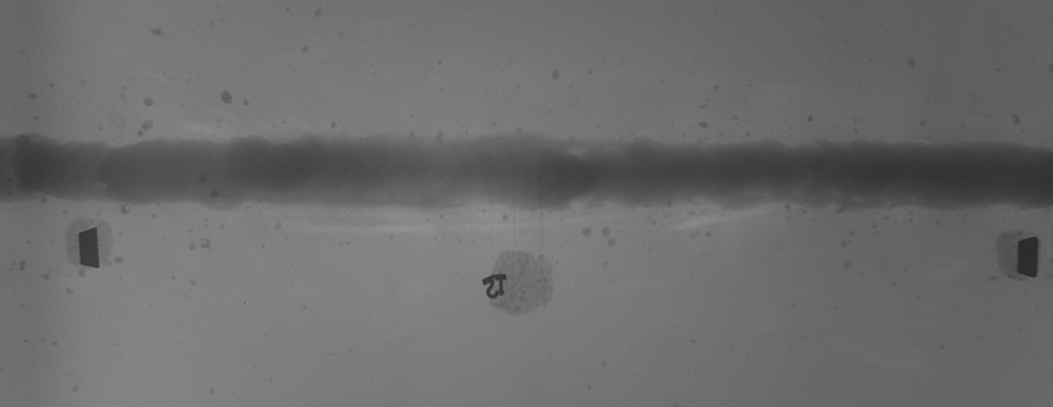
Actually, this is far from the easiest shot, but in the end even everything was found on it:

So, what are the conditions that were voiced to me:
- the files will be tiff and can be quite large - more 200 Mb
- images can be either positive or negative
- there can be several standards in one picture, you need to find everything
- the samples lie either almost vertically (+ -10 degrees) or almost horizontally
- there can be other standards and other elements on the frames
- the seams can be either straight or elliptical, horizontal and vertical
- the sample can lie on or near the seam
Maximum time to search for patterns in the picture:
- 3 seconds for a picture smaller than 100 MB
- 5 seconds for a picture larger than 100 MB and less than 200 MB
- 10 seconds, for a picture larger than 200 MB.
Also I have been given two types of standards GOST, which looks something like this:

That is, each standard consists of 7 wires of a certain length and a decreasing diameter located at given distances.
The lengths are different: 10, 20, 25, 50 mm.
For each length, there is a set of standards with different wire thicknesses, for example, one standard with a wire length of 25 mm has wire diameters of 3.2mm, 2.5mm, 2mm, 1.6mm, 1.25mm, 1.0mm, 0.8mm, 0.63mm, and the other 1.0 mm, 0.8mm, 0.63mm, 0.5mm, 0.4mm, 0.32mm, 0.25mm.
In total, there were about 16 standards in this way.
Thus, I had to localize fully deterministic objects in images of various quality.
I immediately thought about using trained classifiers, but I was confused by the fact that I had only 82 files with different standards, and thousands of images still need to be used for normal classifier training. So this path had to be taken away immediately.
The search for linear segments is well reflected in the literature.
The first thing that comes to mind is to search for segments by the Hough transform , but, firstly, it is very resource-intensive, and secondly, it will not be easier to search for weak signals among the stronger ones after the transformation. Even if you take a fairly successful crop:

it’s still quite difficult to find the delay:

(this is how it would look: ->
->  )
)
Another option would be to use loop filtering, but the problem arises: how to choose the binarization threshold in automatic mode?
Yes, and what to do with the contours, which mainly choose a weld or something else?
 ->
-> 


Loop detector with various levels of binarization.
The same applies to other loop detectors such as beamlets .
As it turned out, an extremely productive step was the simple calculation of the gradient map, i.e. just calculating the difference between two adjacent pixels. Such a step sharply highlights sharp edges and almost erases all slow transitions. Here's what, for example, happened after applying the gradients twice:
it was:

it became:

The contrast is increased in the bottom picture for clarity.
You must admit that even with the naked eye it has become much easier to find procrastination.
Immediately, another problem immediately became visible - noise. Moreover, the noise level is uneven in the picture.
How do we identify areas of interest for a more detailed study? Some method is needed that takes into account the local noise level and detects emissions significantly exceeding the average deviation.
Since the entire geometry of the standards is known to us in advance, we can choose the size of the window in which local statistics will be collected, thereby we can automate the choice of the binarization threshold. Not only that, since we know in advance that the wires will be approximately vertical, I decided to make an additional filter: if there are more significant emissions in the selected window than 1/2 of the vertical size of the window, then we select the entire vertical strip as an area of interest for further analysis ( Looking ahead, I’ll say that I also added an additional statistical detector for emissions that are several times higher than the standard deviation - it was necessary that all the letters and numbers on the frame also fall entirely into the area of further analysis and where they could be filtered out.
Here is what happened at this stage:

Here, blue, pink and black colors indicate the areas of interest obtained. Pink indicates the current cluster for which recognition is performed.
They dealt with pre-processing, it is necessary to proceed directly to the recognition of standards.
The first step here is clustering. It is necessary to somehow break up all the found points into clusters, so that later we can work with them.
Here the option came up pretty well just to add all the new points to the current cluster, if they are + -2 pixels vertically / horizontally.
In principle, this method can fail if the weld splits the wire into two spaced regions, so a second clustering option was provided when +15 vertical points were viewed.
Here, again, different options are possible.
Since the clusters have already been selected, one could take them and try to fit into the original picture the calculated versions of the standards with different angles, scales, shifts ... But as it turned out, this is again quite laborious and you can come up with a bicycle.
Namely: since we have almost vertical stripes, let's just make a projection along them, not even the original picture and not the gradient map, but the found clusters. This turned out to be enough to determine which standard in the image, if there are clusters corresponding to at least three wires.
In fact, I tried to project both the original image and the gradient map, but there was quite a lot of noise, and since we had already successfully fought with it while searching for clusters, you can simply use the results.
All this led to the following algorithm:
1. for each standard, we verify that the cluster length approximately corresponds to the length of the standard wires.
2. take a cluster, consider the projection along it + -100-150 pixels on the right and left, we will form a one-dimensional! array with peaks in the places of the found clusters.
The fact that the array is one-dimensional immediately gives us a gain in performance, plus we don’t need to look for angles (wires are parallel).
3. for several close scales (we know the scale only approximately), we calculate how a similar projection of each standard will look and do a convolution of the obtained projection of the standard and the projection along the cluster + we consider how many peaks there are in general in the projection along the cluster.
4. if there are other clusters on both sides of the cluster - we are in the middle of the standard, go to the next cluster
5. if nothing is found on both sides - we most likely stumbled upon a false cluster formed by “artifacts”
6. if nothing is on one side no, but on the other hand, there are less than two peaks - these are either artifacts or the wires are too thin, in any case we won’t be able to determine exactly where our standard is turned by only two wires
7. if on the one hand there are more than 2 peaks - we verify that the convolution with the reference projection makes a tangible contribution.
the convolution itself was considered like this:
where WSKernel is a reference projection, which has 1 in places where there is a wire and -1 where it is not (i.e., it looks like 1,1,1,1,1,1,1, -1, -1, -1, -1 , 1,1,1, ...)
ltrtr is the actual projection along the
tracemax cluster - this is the maximum intensity of the projection along the cluster.
All this works so that in places where there is a peak and it coincides with the standard, it gives a positive contribution (-k * tracemax needed to fine for not finding the wire in the right place, k = 0.1 turned out to be the most productive), and where it is, but does not match - negative.
After passing through several scales and standards, the maximum contribution is selected and it is believed that this cluster corresponds to this standard with a calculated scale factor.
Next - only the drawing and output of the results.
Well, a couple of examples:







Actually, this is far from the easiest shot, but in the end even everything was found on it:

So, what are the conditions that were voiced to me:
- the files will be tiff and can be quite large - more 200 Mb
- images can be either positive or negative
- there can be several standards in one picture, you need to find everything
- the samples lie either almost vertically (+ -10 degrees) or almost horizontally
- there can be other standards and other elements on the frames
- the seams can be either straight or elliptical, horizontal and vertical
- the sample can lie on or near the seam
Maximum time to search for patterns in the picture:
- 3 seconds for a picture smaller than 100 MB
- 5 seconds for a picture larger than 100 MB and less than 200 MB
- 10 seconds, for a picture larger than 200 MB.
Also I have been given two types of standards GOST, which looks something like this:

That is, each standard consists of 7 wires of a certain length and a decreasing diameter located at given distances.
The lengths are different: 10, 20, 25, 50 mm.
For each length, there is a set of standards with different wire thicknesses, for example, one standard with a wire length of 25 mm has wire diameters of 3.2mm, 2.5mm, 2mm, 1.6mm, 1.25mm, 1.0mm, 0.8mm, 0.63mm, and the other 1.0 mm, 0.8mm, 0.63mm, 0.5mm, 0.4mm, 0.32mm, 0.25mm.
In total, there were about 16 standards in this way.
Thus, I had to localize fully deterministic objects in images of various quality.
Path selection
I immediately thought about using trained classifiers, but I was confused by the fact that I had only 82 files with different standards, and thousands of images still need to be used for normal classifier training. So this path had to be taken away immediately.
The search for linear segments is well reflected in the literature.
The first thing that comes to mind is to search for segments by the Hough transform , but, firstly, it is very resource-intensive, and secondly, it will not be easier to search for weak signals among the stronger ones after the transformation. Even if you take a fairly successful crop:

it’s still quite difficult to find the delay:

(this is how it would look:
 ->
->  )
)Another option would be to use loop filtering, but the problem arises: how to choose the binarization threshold in automatic mode?
Yes, and what to do with the contours, which mainly choose a weld or something else?
 ->
-> 


Loop detector with various levels of binarization.
The same applies to other loop detectors such as beamlets .
What can be done to improve the situation?
As it turned out, an extremely productive step was the simple calculation of the gradient map, i.e. just calculating the difference between two adjacent pixels. Such a step sharply highlights sharp edges and almost erases all slow transitions. Here's what, for example, happened after applying the gradients twice:
it was:

it became:

The contrast is increased in the bottom picture for clarity.
You must admit that even with the naked eye it has become much easier to find procrastination.
Immediately, another problem immediately became visible - noise. Moreover, the noise level is uneven in the picture.
How do we identify areas of interest for a more detailed study? Some method is needed that takes into account the local noise level and detects emissions significantly exceeding the average deviation.
Since the entire geometry of the standards is known to us in advance, we can choose the size of the window in which local statistics will be collected, thereby we can automate the choice of the binarization threshold. Not only that, since we know in advance that the wires will be approximately vertical, I decided to make an additional filter: if there are more significant emissions in the selected window than 1/2 of the vertical size of the window, then we select the entire vertical strip as an area of interest for further analysis ( Looking ahead, I’ll say that I also added an additional statistical detector for emissions that are several times higher than the standard deviation - it was necessary that all the letters and numbers on the frame also fall entirely into the area of further analysis and where they could be filtered out.
Here is what happened at this stage:

Here, blue, pink and black colors indicate the areas of interest obtained. Pink indicates the current cluster for which recognition is performed.
They dealt with pre-processing, it is necessary to proceed directly to the recognition of standards.
The first step here is clustering. It is necessary to somehow break up all the found points into clusters, so that later we can work with them.
Here the option came up pretty well just to add all the new points to the current cluster, if they are + -2 pixels vertically / horizontally.
In principle, this method can fail if the weld splits the wire into two spaced regions, so a second clustering option was provided when +15 vertical points were viewed.
Pattern Recognition
Here, again, different options are possible.
Since the clusters have already been selected, one could take them and try to fit into the original picture the calculated versions of the standards with different angles, scales, shifts ... But as it turned out, this is again quite laborious and you can come up with a bicycle.
Namely: since we have almost vertical stripes, let's just make a projection along them, not even the original picture and not the gradient map, but the found clusters. This turned out to be enough to determine which standard in the image, if there are clusters corresponding to at least three wires.
In fact, I tried to project both the original image and the gradient map, but there was quite a lot of noise, and since we had already successfully fought with it while searching for clusters, you can simply use the results.
All this led to the following algorithm:
1. for each standard, we verify that the cluster length approximately corresponds to the length of the standard wires.
2. take a cluster, consider the projection along it + -100-150 pixels on the right and left, we will form a one-dimensional! array with peaks in the places of the found clusters.
The fact that the array is one-dimensional immediately gives us a gain in performance, plus we don’t need to look for angles (wires are parallel).
3. for several close scales (we know the scale only approximately), we calculate how a similar projection of each standard will look and do a convolution of the obtained projection of the standard and the projection along the cluster + we consider how many peaks there are in general in the projection along the cluster.
4. if there are other clusters on both sides of the cluster - we are in the middle of the standard, go to the next cluster
5. if nothing is found on both sides - we most likely stumbled upon a false cluster formed by “artifacts”
6. if nothing is on one side no, but on the other hand, there are less than two peaks - these are either artifacts or the wires are too thin, in any case we won’t be able to determine exactly where our standard is turned by only two wires
7. if on the one hand there are more than 2 peaks - we verify that the convolution with the reference projection makes a tangible contribution.
the convolution itself was considered like this:
if (WSKernel[i] == 1)
{ // punish more if there is no line:
convlft += WSKernel[i] * (ltrtr[lngth - i] - k * tracemax); //ltrtr is always positive as a sum of presences of clusters
convrgt += WSKernel[i] * (ltrtr[lngth + i] - k * tracemax);
}
else // WSKernel[[i]]==-1
{
convlft += WSKernel[i] * ltrtr[lngth - i];
convrgt += WSKernel[i] * ltrtr[lngth + i];
}
where WSKernel is a reference projection, which has 1 in places where there is a wire and -1 where it is not (i.e., it looks like 1,1,1,1,1,1,1, -1, -1, -1, -1 , 1,1,1, ...)
ltrtr is the actual projection along the
tracemax cluster - this is the maximum intensity of the projection along the cluster.
All this works so that in places where there is a peak and it coincides with the standard, it gives a positive contribution (-k * tracemax needed to fine for not finding the wire in the right place, k = 0.1 turned out to be the most productive), and where it is, but does not match - negative.
After passing through several scales and standards, the maximum contribution is selected and it is believed that this cluster corresponds to this standard with a calculated scale factor.
Next - only the drawing and output of the results.
Well, a couple of examples:






