Explaining the physical essence of the Wing Lift phenomenon without using the Bernoulli equation
Monin Ilya Alekseevich, Ph.D. CM-9, imoninpgd@gmail.com
Criticism of the existing Theoretical Explanation of Lift on the wing of an aircraft
After listening to the lectures of MIPT Faculty of Aeromechanics and Flying Technique (FALT) “Introduction to Aerodynamics” and reading several different university students on “Aerodynamics” [1-3], I was puzzled by a number of obvious contradictions in the explanations of the physics of the flow around air (gas or ideal). fluid) of various solid objects and the formation of lift on the wing.
For the flight of the modern aircraft necessary lifting power of 500-600kg / m.kv. When taking off and landing, the speed of modern aircraft is about 250km / h. In this case, the necessary lift force on the wing is ensured at a flow rate of the upper plane of the order of 450 km / h.
What is the mechanism for such acceleration of air flow without a visible mechanism for accelerating exposure to it?
After all, the contact of the wing with the oncoming flow can only lead to deceleration of the flow, but not to its acceleration!
These contradictions must be removed!
Physics should not lose physical meaning in favor of beautiful and complex mathematical constructions!
Let us consider a different explanation for the formation of wing lift without revealed violations of the laws of physics and common sense. This will require the application of the laws of ordinary mechanics.
In consideration, we consider that air consists of separate mutually repelling (for creating gas pressure) particles with their own mass, each of which obeys the laws of mechanics when its direction changes and the magnitude of the speed of movement changes.
The considered real wing is not an element of an ideal tube in the model of Bernoulli's Law, but is a bounded solid object in the unlimited space of a moving real gas consisting of completely tangible in mass and size of gas particles. In this case, one should consider the curvilinear flow of the jets over the curved surface of the wing, taking into account the inertia forces and the generated pressure, perpendicular to the velocity vector and the surface of the wing.
If we consider the motion of the jets above the wing profile, then a jet of air can create a vacuum over the wing due to the curvilinearity of its current.
So for the curvature of the rectilinear motion of the body it is necessary to apply a force in the direction perpendicular to the velocity vector. In the case of a continuous flat jet for its curvature it is necessary to ensure the difference in pressure above and below it. In this case, on the side of the convexity of the jet there will be an increased pressure, and on the concave side, a reduced pressure.
When moving along the circumference of the material point, the centripetal acceleration will be created by the force
F = m * V ^ 2 / R
And with the same circular movement of a thin layer of gas of thickness dR the mass will be equal to
m = q * S * dR ,
where S is the area of the gas layer portion, q is the gas density. If we bring the centripetal force to the elementary area of the gas layer, the force will turn into pressure
P = q * V ^ 2 * dR / R
When an air jet flows along the surface of the wing, the gas layer moves along a curved path. At each point of this trajectory there is a radius of curvature, which allows you to calculate the inertial gas pressure in a direction perpendicular to the velocity.
Thus, it is possible to directly calculate the pressure (vacuum) on the wing from the layer of gas flowing above its surface, while the gas flow velocity will always be considered equal to the flight velocity of the wing Vo.
To begin with, we consider the simplest case of a wing in the form of a plate of zero thickness bent with a radius R. Such thin curved profiles are used for ultra-light gliders in aircraft modeling.
By the way, according to the usual theory with the Bernoulli law, a thin curved plate should not have any lifting force at all, since the length of the path under the wing and above the wing is the same. But the lifting force of the thin wing is, moreover, very significant, which unequivocally shows the incorrectness of the lift model using the Bernoulli law.
For an estimate calculation of the wing, we choose the profile height that is usual for low-speed airplanes 20% of the wing width. In this case, for the height of the profile, we take the difference in the heights of the leading and trailing edges in relation to the horizontal air flow (see

fig. 1-3) . Geometry of a thin wing of constant curvature
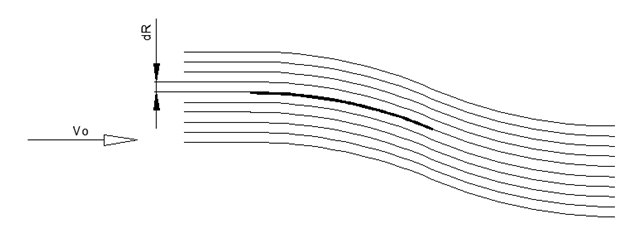
Fig.2. Estimated flow around a thin radius wing
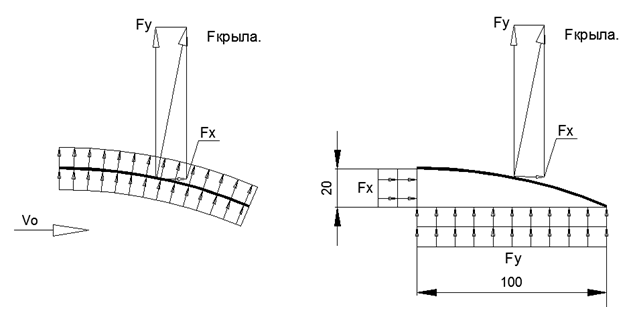
Fig.3. Character of pressure distribution along a thin radius wing and resultant forces in directions
Then with a width of 1 m and 20% of the profile height the wing radius will be 2.6 m, provided that the tangent to the wing is horizontal at the top of the profile.
Now let's calculate the centripetal pressure on the wing from the curved air layer along the arc.
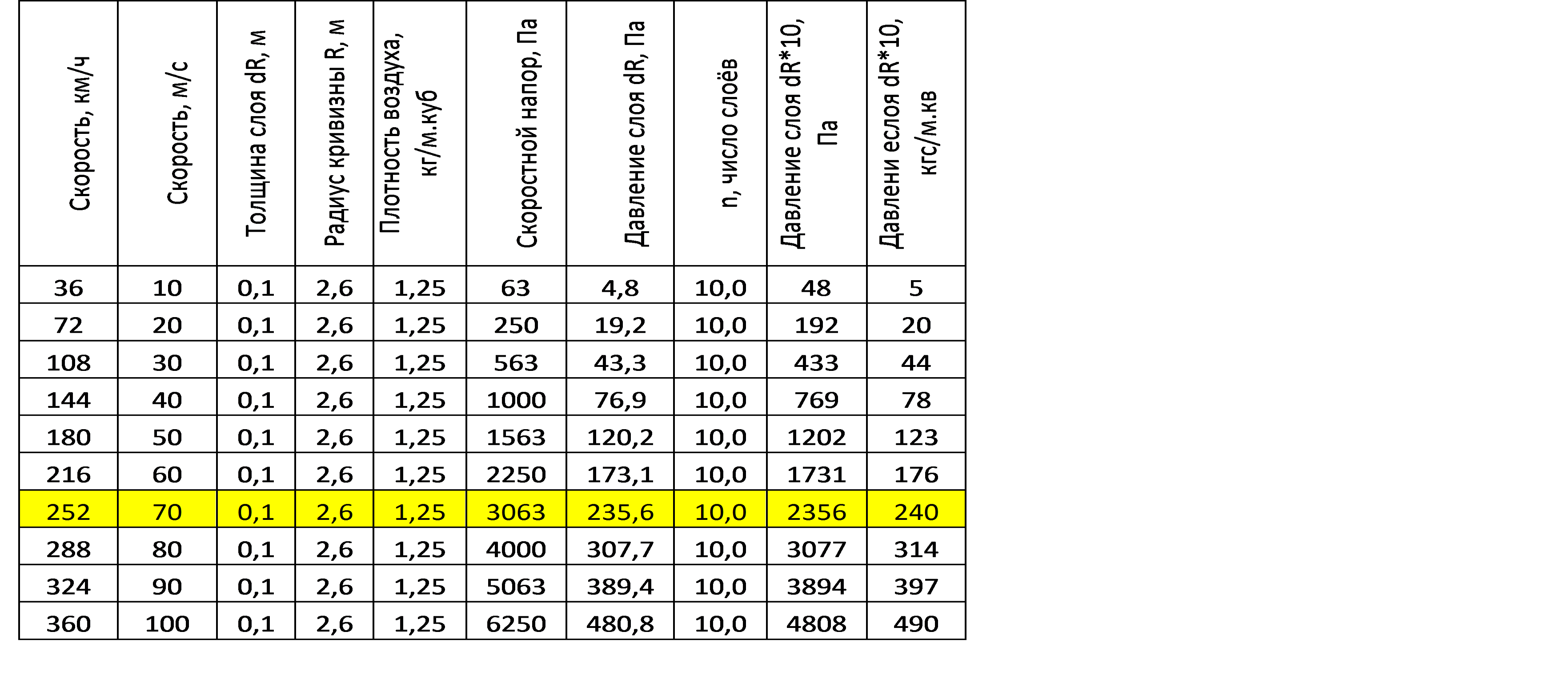
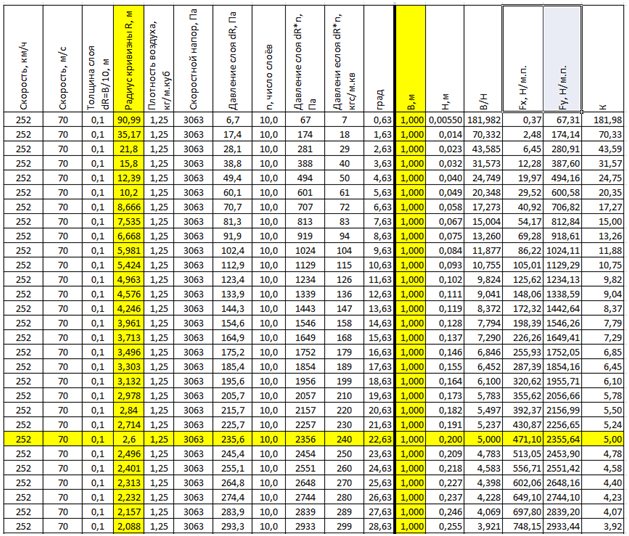
So, for a speed of 70 m / s (252 km / h), the pressure of a single layer 0.1 m thick with a radius of curvature of 2.6 m is 235.6 Pa or 24 kg / sq. M, and the value of velocity head at 70 m / s is 3063 Pa.
If we take into account that a thin wing has a flow around it from two sides, then these values need to be at least doubled, and then multiplied by a number of parallel layers, also bent by a moving wing. If we assume that the thickness of the perturbed layer is not less than half the width of the wing on each side of the wing, then we obtain a total redoubled load on the wing of about 2,356 Pa. These figures are perfectly beaten with the values of loads on the wing for low-speed light aircraft with a thick wing and a similar surface curvature of the wing. (see tab.1)
Since the pressure Pcr is applied to the curvilinear surface of the thin plate, the force Fcr from Pcr can be decomposed into Lifting force Fy and into force Resistance to flight Fx.
The lift force Fy is equal to the integral of the projection on the Y axis of forces from the Curvilinear flow pressure Rcr over the entire area of the wing.
In the case of uniform pressure on the pivoting wing, the value of Fy will be equal to the product of Pcr and the area of the projection of the wing to the X axis, which is equal to S = B * L of the wing (in this case, 1 sq. M.).
Fy = Pcr * Bcr = 2356 * 1 = 2356 N / m.
At the same time, the resistance to horizontal movement in this case will be equal to the integral of the projection dFcr on the X axis over the entire area of the wing. In the case of uniform pressure on the wing, the value of Fx will be equal to the product of Rcr and the area of the projection of the wing on the Y axis, which is equal to the height H of the wing profile (in this case, 0.2 square meters).
Fx = Pcr * Ncr = 2356 * 0.2 = 462 N / m.
At the same time, we obtain К = Fy / Fx = (Ркр * Bкр) / (Ркр * Нкр) = Bкр / Нкр, that is, with uniform pressure on the circular thin profile, the quality of the wing is equal to the ratio of only the geometric parameters of the profile К = В / Н.
According to the rule of vector decomposition of forces from a given picture, you can immediately get the value of the quality of the wing K = Fy / Fx, which in this case is equal to K = 100 * Pcr / 20 * Pcr = 5.
Interestingly, if you scale this design wing in the direction of a tenfold decrease (along the radius of curvature, height and width of the profile), then the pressure on the wing will remain unchanged at equal flight speeds (see table 2). It is for this reason that heavy cruise missiles fly on fairly small thin wings. It turns out that their small in size and thin wings with sufficient curvature is really enough to create the necessary lift!
Since room modeling is quite cheap, these numbers are rather simply checked on full-scale models.
Tab.1. The pressure of the curved air layers on the wing of constant radius R = 2.6 m, depending on the speed of flight.
Tab.2. The pressure of the curved air layers on the wing of a constant radius R = 0.26 m, depending on the speed of flight.

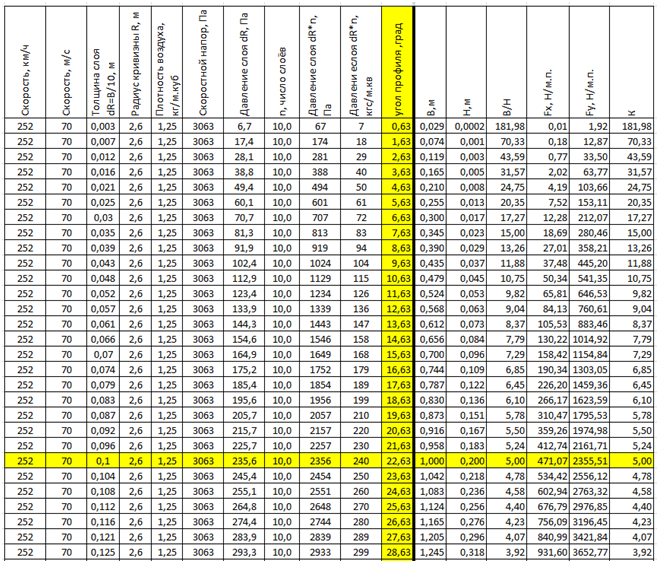
It is interesting to consider how the wing CRC changes with its constant curvature Rcr, but with the variable parameter of the Wcr profile width. (See tab.3)
In the very first line of the table, the aerodynamic quality of the wing reaches a fantastic value of K = 182, but the wing load is only 67 Pa (7kgs / sq.m), which is suitable only for room model gliders.
The required lift force on the wing arises only when the wing K is sufficiently small, as can be seen from the last lines of the table.
Yellow indicates the column of the variable parameter and the line of the original profile with CRC = 5.
Tab.3. Changes in wing parameters of constant radius R = 2.6 m at various profile angles (profile width) at a constant flight speed.
You can also calculate the change in lift force Fy and the wing quality Kkr for a wing with a constant chord, but different wing curvature at a constant speed. The yellow columns are: Variable argument Rcr - radius of curvature and constant width of the profile Wcr. Also highlighted line of the original profile with CRC = 5.
Tab.4. Changing the parameters of the wing of a variable radius of curvature at a constant width of the profile B = 1 m at a constant speed of flight.
In the described model, to obtain a vacuum above the wing does not require additional acceleration of air above the wing. A noticeable discharge above the wing is provided in conditions of a significant curvature of the air stream flowing around the wing under the action of static air pressure forces of the entire surrounding space. The angle of inclination of the chord of the original curved plate is 11.3 degrees (half the angle of the arc segment at 22.6 degrees), which is in good agreement with the landing modes of the wing of modern airliners when landing with the wing mechanization released (slats + flaps). In the landing mode, the wing with the released mechanization is much more like the case of a curved thin plate considered than the classical wing with a straight lower plane (see figure 4).

Fig.4. Wing asymmetric profile with a flat bottom streamlined surface: a) straightened position for high-speed flight; b) a wing with maximum curvature with fully released mechanization.
Strongly curved thin wing is widely used as fan blades. Low linear velocities at low pressures make it possible to use thin steel or plastic plates of extremely small thickness in the fans as blades, as their strength is sufficient to withstand the existing loads.
In heavy aircraft, the use of thin wings is technically impossible due to their insufficient strength. The large thickness of the wing allows you to place inside the wing sufficiently high load-bearing beams of sufficient strength and rigidity for bending and torsion, while maintaining an acceptable weight for the aircraft. It is for this reason that all the aerodynamics is studying the wings with quite tangible thickness. For this reason, we move from considering the aerodynamics of a thin curved plate to a wing profile with real thickness and planes of different curvature.
At the end of the consideration of the thin-wing flow model, it is necessary to present one more proof of the efficiency of the proposed model for explaining the “Wing lift”. As is known from mechanics, Force is the change in momentum per unit time, that is,
F = d (m * V) / dT
In the voiced model of a thin curvilinear wing flow, we can calculate lift force Fy as a change in the vertical air flow pulse, which is counted as
Fy2 = (dR * 10 * q * Vo) * Vo * sinAcr ,
Where Vo is the wing velocity, dR is the thickness an elementary curved layer of air flow in the design model; 10 is the number of simultaneously curved layers; Acr is the angle of the flow from the wing to the direction of the initial velocity Vo.
After carrying out the calculation we get that both calculations give the same result.
Or in analytical form:
Fy1 = Pcr * Bcr ,
Pcr = (dR * 10 * q * Vo) * Vo / R ,
Bcr = R * sinAc By
substituting the sweep Pcr and Bcr into the expression for Fy1 and reducing the like R in the numerator and denominator, we will receive:
Fy = Ркр * Bкр = (dR * 10 * q * Vo) * Vo * sinАкр
And it means that the equality is always true Fy = Fy1 = Fy2
That is, the “Inertial-curvilinear” method of calculating the “Lift Force” of the wing gives a formula that is identical with the method “Reactive “Impulse Force” for a wing of the same geometry.
This means that airplanes do not fly due to some kind of “magic” force from the “magic whirlwinds”, but due to the old and understandable “Impulse of Power” or “Reactive thrust” when the air mass is dropped down.
At low flight speeds during takeoff and landing (M = 0.2 or 250 km / h), the velocity head does not exceed 3 kPa (3% of the atmospheric pressure at sea level at 100 kPa), that is, it is so small in relation to the basic atmospheric pressure that Geometric compression of the flow becomes visually undetectable when drawing a jet stream at the wing.
To create a lift above the wing, it is necessary to create a curvature of the flow so that the wing is in the area of the concavity of the air flow. To ensure such a curvature of the jet above the wing helps the curvature of the upper plane of the wing, located in the aerodynamic shadow of the nose fairing.
In this case, the lower plane of the wing is flown either in a straight line without creating a vacuum, or over a concave surface, rejecting the flow of air downwards, which creates a positive increase in pressure on the wing from below and is summed up with the lifting force from the vacuum above the wing.
The main difference between a thick wing and a thin plate in our case will be the appearance of a frontal fairing, pushing the opposite air flow before it reaches the curved planes that create lift.
A braking zone occurs in front of the flying thick wing, where the velocity of the air becomes zero (relative to the wing), and the overpressure in this zone is equal to the velocity head Pvo.
Drawing current lines without taking into account air compression will not work, otherwise you will have to either accept the version of the acceleration of air above the surface of the wing, or the zone of influence with curvature of the flow will rush to infinity in an incompressible medium, which is implausible.
By the way, both effects (Acceleration of the flow and Infinite zone of influence in incompressible liquids) manifest themselves in practice in wind tunnels with smoke current lines and during the movement of submarines at shallow depths.
So in wind tunnels (ADT), the flow around the test mock-ups occurs with a noticeable acceleration of the flow (reduction of the thickness of the smoke lines) in the gap wall of the ADT layout. That's just the interpretation of this phenomenon is completely incorrectly attributed to the acceleration of the flow for the formation of lift. In fact, the acceleration of flow in the gap “wall ADT layout” is simply a consequence of narrowing the flow area in the flow path of the ADT while maintaining a constant air flow in the ADT itself due to powerful fans with a hard fan characteristic.
When submarines move at shallow depths above the submarine, a visually noticeable water hump forms. The size of this hump is equal to the volume of water in front of the hull of the submarine, which must somehow be moved from the area in front of the submarine to the stern when moving at a given speed. A hump on the surface is also formed when the submarine moves at great depths, but due to the larger spreading area of the hump, its height becomes undetectable with simple visual observation. The cause of the water hump on the surface is explained by the inability to move the incompressible fluid towards the bottom, and a thin layer of water under the atmospheric pressure of the air becomes Easily Shifted, with an understandable elastic characteristic of the Atmospheric pressure and Forces. By the way
Thus, we assume that the gas is compressible, and the zone of influence from the wing bending around is made dependent on the magnitude of the compression of the jet on the pressure Pvo.
The pressure in the stagnation zone at the fairing is maintained by curved air jets enveloping the fairing. The connection of pressure with the curvature of the layers of air is the same as in the case of a thin curved wing dP = q * Vo ^ 2 * dR / RSl.
The magnitude of the zone of influence, where the curvature of the flow is noticeable, is also related to the magnitude of Vcr and Ncr. An increase in pressure in front of the fairing will be compensated by a decrease in pressure in the wake behind the wing, that is, the wing forms a linear dipole in pressure, which at a great distance practically ceases to affect the surrounding air space at low (subsonic) flight speeds.
If you take the shape of a round nose cone, then half the profile height will be equal to Ncr / 2 = Rlob.
We consider that the stagnation zone with pressure Pvo is entirely created by the curvature of the layer within the width of the Vcr profile, then we can estimate the radius of curvature of the jet with a thickness of Ncr / 2 = Rlob.
It is necessary to fulfill the condition Pr = Рvo.
Therefore
qVo ^ 2 * Rlob / R = qVo ^ 2/2
After reducing the same terms of density and speed, respectively, in the left and right side of the equation we get
R = 2 * Rlob
Thus, it turns out that the limiting radii of the flow curvature are limited solely by the curvature of the fairing ( local profile height), and it does not depend on speed.
When turning the incident jet to bypass the profile, a situation inevitably arises in which the boundary jet with the zero flow line touches the fairing. At this touch point, the flow velocity is directed away from the wing, and the flow curve reaches the inflection point. That is, at this point, the separation of the layer from the wing occurs with a change in the direction of convexity of the curvature of the jet (see figure 5).
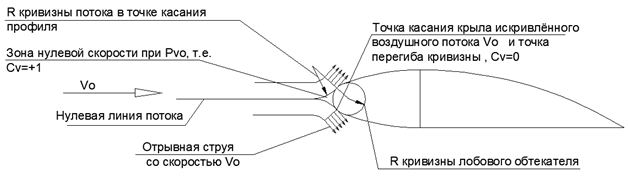
Fig.5. Interaction of the incident flow Vo with the front wing fairing.
At high flight speeds, the magnitude of the velocity head Pvo is so large that the jet breaks off from the nose fairing and, having described a long arc above the wing plane, returns back to the wing surface.
At the point of return of the torn off jet to the plane of the wing, an Impact occurs, and the jet abruptly changes direction to be tangent to the plane of the wing. In this case, under the arc of a flying jet from the separation point to the return point, a closed low-pressure cavity arises. (see figure 6).
In the traditional “Bernoulli Aerodynamics”, the described formation of a developed detachable bubble with a strong discharge and a shock return of the detachable jet is explained as follows: “... At high pre-sonic and transonic speeds, acceleration of air flow over the wing to supersonic values occurs, resulting in pressure over the wing being greatly reduced, and then there is a jump in pressure (the impact of the transition to supersonic), with the transition after it to a subsonic flow ... ". Such an explanation looks like an obvious stretch of real experimental data on an inconsistent theory.
Since the fairing divides the incident flow into two parts along the zero line, flow separation occurs on both planes of the wing. But due to the different directions of the planes with respect to the flow (to the flow or in the aerodynamic shadow), the tear-off discharge bubbles above and below the wing have a different size, and the impact force of the return jet changes in proportion to the size of the tear-off bubble.
On the basis of such a distribution, the pressure diagrams on the front wing fairing and the obtained CRC qualities of thin radius wing plates depending on the relative thickness of the Vrc / Ncr profile. It is easy to understand the causes and patterns of such a phenomenon as “streamlined” of various geometric shapes (see Figure Cx in Figure 6).
It would also be extremely interesting to consider the pressure diagrams for the flow around the standard axially symmetric bodies around the jet stream and obtain their cross-sections X and X along the sections, and not just one total coefficient X for the figure as a whole.
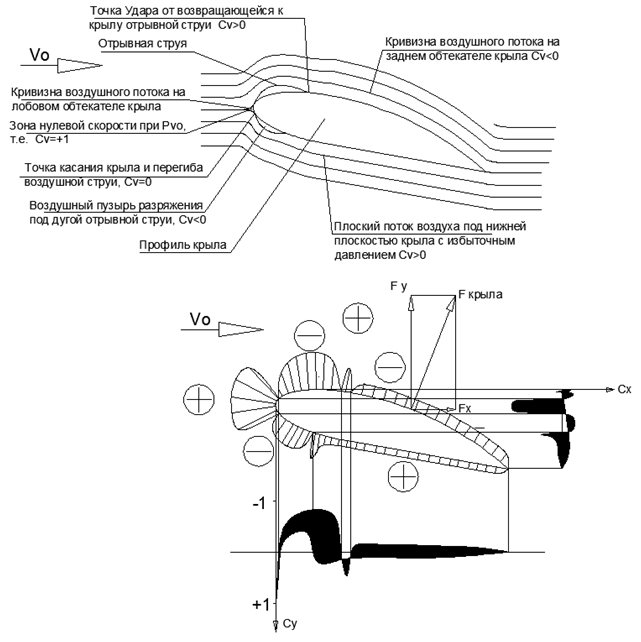
Fig.6. The flow of air around the thick wing with the designated characteristic elements of the movement. The diagram of pressures on the wing and diagrams of the pressure coefficient Su on the chord of the wing and Cx on the height of the wing. The area of the shaded zones corresponds to the total forces in the Y and X directions, respectively.
At low M numbers, the main lift force is formed in the zone of the nose fairing in tear-off bubbles. At low M numbers, the return jet in the separation zone goes tangentially to the thick profile of the wing and does not cause an Impact at the return point. But when approaching M = 1, tear-off bubbles inflate so much that it becomes impossible to achieve the desired profile thickness for a continuous flow of the jet, and then a pronounced separation of the flow occurs with the formation of a tear-off bubble visually observed from the vibrations of the silks glued to the wing plane. The expansion of tear-off bubbles in height becomes an obstacle to speeding, and therefore their development begins to decrease due to the sharpening of the nasal edge (lowering the radius of the frontal fairing).
At transonic flight speeds, the rear border of the detachable bubble reaches the trailing edge of the wing, after which the volumes of the upper tear-off bubble are connected to the high-pressure zone of the lower plane of the wing. In the combined volumes of the upper and lower tear-off bubbles, the pressure levels off, and the lift force of the wing Fy drops sharply.
During supersonic flight, the wing of the usual drop-shaped form becomes completely inapplicable, but instead a wing with a developed sharp “beak” appears, on which the main part of the lifting force is now created, with the possibility of a tear-off bubble being minimized.
To ensure the landing modes of flight at low Mach numbers in the “thin-beak” wing, the front and rear deflected mechanization are installed (see figure 7). This type of thin wings with sharp leading edges and deflected front and rear mechanization are put on combat fighters of 4-5 generations (see photo 1-2). When the mechanization deviates downward, the “thin-billed” wing becomes close to the flow characteristics of a thin curved plate, which allows taking off and landing at low speeds and with a short run on the runway. In the future, it is possible to switch to rotate the plane of the wing entirely when performing maneuvers at low speeds, as has already been done with the fully turning tail of fighters.
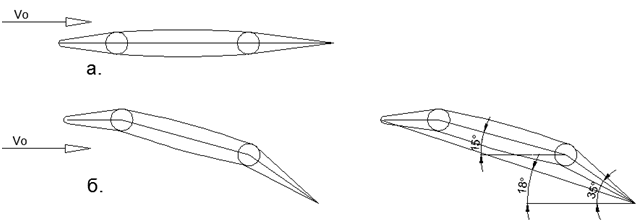
Fig.7. The thin-wing profile H / B = 0.1 (10%) with a sharp rejectable “Beak” and a wide flap that can be deflected: a) a straightened position for supersonic flight; b) the deviation of mechanization down for flying at low speeds and in landing mode with large angles of attack.

Photo.1. Su-35 at a large angle of attack with rejected slats and flaps in landing mode (landing gear released).

Photo.2. MiG-29 with deflected slats and flaps in take-off and landing mode at high angle of attack and low speed (landing gear released).

Photo.3. MiG-29 on takeoff with full deflection down the front and rear wing mechanization.
The photo (see photo 3) clearly shows the shape of the “sharp-billed” slat in cross section: a flat lower edge and a radial upper edge. The leading edge itself is not sharp, but has a very specific small radius, thereby improving the aerodynamics of subsonic flight. Controlling the inclination of the slat to the incident flow allows you to optimize the mode of formation of the tear-off bubble at low speeds, creating the conditions for its unseparated collapse. Also, given the aerobatic maneuvers with the possibility of a long flight upside down, the slant deflected upwards makes it possible to reverse the deflection of a flat thin wing for a completely effective flight in an inverted position, although with worse aerodynamics than in the normal position. On later Su-35 and Su-57 planes, the leading edge is sharper and more symmetrically wedge-shaped,
In the network, you can find a lot of explanatory material on any issue, including the Vortex formation on the wing of the aircraft, for example:

At the same time, it is easy to find photos of the vortex tracks from airplanes in the cloud layers that demonstrate a much larger scale of the phenomenon than they are trying to show this to us in theory

Photo.4. Vortex trail in the layer of fog for flying at a height of the plane. The rings of the visible fog vortex are hundreds of meters away from the aircraft, and visual proximity is an optical illusion created by a long-focus telephoto lens when shooting an airplane from a distance of several kilometers.

Photo.5. Vortex trail in the layer of fog for flying at a height of the plane. One can see the vertical air flow and the air waves approaching from the sides, spiraling in contact with the vertical downward flow.

Photo.6. Vortex trail in a layer of fog over the runway behind the landing plane.
These huge satellite vortices behind the planes are not formed at all at the expense of end vortices on the wing. Trailing vortices exist, of course, but their role is not so great, and aircraft designers are actively and successfully fighting it.
Large-scale eddies from photos are already forming far behind the plane, when the air wave thrown by the plane down is replaced from two sides by the flow of air from under the descending layer into the rarefied space from above (see photo 4-5). This explanation of the formation of a cocurrent vortex echoes the already considered issue of the “zone of influence of the wing on the surrounding space”. At the same time, the role of the earth’s surface lies in the boundary of the downward flow of air thrown down by the wing. That is, the flight of the aircraft and the creation of a “wing lift” is possible even in the absence of solid underlying surfaces, but at the same time the air stream thrown down will move infinitely long downward, losing speed and kinetic energy with distance, but keeping the vertical impulse unchanged. The kinetic energy of the original rejected air mass will be lost to the involvement in the movement of lateral air flows, the symmetrical multidirection of which will not change the initial total impulse created by the aircraft wing. A vivid illustration of the role of the Earth-Restrictor is Photo.6. There, the straight-line current of fog above the landing Airbus (see photo 6) descends to the ground in a straight line and only then far behind the plane begins a shift to the sides along the limiter-ground, and the layers of fog from the sides and from above already approach the middle of the cobweb, twisting in dual self-compensating spiral downward flow. A vivid illustration of the role of the Earth-Restrictor is Photo.6. There, the straight-line current of fog above the landing Airbus (see photo 6) descends to the ground in a straight line and only then far behind the plane begins a shift to the sides along the limiter-ground, and the layers of fog from the sides and from above already approach the middle of the cobweb, twisting in dual self-compensating spiral downward flow. A vivid illustration of the role of the Earth-Restrictor is Photo.6. There, the straight-line current of fog above the landing Airbus (see photo 6) descends to the ground in a straight line and only then far behind the plane begins a shift to the sides along the limiter-ground, and the layers of fog from the sides and from above already approach the middle of the cobweb, twisting in dual self-compensating spiral downward flow.
In the light of the stated role of the Earth in the formation of the “Lift Force of the Wing”, it makes sense to additionally consider the “Screen Effect”, which cannot exist without the presence of a solid earth surface. Thus, the physics of the Flight of the wing in the Endless airspace and on the “Screen Effect” near the Earth has a very different nature.
The effect of the close-lying surface of the earth on the wing lift is called the “screen effect”. With this effect, the lifting force of the wing increases dramatically when flying near a solid surface (ground, water) at a height comparable to that of the wing chord. Based on this effect, even a whole class of low-flying "Ekranoplans" appeared.
What is the essence of the phenomenon? Deal with this issue can only be assuming that the air is a compressible gas.
Then, when the wing is flying over the surface of the earth, an air gap of limited size is formed between two solid surfaces. When flying a wing with a small positive angle of attack, the counter-flow of air under the wing experiences a gradual compression from the leading edge of the wing to the trailing edge (see figure 8).
The maximum pressure of the compression on the flow screen under the wing depends only on the velocity head relative to the flying wing, and this pressure in the compressed layer cannot exceed the pressure of the velocity head of air:
Po = Vo ^ 2 * Q / 2 ,
where Rope velocity of air at wing speed Vо, Vо-flight speed of the wing, Q-density of air.
Knowing the maximum pressure increment under the wing, we calculate the geometrical parameters in the airbag gap.
So at a speed of 40 m / s (144 km / h), the velocity head Ro = 1kPa or 1% of 1 atm. (100kPa).
That is, at a speed of 40 m / s, the maximum pressure under the wing is achieved with compression of 1% over the height X of the gap from the leading edge of the wing to the rear. Such preload is almost undetectable to the eye, and the layer under the wing visually appears flat (see figure 8.a).
The angle of attack will be A = (Ro / Ratm) * X / B radians (at small angles sinA = A),
where B is the wing chord, X is the air gap to the ground below the wing at the trailing edge of the wing, Ro-speed air pressure at wing speed Vо, Ratm - atmospheric pressure (at sea level Ratm = 100 kPa).
It turns out that the maximum effective angle of attack for obtaining a screen effect depends on the height of the flight of the wing above the surface, the structural width of the wing and a given flight speed, and the angle of attack is only a derivative of these quantities.
Conclusion: It is possible to increase the width of the wing almost infinitely, reducing the angle of attack to almost zero, thereby achieving the minimum resistance Cx with the inductive component of resistance almost zero.
The “screen effect” at low flight speeds provides a very high wing quality, as it creates the maximum specific lifting force on the wing, equal to the velocity head Po at extremely low angles of attack on a practically flat and very thin wing. The quality of the wing at low Mach numbers when flying on the screen can reach a value of K = 25-30.
The contribution of rarefaction above the upper convex surface of the wing during such a flight on a “screen” with a flat wing is sufficiently small compared to the pressure under the wing.
When the flight speed increases, the velocity head grows quadratically, and to obtain the maximum screen effect, it is necessary to raise the angle of attack in proportion to the velocity head Po growth.
That is, increasing the speed of Vo in order to increase P entails an increase in speed of the Attack Angle that is quadratic in speed, which in turn dramatically reduces the quality of the wing. And starting with a certain speed Vo-max, the magnitude of the screen effect with a large angle of attack is compared with the lift of a conventional airliner in a landing mode with extended wing mechanization.
For any wing with a chord B to increase the height of flight X, it is necessary to lift the angle of attack, after which the Ekranoplan rises to some new height X2, where the balance of the degree of preload of the jet is again established due to the new angle of attack at the new height. At the same time, with increasing altitude, the flight of a ground-effect vehicle begins to linearly increase the resistance to flight and the corresponding thrust force corresponding to it also increases without changing the flight speed. That is, the fuel efficiency of the flight of an airplane can drastically change from a rise in height of only a few meters. For example, the maximum flight range of the Oriole ecologolet at a height of 0.8 m is 1,150 km, and at an altitude of 0.3 meters with the same load - already 1,480 km.
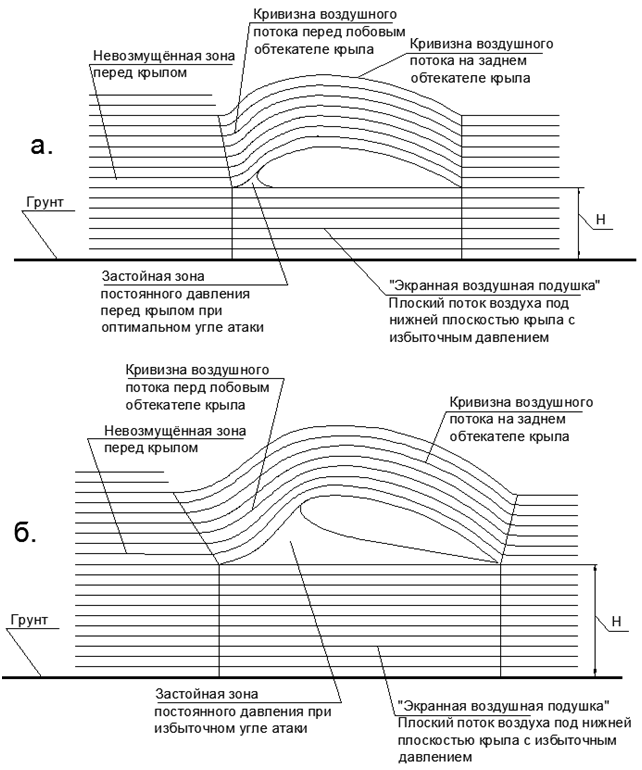
Fig.8. Airflow configurations on the “Screen Effect”: a.) Optimal angle of attack without a stagnant zone under the wing, b.) Excessive angle of attack, forming a large bubble of stagnant high-pressure air between the wing and the pre-loaded air layer of the “Screen Airbag”.
Conclusion: Additional tearing up of the angle of attack of the wing without increasing the flight speed on the screen does not increase the lift force, but only increases the flight resistance of Cx (see figure 8.b)
Considering the angle of the airliner’s chord in the landing mode about 15 degrees we can estimate the amount of jet compression under the wing to the pressure Ро and the corresponding speed Vо, considering the value of the chord B to be equal to the height of the flight of the wing X.
15 degrees corresponds to sin15 = 0.262
At an angle of attack of 15 degrees, there should be a speed head Ro = 0.26 atm = 26 kPa, but such pressures are realized at very high speeds (740 km / h) and far exceed the calculated wing loads required for flight. That is, such a large landing angle of attack to create a screen effect over the runway is excessive at landing speeds of 250-300 km / h.
The quality of the wing at an angle of attack of 15 degrees will drop to the value of just K = 3.7.
The landing speed of the airliner is only about 250 km / h (70m / s), while the velocity head will be Ro = 3kPa or only 3% of Rathm, while the design load on the wing in flight is normal to 5kPa (500kg / m.kv = 5% of Ratm). That is, when landing, the screen effect of an airliner begins to be noticeably felt by the pilot at a height comparable with the width of the wing B, comparable to the height of the landing gear. Leveling the aircraft and reducing the angle of attack for a speed of 250 km / h allows the aircraft to penetrate the “screen airbag”, since its carrying capacity is lower than the required pressure under the wing for flight.
Due to the “Screen Effect”, there is an “incompatibility” on an airplane in horizontal flight without releasing wing mechanization at an attack angle of 5% (or 3 degrees) with a speed head Ro = 5 kPa, which corresponds to Vo = 324km / h or 90m / s.
The angle of attack of 5% (or 3 degrees.) Creates the quality of the winged wig equal to K = 20.
High K = 30 corresponds to an angle of attack of 3% (2 degrees), while the support under the wing will be only 3% * Ratm = 3 kPa (300kg / sq.m), which corresponds to the velocity head at Vo = 70m / s (250 km / h)
Thus, cost-effective flight modes in the mode of "WIG" in comparison with the usual high-altitude "plane" lie in the zone of low speeds. When the wing wing quality drops below K = 20, it is more profitable to use ordinary high-altitude aircraft for transportation. That is, the cost-effective areas of operation of Ekranoplan correspond to speeds below 300km / h.
Separate consideration deserves the question of maneuvering Ekranoplan in flight. Since the wing lifting force on the “screen” is formed differently than during high-altitude flight, it cannot maneuver the “in-flight” ekranoplan.
An ekranoplan cannot lay bends with a roll on the wing, as it will immediately receive a loss of lift on the raised wing and touching the water with the wing lowered. For ekranoplan, rotation is possible only with a “pancake”, that is, completely without a roll, but only due to the creation of lateral forces from the vertical tail.
The vertical tail of the Ekranoplan itself should also be different from the aircraft tail. The Ekranoplan vertical tail should consist of at least two keels, capable of working both synchronously and separately, depending on the type of maneuver being performed. At the same time, the vertical tail unit not only turns the Ekranoplan around its vertical axis, but also creates a horizontal force across the direction of flight speed.
The horizontal tail fin on the rear keel adjusts to the angle of attack.
The wide and short wing must be equipped with developed end-washers, skegs, which keep the flow pressed under the wing from spreading to the sides. Additionally, these skeg washers serve as landing pontoons for landing.
You also need additional horizontal tail at the ends of the main wing to compensate for the overturning moment from the action of the vertical tail.
Practically according to this Scheme, the Bartini VVA-14 ekranoplan was built (see figure 9) and numerous versions of the EKP-airplane perspective layouts, where the side-tail washers play the role of the front vertical tail (see figure 10).
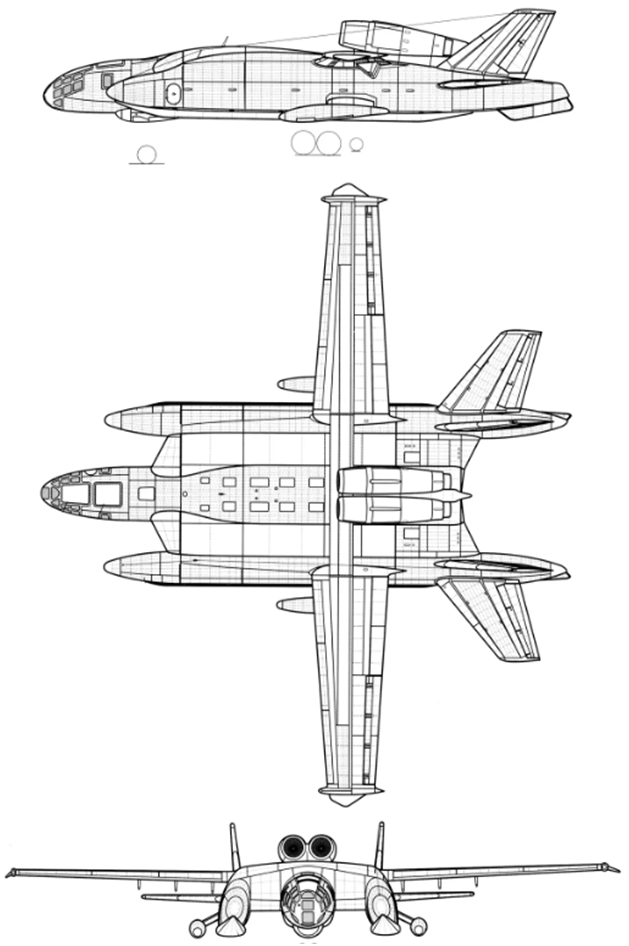
but.

b.

at.
Fig.9 Ekranoplan Bartini VVA-14. A. Drawing. b. Model in 3-D. at. Photo of the current sample on the water.

Fig.10. Layout of a promising large wig.
Types of maneuvers wig due to the vertical tail:
All these modes are practically little realizable in manual mode, since the low altitude simply leaves no time for reaction in the pace of human perception. To control the ekranoplan, automation control is needed, similar to the automatic stabilization of ultra-unstable 4-5 generation fighters.
All the above assumptions are based on openly published experimental data (pressure drop diagrams on the wing and other data obtained on ADT).
For experimental Aerodynamics for the last century, huge sums of money were invested in building ADTs of various types and sizes, as well as a huge amount of factual material was obtained in experiments with models of various aircraft and individual wing elements.
It is surprising that in the process of teaching students rely not on the materials of actual Experiments, but on dubious theories 100 years ago. And this is despite the fact that the experimental data themselves clearly contradict these mossy Theories.
Even in such a generalized introductory course as “Introduction to Aerodynamics” for PhALT Phystech, qualitative explanatory models of the basic concept of “Wing Lifting Force” are not given, but superseded by abstruse science-like juggling with mathematical formulas (which also do not allow to calculate anything).
In science, there has been a trend towards a split between theory and practical engineering application in the development of specific products. Explicit contradictions in the theoretical models are not advertised, but on the contrary they are silently silenced in order not to shake the authority of mossy and already deceased elders from the Academy of Sciences and not to interrupt the triumphant march of their sincere delusions through the pages of quite modern textbooks and monographs.
Ilya Alekseevich Monin, Ph.D., imoninpgd@gmail.com
In order to understand the development of “aviation” as an industry and “aerodynamics” as a science, you need to remember that first appeared the first aircraft built by on-the-spot engineers (see fig.11), and only then theorists began to emerge who created the discipline “Aerodynamics” based on the results of the creation of design engineers.
In the picture is a plane created by motorist Henri Farman, a remake of a purchased small-scale Voisen plane. At the same time, the original aircraft of the Vuazen brothers began to be produced only in 1907. At the time of purchase by Farman, the airplanes of Voisin could only jump slightly and jump several dozen meters. Farman, after a series of alterations of the original aircraft, made it possible to fly more than 1000m, while still turning around and, making a circle, land. There was a record flight Farman January 13, 1908. And in 1909, the Farman Brothers firm opened its own production of airplanes of its own design and a flight school for teaching the art of flying on them (see figure 12). The flight speed of the Farman aircraft was then about 60 km / h, which was shown in a record flight at a distance of 180 km, overcome in 3 hours of flight.

Fig.11. Layout of the aircraft Vuazen, converted to a record flight Farman in 1907-1908gg.


Fig.12. Layout of the aircraft "Farman IV-1910." In the museum, and a photo of the original sample at the airport.
It is clear that the first early aircraft were thin, light and low-speed.
These are the parameters that correspond to the first convex-concave thin profiles, more similar to the simplest curved sheet of plywood, and not to a complex profile with a deep theoretical miscalculation.
For reference, I give an illustration of the transformation of wing profiles from the earliest beginning of the 20th century, to the fully developed aircraft industry of the mid-40s. (see

figure 13) Fig.13. Trends in the profile of the wing of the aircraft of the first half of the 20th century.
After the first light experimental aircraft was followed by a rapid increase in the size and mass of aircraft for the transport of ever-increasing payload. Thin wings could not withstand such a scale and weight, which required installing high strong beams inside the wing, and making the wing itself flat-convex or even double-convex to hide the supporting beam behind the streamlined wing sheathing.
Already in the 20s, all wing profiles took quite a modern look.
By the 1940s, the aviation industry had developed so much that it began to produce whole armada of airplanes capable of carrying entire cities into the dust of the air. But with such an explosive development of production capacity, the theoretical base remained extremely weak.
By the 1930s, the intensity of aviation development did not allow building new airplanes according to the “intuition”, but required the construction of a powerful experimental base for blowing parts of airplanes, large-scale mock-ups and airplanes entirely on the ground in huge wind tunnels (ADT).
So in TsAGI in 1939, the largest at that time (the second in the world now) wind tunnel T-101 was launched, which allowed to explore on the ground entirely on actual flight speeds at that time.
Flow rate 5–52 m / s
Number of Re per 1 m to 3.6 ∙ 106
Total atmospheric pressure
Speed head up to 1.7 kPa
Ambient deceleration temperature
Angle of attack range (α) ± 20 °
Slip angle range (β) ± 180 °
Dimensions of the working part :
Nozzle section (ellipse) 24x14 m
Working part length 24 m
Sizes of test objects:
Wingspan: up to 18 m
Fuselage length: up to 30 m
Wing area: up to 35 m2
Since then, the airplanes have become much larger, and the flight speeds are much faster, so that not a single modern aircraft fits into the T-101 ADT entirely, and in more modern and more high-speed ADTs, they only blow large-scale dummies or structural elements separately.
True, in theory, since the beginning of the last century, little has changed, so that already at the end of the twentieth century, aircraft designers began to reinvent what designers in the early to mid-20th century had passed, but theorists did not explain. For example, let me give a view of the profile of the wing of the aerobatic plane, which was considered the best in the 1980s (see figure 14).

Fig.14. One of the wing profiles from the Aviation Profiles catalog.
The same recurring course of thought is observed among large samples of flight technology, this was reflected in the creation of WIG monsters in the 1960s and 80s (Fig. 15), little distinguishable from the giant planes of the late 1930s (Fig. 16).
At the same time, the screen effect itself was discovered as early as the beginning of the 30s at the time of landing large multi-engine aircraft with a large wing chord.
The same screen effect clearly manifested itself when landing a record long-distance ANT-25 aircraft, when during a test flight in 1933, the plane simply could not land, and with a light touch of the wheels of the ground, the plane jumped up and took off again. In order to remove this effect and ensure a smooth landing, it was even necessary to install special retractable brake flaps, which sharply worsen the flight performance of the wing during landing.
The wing chord in the widest root part of the ANT-25 exceeded the height of the landing gear, thus creating ideal conditions for the formation of a screen effect under a wide low-flying wing. Moreover, during landing with empty tanks with an aircraft mass of 4000 kg and a wing area of 88 square meters, the average load on the wing in flight was less than 50 kg / square meter, which corresponds to the velocity head 500 Pa created at a speed of 104 km / h (29 m / s) for flying on the screen. It is worth noting that the aircraft of that time flew extremely slowly (by modern standards), so the record ANT-25 had a cruising speed of about 165 km / h (max. 266 km / h at altitude), with a flight range of 10-12 thousand km and a duration of 75- 80 hours in a row.
A.
B.
C.
Figure 15. The ekranoplan "Caspian Monster": a.) In flight. B.) Stationary on the water full face. c.) Motionless in frontal projection.
A.
B.

Fig.16. Giant ANT-20 "Maxim Gorky", 1939. a) Sketchy section. B) Photos at the airport and during landing.
Often there are cases. When it is necessary to build airflow lines around bodies, the shape of which is difficult to call streamlined.
It is clear that the air will not obediently wrap around all the corners and notches of the body, but will go in soft twists, sweeping over the pits and filling them with vortexes of detached streams of stagnant zones.
If we consider the presence of stagnation zones as additional solid volumes of the profile itself, then the flow around the aerodynamic elements known to us will take a completely different form.
Interestingly, this method of finding the equivalent conditional prototype wing is used in existing applied Aerodynamics. In any case, the method of constructing a “Fictitious semi-infinite body” around a rigid wing is described in the textbook [3] for three whole pages (pp. 435-437), while choosing the border of the fictitious wing as the boundaries of the thick hindered boundary layer, that is, adding to the wing our very stagnant zones in the "tear-off bubbles" or turbulent zones with a complete disruption of the flow above the wing. The pressure on the solid wing from the high-speed air flow is considered to be equal to the pressure of this flow on the “fictitious body”. It turns out that the pressure is transferred from the speed jet to the solid wing through a sufficiently thick layer of slow-moving air of the boundary inhibited layer (stagnant zone) without any distortion.
Let us consider in detail the process of soft flow around high-speed jets of varying intensity of wing profiles and select various “stagnant zones”.
The case of full sticking of the flow to the wing at small angles of attack does not add any specialty (see figure 17), but a small stagnant zone appears on the front fairing, resembling a small sharp beak on a round bird head.
The element seems small, but it is extremely important to understand the phenomenon of “flow” in general.
Consider the usual profile of a wing in horizontal flight with pronounced tear-off jets, first with a zero angle of attack (see figure 18), and then the same wing is already at a large angle of attack (see figure 20).

Fig.17. The profile of the wing with a flow without breaks on the planes of the wing, but with a small zone of complete deceleration of the flow on the nose of the wing.
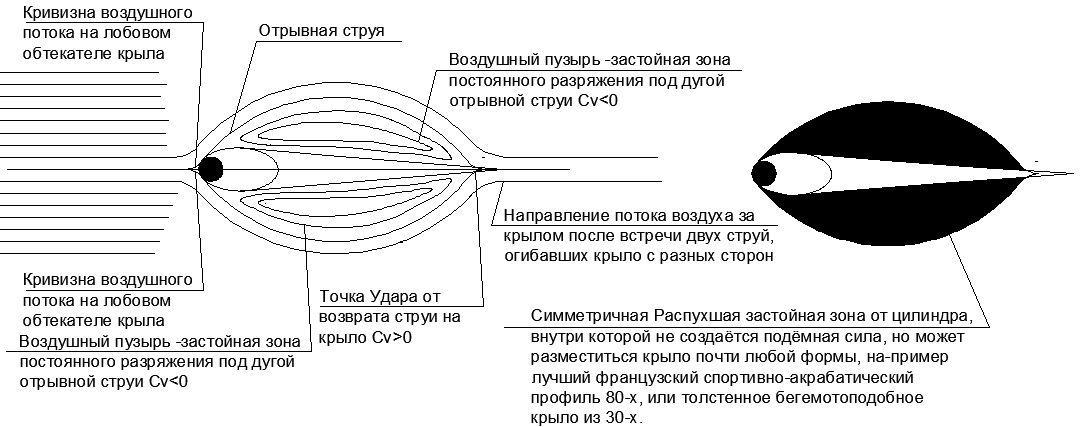
Fig.18. The profile of the wing with the separation of flows on the planes of the wing at zero angle of attack and its "Fictitious body".
Looking at a strong increase in the “Fictitious body” in comparison with the original pushing front fairing, it becomes clear how surprisingly low frontal resistance is obtained in long spindly bodies, for example, in aircraft fuselage.
The streamlining of such forms reaches Cx = 0.06, whereas for a ball of the same section Cx = 0.4..0.5, and for a flat plate Cx = 1.
It turns out that in the discharge under the detachable jets in the frontal projection, resistance is not created at all. It remains only to land a detachable jet on a straight surface parallel to the velocity vector so that the impact does not produce a longitudinal to velocity component. With such a task perfectly cope long cylindrical fuselage with an elongated ovoid front fairing. It turns out that the frontal resistance of a huge fuselage is equal to the resistance of the ball at the tip of the tapering nose (see figure 19.)
The ratio of the diameter of the ball in the nose cone to the diameter of the fuselage depends on the speed of flight, and the higher the speed of flight, the narrower the nasal rounding becomes, pushing airflow apart. The increasing energy of the oncoming flow with a constant amount of frontal section requires scattering less and less air to the side of the fuselage while maintaining a constant section of the “fictitious body” behind the fairing. In supersonic, the radius of curvature of the nose fairing degenerates into the tip, but this is a completely different story.
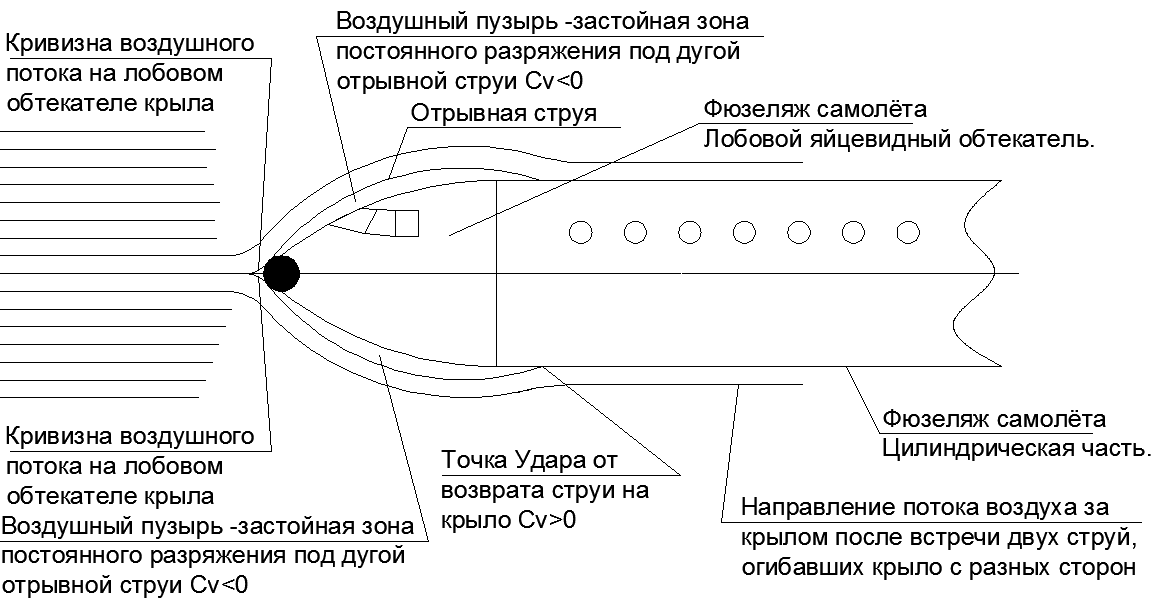
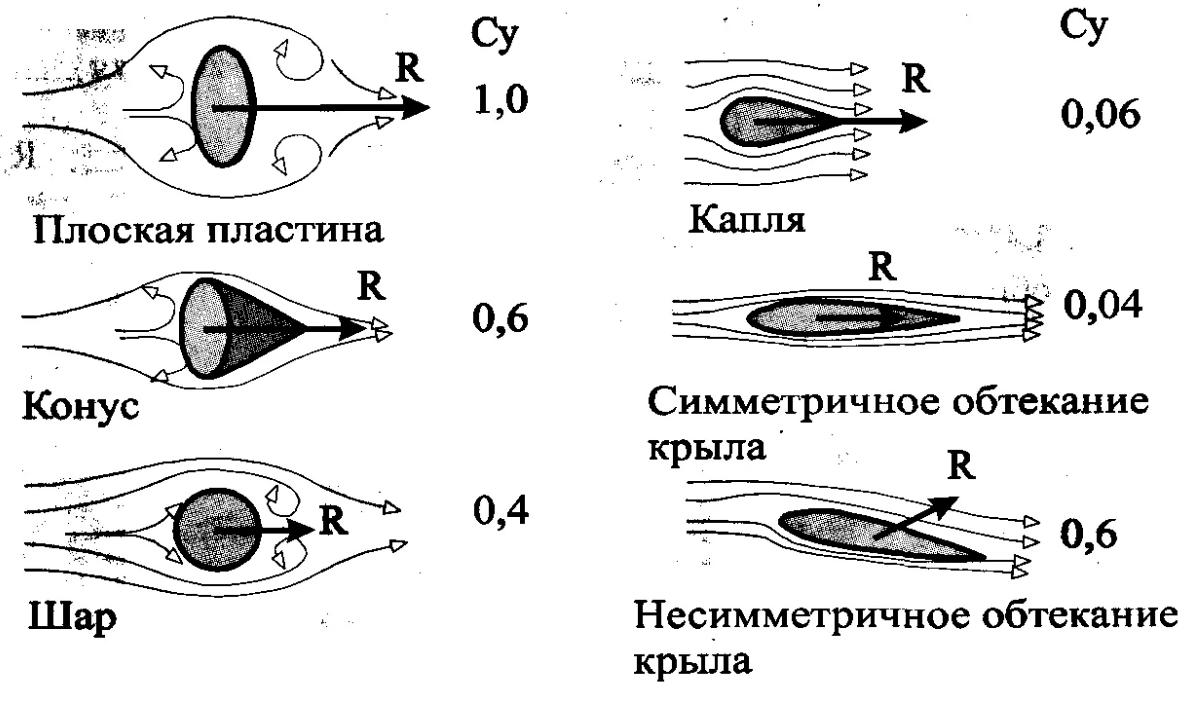

Fig. 19. Wrap around the fuselage with detachable jets, under which creates a zone of zero resistance to flight. All the resistance of the fuselage is equal to the aerodynamic resistance of the ball in its nose fairing. And accompanying illustrations from textbooks on the topic of comparing resistance when air flows around various bodies.
Now consider the behavior of the detachable turbulent zones with a wing with a large angle of attack (see Figure 20).
First, it is necessary to trace the trajectory of the detachable flow above the stagnant zone until it meets with the flow from under the wing of the aircraft. Since the profile of the frontal fairing of the wing is considered symmetrical cylindrical, the detachable jets have equal power and trajectory, that is, they are also symmetric.
For the horizontal wing, we have already received a symmetrical two-sided separation bubble with the closure of jets on the wing in the same places.
When giving the wing a large angle of attack, the pattern of tear-off jets changes. At the same time, the dimensions of the “Separated bubbles” = “Stagnant zones” above and below the wing begin to differ dramatically in terms of volume.
As a result, as a “fictitious body,” a very swollen wing will be obtained with a significant flattening of the lower plane compared to the huge dome of the tear-off bubble on the upper wing plane. Interestingly, the equivalent virtual profile of the “fictitious body” at a large angle of attack of the wing with bloated detachable bubbles on the upper plane of the wing is surprisingly similar to the well-known EKIP aircraft. (see figure 21 )

Figure 20. The profile of the wing with the separation of flows on the planes of the wing at a high angle of attack and its "Fictitious body".



Fig.21. Ekranoplan EKIP. The layout of the perspective model of the Ekranoplan and the existing umenshchennaya model of the Ekranoplan (never taken off because of the project shutdown).
That is, in the EKIP Ekranolet, quite a sensible idea was offered to control the stagnant zone in the rear "shadow" part of the hull, which allowed the detachment jet to settle on the wing in the upper part of the dome, which gives greater lift force and reduces aerodynamic resistance to flight.
It turns out that the author of the EKIP was not such an inventor, offering such a hippo-like structure as an aircraft.
True, the EKIP should not fly very fast and at high angles of attack of the initial thin profile (about 15 degrees), with a correspondingly high frontal resistance.
The huge volume of cargo space in such a flying wing can more than compensate for some deterioration in aerodynamics. At the same time, a structurally planeless Aircraft-Wing looks much more attractive than a traditional aircraft with a separation of the functions of the thin “carrier wing” and “cargo-passenger fuselage”. That's just for a stable flight, you still have to add a long beam to accommodate the tail, as on the giant flying wing of the ANT-20 "Maxim Gorky."
A significant expansion of the wing (increase in the chord) makes the EKIP type aircraft also clearly pronounced the Ekranoplan in its aerodynamic properties when flying near the ground. So when flying on the screen, the “fictitious body” of the wing with a large angle of attack transforms into a strange iron, where the small nasal beak of the stagnation zone on the wing inflates to the size of a huge stagnant wedge under the wing (see figure 22).
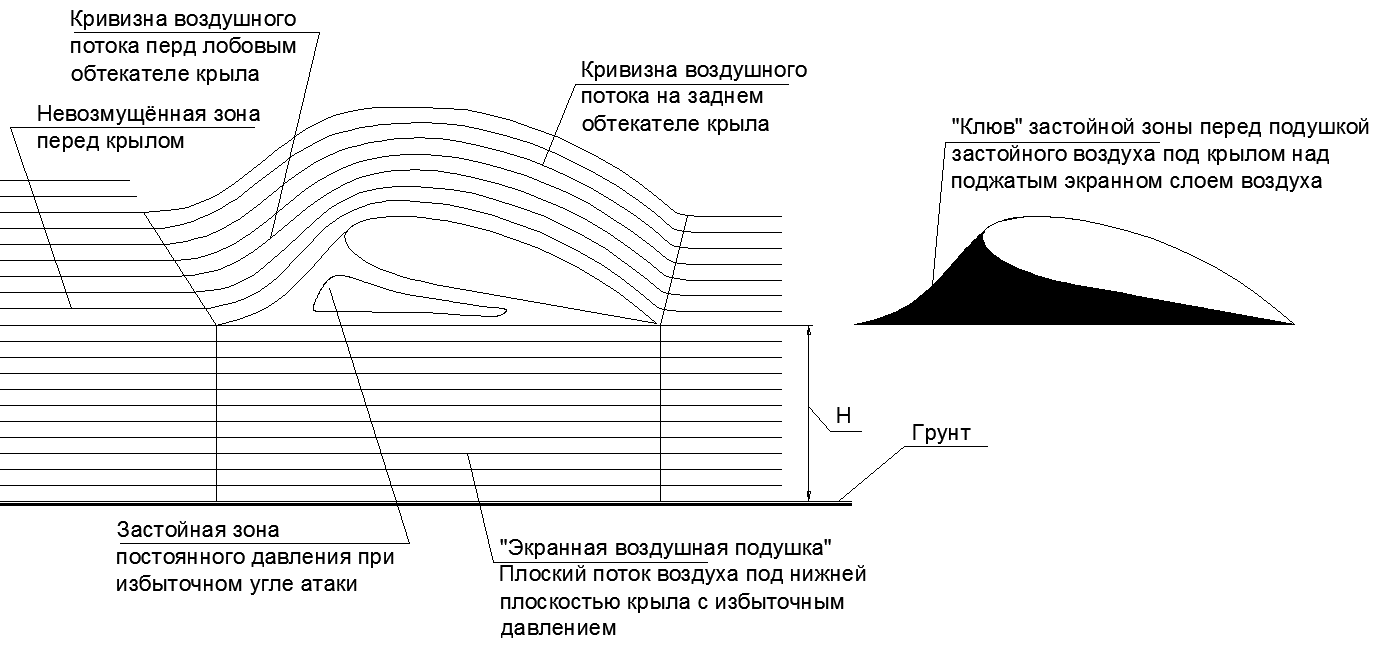
Fig.22. The profile of the wing when flying above the screen at a large angle of attack and its "fictitious body".
Inside this sharp-nosed iron can be placed as profiles of EKIP and VBA-14 (Bartini) EKRANOLET, or a super-thick wing like ANT-20 “Maxim Gorky”.
Airplanes with a very thick wing were popular in the 1930s in the USSR, when the largest pre-war ANT-20 “Maxim Gorky” aircraft was created. This aircraft had a wing so thick and wide that several cabins were placed in the root compartments of the wing, where a person walked to his full height (see Fig. 16.).
True, this monster flew with a cruising speed of only 198km / h (maximum 220km / h).
If the ANT-20 slightly shortens the wing ends, leaving only the center of the thickest part, the plane will look like the later Ekranoplan "Caspian Monster" by Rostislav Alekseev.
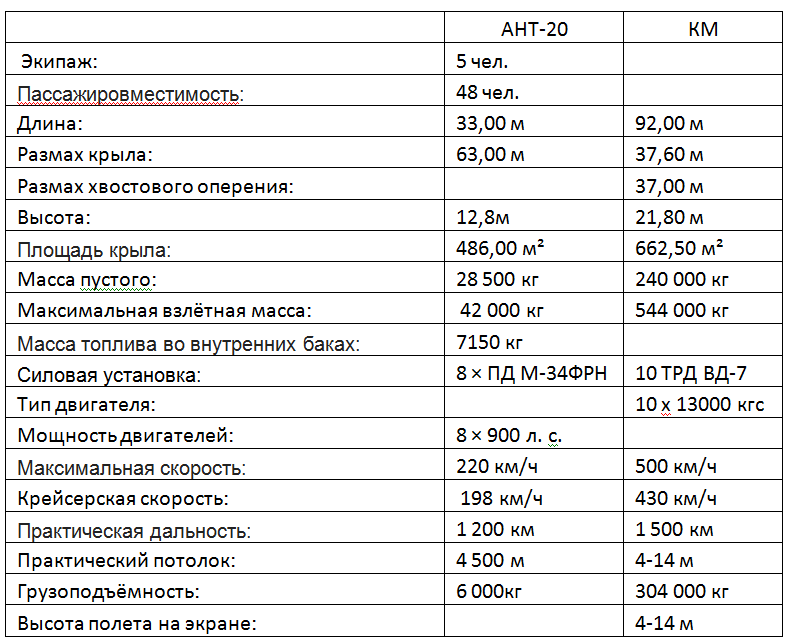
It is interesting to compare similar in size “Maxim Gorky” from the 1930s with the “Caspian Monster” from the 60s (see table 5)
Tab.5. Comparative characteristics of the ANT-20 "Maxim Gorky" 1934. and Ekranoplan CM "Caspian Monster" 1966.
The table presents reference data that must be somehow interpreted.
Let's go first simple by direct comparison of homogeneous numbers by dividing each other.
Maximum weight: 544/42 = 13 times
Wing area: 662/486 = 1.36 times
Specific load on the wing: 13 / 1.36 = 9.5 times
Cruising speed:
430/198 = 2.17 times Difference of velocity head on cruising speed: 2.17 ^ 2 = 4.71 times
Power of power installations: (10 * 1300 * 9.81 * 430 / 3.6) / (8 * 900 000 * 0.735) = 28.8 times
Payload based on fuel: 304 / (42-28.5) = 22.51.
Practical range: 1500/1200 = 1.25
The ratio of fuel efficiency ANT-20 = 7150 / (1200 * 6) = 0.993 l / (t * km) The
gluttony of the CM is not known, but it can be estimated through power and speed.
When calculating the specific consumption for reference gluttony 0.8kg / (kgf * h) for the engine of the TRD VD-7.
The consumption of afterburner during acceleration from water is 10 * 13000 * 0.8 = 104 000 kg / h.
Considering the duration of a cruise flight on the screen with only two working engines out of ten available for acceleration and exit to the Screen, the economy will increase.
For a cruise flight with two engines 2 * 13 000 * 0.8 = 20 800 kg / h
Flight time 1500/430 = 3.5 hours
During the flight to the maximum range of 1500 km, the CM will eat at least 104 * 0.5 + 3.5 * 20.8 = 100 tons of fuel.
And the payload will be about 200 tons.
Fuel economy KM will get 100 000 / (1500 * 200) = 0.333 l / (t.km).
Conclusions from the obtained ratios:
1. According to the fuel efficiency, a CM can in the optimistic version turn out to be 3 times more economical than ANT-20.
Now the modern Airbus A380 airliner has a cargo modification A380F with the ability to carry cargo up to 150 tons at a distance of up to 10,370 km. The maximum take-off weight is 560 tons (the mass of the aircraft itself is 280 tons). The calculation of profitability for the cargo version of these indicators makes 130 tons of fuel 150 tons of cargo at a distance of 10370 km: 130000 / (150 * 10370) = 0.0835 l / (t * km).
In terms of passengers, the indicator is different: “Among large liners, the most economical is three liters of fuel per passenger per hundred kilometers (54 nautical miles). According to Airbus [5], the A380 burns 17% less fuel per passenger than the “modern largest aircraft” (apparently, the Boeing 747 is meant). “
That is, when checking for 850 passengers with luggage and seats, we will get an indicator close to the calculation for the cargo version.
It turns out that we not only began to fly 4-5 times faster over the past 80 years, but also improved fuel efficiency more than 10 times from the ANT-20 and 4 times from the Ekranoplan KM. Although only 20 years ago, our Airbus flew 5 times faster than ANT-25. The recent decline in speed in passenger aviation has been caused by the struggle for fuel-efficient flight.
2. The cruising speed of the CM is made so high by force, since at a lower speed it simply cannot fly on the screen. The flight condition on the screen is the fulfillment of the inequality “Velocity pressure”> “Average load on the wing”, that is,
Pv = 8560Pa at 430km / h (120m / s)> 544000 * 9.81 / 662.5 = 8055Pa.
3. The flight safety of a low-speed Giant Aircraft from the 30s is much better than that of an excessively high-speed WIG from the 60s, almost uncontrollably carried along among slow-moving ships and omnipresent water birds.
4. The cost of operating waterfree by sea ekranoplans is much more expensive than for land high-altitude aircraft. This is due to the excess number of engines needed only to start from the water and exit to the on-screen flight, as well as due to the extreme aggressiveness of the sea water when it affects the engines and the construction of the ground-effect vehicle when flying in clouds of splashes from nearby sea waves.
5. For the WGM KM it is easy to consider the quality of the wing when flying on two engines, equal to the ratio of their thrust to the weight of the wig itself K = 544 / (13 * 2) = 20.9. Thus, the aerodynamic efficiency of a large and heavy Ekranoplan is at the level of efficiency of the best modern large aircraft with a glider quality of the order of K = 18-20.
6. The three-fold gap in efficiency of the WGM Airbus 380F remains an enigma for me: Why, with the equal quality of the glider at the Airbus, fuel efficiency is 4 times better?
Or the whole secret lies in the terrible gluttony of the old Soviet turbojet engines in comparison with modern turbofan engines of a high degree of bypass ratio?
Bibliography:
Criticism of the existing Theoretical Explanation of Lift on the wing of an aircraft
After listening to the lectures of MIPT Faculty of Aeromechanics and Flying Technique (FALT) “Introduction to Aerodynamics” and reading several different university students on “Aerodynamics” [1-3], I was puzzled by a number of obvious contradictions in the explanations of the physics of the flow around air (gas or ideal). fluid) of various solid objects and the formation of lift on the wing.
- The main replicated version of the formation of lift on the wing is the difference in the speed of air (fluid) flow above the wing and under the wing, and as a result there is a pressure drop according to the Bernoulli Law. At the same time, the Bernoulli law explicitly links the calculated flow velocity on the wing surface with instrumentally recorded pressure on the wing, ignoring other possible explanations based on at least the basic laws of physics.
- When analyzing the flow around an ideal non-viscous fluid of profiles in plane flows, we surprisingly obtained a fold increase in flow rates in comparison with the base velocity V0. That is, the law of energy conservation is refuted, since the energy for the acceleration of the flow is taken from nowhere, multiply exceeding the energy of the flow incident on the wing. At the same time, the hydrodynamic postulate is ignored, which, according to the same Bernoulli law, when the jet outflows from under the level, the velocity head is uniquely limited from above by static pressure in the vessel, that is, the velocity head of the jet after acceleration on the wing cannot exceed the static pressure compressed during deceleration of the medium.
For the flight of the modern aircraft necessary lifting power of 500-600kg / m.kv. When taking off and landing, the speed of modern aircraft is about 250km / h. In this case, the necessary lift force on the wing is ensured at a flow rate of the upper plane of the order of 450 km / h.
What is the mechanism for such acceleration of air flow without a visible mechanism for accelerating exposure to it?
After all, the contact of the wing with the oncoming flow can only lead to deceleration of the flow, but not to its acceleration!
These contradictions must be removed!
Physics should not lose physical meaning in favor of beautiful and complex mathematical constructions!
Let us consider a different explanation for the formation of wing lift without revealed violations of the laws of physics and common sense. This will require the application of the laws of ordinary mechanics.
In consideration, we consider that air consists of separate mutually repelling (for creating gas pressure) particles with their own mass, each of which obeys the laws of mechanics when its direction changes and the magnitude of the speed of movement changes.
The ambiguity of the relationship of the vacuum over the wing with increased flow
The considered real wing is not an element of an ideal tube in the model of Bernoulli's Law, but is a bounded solid object in the unlimited space of a moving real gas consisting of completely tangible in mass and size of gas particles. In this case, one should consider the curvilinear flow of the jets over the curved surface of the wing, taking into account the inertia forces and the generated pressure, perpendicular to the velocity vector and the surface of the wing.
If we consider the motion of the jets above the wing profile, then a jet of air can create a vacuum over the wing due to the curvilinearity of its current.
So for the curvature of the rectilinear motion of the body it is necessary to apply a force in the direction perpendicular to the velocity vector. In the case of a continuous flat jet for its curvature it is necessary to ensure the difference in pressure above and below it. In this case, on the side of the convexity of the jet there will be an increased pressure, and on the concave side, a reduced pressure.
When moving along the circumference of the material point, the centripetal acceleration will be created by the force
F = m * V ^ 2 / R
And with the same circular movement of a thin layer of gas of thickness dR the mass will be equal to
m = q * S * dR ,
where S is the area of the gas layer portion, q is the gas density. If we bring the centripetal force to the elementary area of the gas layer, the force will turn into pressure
P = q * V ^ 2 * dR / R
When an air jet flows along the surface of the wing, the gas layer moves along a curved path. At each point of this trajectory there is a radius of curvature, which allows you to calculate the inertial gas pressure in a direction perpendicular to the velocity.
Thus, it is possible to directly calculate the pressure (vacuum) on the wing from the layer of gas flowing above its surface, while the gas flow velocity will always be considered equal to the flight velocity of the wing Vo.
To begin with, we consider the simplest case of a wing in the form of a plate of zero thickness bent with a radius R. Such thin curved profiles are used for ultra-light gliders in aircraft modeling.
By the way, according to the usual theory with the Bernoulli law, a thin curved plate should not have any lifting force at all, since the length of the path under the wing and above the wing is the same. But the lifting force of the thin wing is, moreover, very significant, which unequivocally shows the incorrectness of the lift model using the Bernoulli law.
For an estimate calculation of the wing, we choose the profile height that is usual for low-speed airplanes 20% of the wing width. In this case, for the height of the profile, we take the difference in the heights of the leading and trailing edges in relation to the horizontal air flow (see

fig. 1-3) . Geometry of a thin wing of constant curvature

Fig.2. Estimated flow around a thin radius wing

Fig.3. Character of pressure distribution along a thin radius wing and resultant forces in directions
Then with a width of 1 m and 20% of the profile height the wing radius will be 2.6 m, provided that the tangent to the wing is horizontal at the top of the profile.
Now let's calculate the centripetal pressure on the wing from the curved air layer along the arc.
So, for a speed of 70 m / s (252 km / h), the pressure of a single layer 0.1 m thick with a radius of curvature of 2.6 m is 235.6 Pa or 24 kg / sq. M, and the value of velocity head at 70 m / s is 3063 Pa.
If we take into account that a thin wing has a flow around it from two sides, then these values need to be at least doubled, and then multiplied by a number of parallel layers, also bent by a moving wing. If we assume that the thickness of the perturbed layer is not less than half the width of the wing on each side of the wing, then we obtain a total redoubled load on the wing of about 2,356 Pa. These figures are perfectly beaten with the values of loads on the wing for low-speed light aircraft with a thick wing and a similar surface curvature of the wing. (see tab.1)
Since the pressure Pcr is applied to the curvilinear surface of the thin plate, the force Fcr from Pcr can be decomposed into Lifting force Fy and into force Resistance to flight Fx.
The lift force Fy is equal to the integral of the projection on the Y axis of forces from the Curvilinear flow pressure Rcr over the entire area of the wing.
In the case of uniform pressure on the pivoting wing, the value of Fy will be equal to the product of Pcr and the area of the projection of the wing to the X axis, which is equal to S = B * L of the wing (in this case, 1 sq. M.).
Fy = Pcr * Bcr = 2356 * 1 = 2356 N / m.
At the same time, the resistance to horizontal movement in this case will be equal to the integral of the projection dFcr on the X axis over the entire area of the wing. In the case of uniform pressure on the wing, the value of Fx will be equal to the product of Rcr and the area of the projection of the wing on the Y axis, which is equal to the height H of the wing profile (in this case, 0.2 square meters).
Fx = Pcr * Ncr = 2356 * 0.2 = 462 N / m.
At the same time, we obtain К = Fy / Fx = (Ркр * Bкр) / (Ркр * Нкр) = Bкр / Нкр, that is, with uniform pressure on the circular thin profile, the quality of the wing is equal to the ratio of only the geometric parameters of the profile К = В / Н.
According to the rule of vector decomposition of forces from a given picture, you can immediately get the value of the quality of the wing K = Fy / Fx, which in this case is equal to K = 100 * Pcr / 20 * Pcr = 5.
Interestingly, if you scale this design wing in the direction of a tenfold decrease (along the radius of curvature, height and width of the profile), then the pressure on the wing will remain unchanged at equal flight speeds (see table 2). It is for this reason that heavy cruise missiles fly on fairly small thin wings. It turns out that their small in size and thin wings with sufficient curvature is really enough to create the necessary lift!
Since room modeling is quite cheap, these numbers are rather simply checked on full-scale models.
Tab.1. The pressure of the curved air layers on the wing of constant radius R = 2.6 m, depending on the speed of flight.

Tab.2. The pressure of the curved air layers on the wing of a constant radius R = 0.26 m, depending on the speed of flight.

It is interesting to consider how the wing CRC changes with its constant curvature Rcr, but with the variable parameter of the Wcr profile width. (See tab.3)
In the very first line of the table, the aerodynamic quality of the wing reaches a fantastic value of K = 182, but the wing load is only 67 Pa (7kgs / sq.m), which is suitable only for room model gliders.
The required lift force on the wing arises only when the wing K is sufficiently small, as can be seen from the last lines of the table.
Yellow indicates the column of the variable parameter and the line of the original profile with CRC = 5.
Tab.3. Changes in wing parameters of constant radius R = 2.6 m at various profile angles (profile width) at a constant flight speed.

You can also calculate the change in lift force Fy and the wing quality Kkr for a wing with a constant chord, but different wing curvature at a constant speed. The yellow columns are: Variable argument Rcr - radius of curvature and constant width of the profile Wcr. Also highlighted line of the original profile with CRC = 5.
Tab.4. Changing the parameters of the wing of a variable radius of curvature at a constant width of the profile B = 1 m at a constant speed of flight.

In the described model, to obtain a vacuum above the wing does not require additional acceleration of air above the wing. A noticeable discharge above the wing is provided in conditions of a significant curvature of the air stream flowing around the wing under the action of static air pressure forces of the entire surrounding space. The angle of inclination of the chord of the original curved plate is 11.3 degrees (half the angle of the arc segment at 22.6 degrees), which is in good agreement with the landing modes of the wing of modern airliners when landing with the wing mechanization released (slats + flaps). In the landing mode, the wing with the released mechanization is much more like the case of a curved thin plate considered than the classical wing with a straight lower plane (see figure 4).

Fig.4. Wing asymmetric profile with a flat bottom streamlined surface: a) straightened position for high-speed flight; b) a wing with maximum curvature with fully released mechanization.
Strongly curved thin wing is widely used as fan blades. Low linear velocities at low pressures make it possible to use thin steel or plastic plates of extremely small thickness in the fans as blades, as their strength is sufficient to withstand the existing loads.
In heavy aircraft, the use of thin wings is technically impossible due to their insufficient strength. The large thickness of the wing allows you to place inside the wing sufficiently high load-bearing beams of sufficient strength and rigidity for bending and torsion, while maintaining an acceptable weight for the aircraft. It is for this reason that all the aerodynamics is studying the wings with quite tangible thickness. For this reason, we move from considering the aerodynamics of a thin curved plate to a wing profile with real thickness and planes of different curvature.
At the end of the consideration of the thin-wing flow model, it is necessary to present one more proof of the efficiency of the proposed model for explaining the “Wing lift”. As is known from mechanics, Force is the change in momentum per unit time, that is,
F = d (m * V) / dT
In the voiced model of a thin curvilinear wing flow, we can calculate lift force Fy as a change in the vertical air flow pulse, which is counted as
Fy2 = (dR * 10 * q * Vo) * Vo * sinAcr ,
Where Vo is the wing velocity, dR is the thickness an elementary curved layer of air flow in the design model; 10 is the number of simultaneously curved layers; Acr is the angle of the flow from the wing to the direction of the initial velocity Vo.
After carrying out the calculation we get that both calculations give the same result.
Or in analytical form:
Fy1 = Pcr * Bcr ,
Pcr = (dR * 10 * q * Vo) * Vo / R ,
Bcr = R * sinAc By
substituting the sweep Pcr and Bcr into the expression for Fy1 and reducing the like R in the numerator and denominator, we will receive:
Fy = Ркр * Bкр = (dR * 10 * q * Vo) * Vo * sinАкр
And it means that the equality is always true Fy = Fy1 = Fy2
That is, the “Inertial-curvilinear” method of calculating the “Lift Force” of the wing gives a formula that is identical with the method “Reactive “Impulse Force” for a wing of the same geometry.
This means that airplanes do not fly due to some kind of “magic” force from the “magic whirlwinds”, but due to the old and understandable “Impulse of Power” or “Reactive thrust” when the air mass is dropped down.
Thick Wing
At low flight speeds during takeoff and landing (M = 0.2 or 250 km / h), the velocity head does not exceed 3 kPa (3% of the atmospheric pressure at sea level at 100 kPa), that is, it is so small in relation to the basic atmospheric pressure that Geometric compression of the flow becomes visually undetectable when drawing a jet stream at the wing.
To create a lift above the wing, it is necessary to create a curvature of the flow so that the wing is in the area of the concavity of the air flow. To ensure such a curvature of the jet above the wing helps the curvature of the upper plane of the wing, located in the aerodynamic shadow of the nose fairing.
In this case, the lower plane of the wing is flown either in a straight line without creating a vacuum, or over a concave surface, rejecting the flow of air downwards, which creates a positive increase in pressure on the wing from below and is summed up with the lifting force from the vacuum above the wing.
The main difference between a thick wing and a thin plate in our case will be the appearance of a frontal fairing, pushing the opposite air flow before it reaches the curved planes that create lift.
A braking zone occurs in front of the flying thick wing, where the velocity of the air becomes zero (relative to the wing), and the overpressure in this zone is equal to the velocity head Pvo.
Drawing current lines without taking into account air compression will not work, otherwise you will have to either accept the version of the acceleration of air above the surface of the wing, or the zone of influence with curvature of the flow will rush to infinity in an incompressible medium, which is implausible.
By the way, both effects (Acceleration of the flow and Infinite zone of influence in incompressible liquids) manifest themselves in practice in wind tunnels with smoke current lines and during the movement of submarines at shallow depths.
So in wind tunnels (ADT), the flow around the test mock-ups occurs with a noticeable acceleration of the flow (reduction of the thickness of the smoke lines) in the gap wall of the ADT layout. That's just the interpretation of this phenomenon is completely incorrectly attributed to the acceleration of the flow for the formation of lift. In fact, the acceleration of flow in the gap “wall ADT layout” is simply a consequence of narrowing the flow area in the flow path of the ADT while maintaining a constant air flow in the ADT itself due to powerful fans with a hard fan characteristic.
When submarines move at shallow depths above the submarine, a visually noticeable water hump forms. The size of this hump is equal to the volume of water in front of the hull of the submarine, which must somehow be moved from the area in front of the submarine to the stern when moving at a given speed. A hump on the surface is also formed when the submarine moves at great depths, but due to the larger spreading area of the hump, its height becomes undetectable with simple visual observation. The cause of the water hump on the surface is explained by the inability to move the incompressible fluid towards the bottom, and a thin layer of water under the atmospheric pressure of the air becomes Easily Shifted, with an understandable elastic characteristic of the Atmospheric pressure and Forces. By the way
Thus, we assume that the gas is compressible, and the zone of influence from the wing bending around is made dependent on the magnitude of the compression of the jet on the pressure Pvo.
The pressure in the stagnation zone at the fairing is maintained by curved air jets enveloping the fairing. The connection of pressure with the curvature of the layers of air is the same as in the case of a thin curved wing dP = q * Vo ^ 2 * dR / RSl.
The magnitude of the zone of influence, where the curvature of the flow is noticeable, is also related to the magnitude of Vcr and Ncr. An increase in pressure in front of the fairing will be compensated by a decrease in pressure in the wake behind the wing, that is, the wing forms a linear dipole in pressure, which at a great distance practically ceases to affect the surrounding air space at low (subsonic) flight speeds.
If you take the shape of a round nose cone, then half the profile height will be equal to Ncr / 2 = Rlob.
We consider that the stagnation zone with pressure Pvo is entirely created by the curvature of the layer within the width of the Vcr profile, then we can estimate the radius of curvature of the jet with a thickness of Ncr / 2 = Rlob.
It is necessary to fulfill the condition Pr = Рvo.
Therefore
qVo ^ 2 * Rlob / R = qVo ^ 2/2
After reducing the same terms of density and speed, respectively, in the left and right side of the equation we get
R = 2 * Rlob
Thus, it turns out that the limiting radii of the flow curvature are limited solely by the curvature of the fairing ( local profile height), and it does not depend on speed.
When turning the incident jet to bypass the profile, a situation inevitably arises in which the boundary jet with the zero flow line touches the fairing. At this touch point, the flow velocity is directed away from the wing, and the flow curve reaches the inflection point. That is, at this point, the separation of the layer from the wing occurs with a change in the direction of convexity of the curvature of the jet (see figure 5).

Fig.5. Interaction of the incident flow Vo with the front wing fairing.
At high flight speeds, the magnitude of the velocity head Pvo is so large that the jet breaks off from the nose fairing and, having described a long arc above the wing plane, returns back to the wing surface.
At the point of return of the torn off jet to the plane of the wing, an Impact occurs, and the jet abruptly changes direction to be tangent to the plane of the wing. In this case, under the arc of a flying jet from the separation point to the return point, a closed low-pressure cavity arises. (see figure 6).
In the traditional “Bernoulli Aerodynamics”, the described formation of a developed detachable bubble with a strong discharge and a shock return of the detachable jet is explained as follows: “... At high pre-sonic and transonic speeds, acceleration of air flow over the wing to supersonic values occurs, resulting in pressure over the wing being greatly reduced, and then there is a jump in pressure (the impact of the transition to supersonic), with the transition after it to a subsonic flow ... ". Such an explanation looks like an obvious stretch of real experimental data on an inconsistent theory.
Since the fairing divides the incident flow into two parts along the zero line, flow separation occurs on both planes of the wing. But due to the different directions of the planes with respect to the flow (to the flow or in the aerodynamic shadow), the tear-off discharge bubbles above and below the wing have a different size, and the impact force of the return jet changes in proportion to the size of the tear-off bubble.
On the basis of such a distribution, the pressure diagrams on the front wing fairing and the obtained CRC qualities of thin radius wing plates depending on the relative thickness of the Vrc / Ncr profile. It is easy to understand the causes and patterns of such a phenomenon as “streamlined” of various geometric shapes (see Figure Cx in Figure 6).
It would also be extremely interesting to consider the pressure diagrams for the flow around the standard axially symmetric bodies around the jet stream and obtain their cross-sections X and X along the sections, and not just one total coefficient X for the figure as a whole.

Fig.6. The flow of air around the thick wing with the designated characteristic elements of the movement. The diagram of pressures on the wing and diagrams of the pressure coefficient Su on the chord of the wing and Cx on the height of the wing. The area of the shaded zones corresponds to the total forces in the Y and X directions, respectively.
At low M numbers, the main lift force is formed in the zone of the nose fairing in tear-off bubbles. At low M numbers, the return jet in the separation zone goes tangentially to the thick profile of the wing and does not cause an Impact at the return point. But when approaching M = 1, tear-off bubbles inflate so much that it becomes impossible to achieve the desired profile thickness for a continuous flow of the jet, and then a pronounced separation of the flow occurs with the formation of a tear-off bubble visually observed from the vibrations of the silks glued to the wing plane. The expansion of tear-off bubbles in height becomes an obstacle to speeding, and therefore their development begins to decrease due to the sharpening of the nasal edge (lowering the radius of the frontal fairing).
At transonic flight speeds, the rear border of the detachable bubble reaches the trailing edge of the wing, after which the volumes of the upper tear-off bubble are connected to the high-pressure zone of the lower plane of the wing. In the combined volumes of the upper and lower tear-off bubbles, the pressure levels off, and the lift force of the wing Fy drops sharply.
During supersonic flight, the wing of the usual drop-shaped form becomes completely inapplicable, but instead a wing with a developed sharp “beak” appears, on which the main part of the lifting force is now created, with the possibility of a tear-off bubble being minimized.
To ensure the landing modes of flight at low Mach numbers in the “thin-beak” wing, the front and rear deflected mechanization are installed (see figure 7). This type of thin wings with sharp leading edges and deflected front and rear mechanization are put on combat fighters of 4-5 generations (see photo 1-2). When the mechanization deviates downward, the “thin-billed” wing becomes close to the flow characteristics of a thin curved plate, which allows taking off and landing at low speeds and with a short run on the runway. In the future, it is possible to switch to rotate the plane of the wing entirely when performing maneuvers at low speeds, as has already been done with the fully turning tail of fighters.

Fig.7. The thin-wing profile H / B = 0.1 (10%) with a sharp rejectable “Beak” and a wide flap that can be deflected: a) a straightened position for supersonic flight; b) the deviation of mechanization down for flying at low speeds and in landing mode with large angles of attack.

Photo.1. Su-35 at a large angle of attack with rejected slats and flaps in landing mode (landing gear released).

Photo.2. MiG-29 with deflected slats and flaps in take-off and landing mode at high angle of attack and low speed (landing gear released).

Photo.3. MiG-29 on takeoff with full deflection down the front and rear wing mechanization.
The photo (see photo 3) clearly shows the shape of the “sharp-billed” slat in cross section: a flat lower edge and a radial upper edge. The leading edge itself is not sharp, but has a very specific small radius, thereby improving the aerodynamics of subsonic flight. Controlling the inclination of the slat to the incident flow allows you to optimize the mode of formation of the tear-off bubble at low speeds, creating the conditions for its unseparated collapse. Also, given the aerobatic maneuvers with the possibility of a long flight upside down, the slant deflected upwards makes it possible to reverse the deflection of a flat thin wing for a completely effective flight in an inverted position, although with worse aerodynamics than in the normal position. On later Su-35 and Su-57 planes, the leading edge is sharper and more symmetrically wedge-shaped,
Eddy formation and wing vortex drag
In the network, you can find a lot of explanatory material on any issue, including the Vortex formation on the wing of the aircraft, for example:

At the same time, it is easy to find photos of the vortex tracks from airplanes in the cloud layers that demonstrate a much larger scale of the phenomenon than they are trying to show this to us in theory

Photo.4. Vortex trail in the layer of fog for flying at a height of the plane. The rings of the visible fog vortex are hundreds of meters away from the aircraft, and visual proximity is an optical illusion created by a long-focus telephoto lens when shooting an airplane from a distance of several kilometers.

Photo.5. Vortex trail in the layer of fog for flying at a height of the plane. One can see the vertical air flow and the air waves approaching from the sides, spiraling in contact with the vertical downward flow.

Photo.6. Vortex trail in a layer of fog over the runway behind the landing plane.
These huge satellite vortices behind the planes are not formed at all at the expense of end vortices on the wing. Trailing vortices exist, of course, but their role is not so great, and aircraft designers are actively and successfully fighting it.
Large-scale eddies from photos are already forming far behind the plane, when the air wave thrown by the plane down is replaced from two sides by the flow of air from under the descending layer into the rarefied space from above (see photo 4-5). This explanation of the formation of a cocurrent vortex echoes the already considered issue of the “zone of influence of the wing on the surrounding space”. At the same time, the role of the earth’s surface lies in the boundary of the downward flow of air thrown down by the wing. That is, the flight of the aircraft and the creation of a “wing lift” is possible even in the absence of solid underlying surfaces, but at the same time the air stream thrown down will move infinitely long downward, losing speed and kinetic energy with distance, but keeping the vertical impulse unchanged. The kinetic energy of the original rejected air mass will be lost to the involvement in the movement of lateral air flows, the symmetrical multidirection of which will not change the initial total impulse created by the aircraft wing. A vivid illustration of the role of the Earth-Restrictor is Photo.6. There, the straight-line current of fog above the landing Airbus (see photo 6) descends to the ground in a straight line and only then far behind the plane begins a shift to the sides along the limiter-ground, and the layers of fog from the sides and from above already approach the middle of the cobweb, twisting in dual self-compensating spiral downward flow. A vivid illustration of the role of the Earth-Restrictor is Photo.6. There, the straight-line current of fog above the landing Airbus (see photo 6) descends to the ground in a straight line and only then far behind the plane begins a shift to the sides along the limiter-ground, and the layers of fog from the sides and from above already approach the middle of the cobweb, twisting in dual self-compensating spiral downward flow. A vivid illustration of the role of the Earth-Restrictor is Photo.6. There, the straight-line current of fog above the landing Airbus (see photo 6) descends to the ground in a straight line and only then far behind the plane begins a shift to the sides along the limiter-ground, and the layers of fog from the sides and from above already approach the middle of the cobweb, twisting in dual self-compensating spiral downward flow.
"Screen Effect" when flying wing near the Earth
In the light of the stated role of the Earth in the formation of the “Lift Force of the Wing”, it makes sense to additionally consider the “Screen Effect”, which cannot exist without the presence of a solid earth surface. Thus, the physics of the Flight of the wing in the Endless airspace and on the “Screen Effect” near the Earth has a very different nature.
Explanations of the effect of "Ekranoplan" based on the compressibility of gas at low Mach numbers
The effect of the close-lying surface of the earth on the wing lift is called the “screen effect”. With this effect, the lifting force of the wing increases dramatically when flying near a solid surface (ground, water) at a height comparable to that of the wing chord. Based on this effect, even a whole class of low-flying "Ekranoplans" appeared.
What is the essence of the phenomenon? Deal with this issue can only be assuming that the air is a compressible gas.
Then, when the wing is flying over the surface of the earth, an air gap of limited size is formed between two solid surfaces. When flying a wing with a small positive angle of attack, the counter-flow of air under the wing experiences a gradual compression from the leading edge of the wing to the trailing edge (see figure 8).
The maximum pressure of the compression on the flow screen under the wing depends only on the velocity head relative to the flying wing, and this pressure in the compressed layer cannot exceed the pressure of the velocity head of air:
Po = Vo ^ 2 * Q / 2 ,
where Rope velocity of air at wing speed Vо, Vо-flight speed of the wing, Q-density of air.
Knowing the maximum pressure increment under the wing, we calculate the geometrical parameters in the airbag gap.
So at a speed of 40 m / s (144 km / h), the velocity head Ro = 1kPa or 1% of 1 atm. (100kPa).
That is, at a speed of 40 m / s, the maximum pressure under the wing is achieved with compression of 1% over the height X of the gap from the leading edge of the wing to the rear. Such preload is almost undetectable to the eye, and the layer under the wing visually appears flat (see figure 8.a).
The angle of attack will be A = (Ro / Ratm) * X / B radians (at small angles sinA = A),
where B is the wing chord, X is the air gap to the ground below the wing at the trailing edge of the wing, Ro-speed air pressure at wing speed Vо, Ratm - atmospheric pressure (at sea level Ratm = 100 kPa).
It turns out that the maximum effective angle of attack for obtaining a screen effect depends on the height of the flight of the wing above the surface, the structural width of the wing and a given flight speed, and the angle of attack is only a derivative of these quantities.
Conclusion: It is possible to increase the width of the wing almost infinitely, reducing the angle of attack to almost zero, thereby achieving the minimum resistance Cx with the inductive component of resistance almost zero.
The “screen effect” at low flight speeds provides a very high wing quality, as it creates the maximum specific lifting force on the wing, equal to the velocity head Po at extremely low angles of attack on a practically flat and very thin wing. The quality of the wing at low Mach numbers when flying on the screen can reach a value of K = 25-30.
The contribution of rarefaction above the upper convex surface of the wing during such a flight on a “screen” with a flat wing is sufficiently small compared to the pressure under the wing.
When the flight speed increases, the velocity head grows quadratically, and to obtain the maximum screen effect, it is necessary to raise the angle of attack in proportion to the velocity head Po growth.
That is, increasing the speed of Vo in order to increase P entails an increase in speed of the Attack Angle that is quadratic in speed, which in turn dramatically reduces the quality of the wing. And starting with a certain speed Vo-max, the magnitude of the screen effect with a large angle of attack is compared with the lift of a conventional airliner in a landing mode with extended wing mechanization.
For any wing with a chord B to increase the height of flight X, it is necessary to lift the angle of attack, after which the Ekranoplan rises to some new height X2, where the balance of the degree of preload of the jet is again established due to the new angle of attack at the new height. At the same time, with increasing altitude, the flight of a ground-effect vehicle begins to linearly increase the resistance to flight and the corresponding thrust force corresponding to it also increases without changing the flight speed. That is, the fuel efficiency of the flight of an airplane can drastically change from a rise in height of only a few meters. For example, the maximum flight range of the Oriole ecologolet at a height of 0.8 m is 1,150 km, and at an altitude of 0.3 meters with the same load - already 1,480 km.

Fig.8. Airflow configurations on the “Screen Effect”: a.) Optimal angle of attack without a stagnant zone under the wing, b.) Excessive angle of attack, forming a large bubble of stagnant high-pressure air between the wing and the pre-loaded air layer of the “Screen Airbag”.
Conclusion: Additional tearing up of the angle of attack of the wing without increasing the flight speed on the screen does not increase the lift force, but only increases the flight resistance of Cx (see figure 8.b)
Considering the angle of the airliner’s chord in the landing mode about 15 degrees we can estimate the amount of jet compression under the wing to the pressure Ро and the corresponding speed Vо, considering the value of the chord B to be equal to the height of the flight of the wing X.
15 degrees corresponds to sin15 = 0.262
At an angle of attack of 15 degrees, there should be a speed head Ro = 0.26 atm = 26 kPa, but such pressures are realized at very high speeds (740 km / h) and far exceed the calculated wing loads required for flight. That is, such a large landing angle of attack to create a screen effect over the runway is excessive at landing speeds of 250-300 km / h.
The quality of the wing at an angle of attack of 15 degrees will drop to the value of just K = 3.7.
The landing speed of the airliner is only about 250 km / h (70m / s), while the velocity head will be Ro = 3kPa or only 3% of Rathm, while the design load on the wing in flight is normal to 5kPa (500kg / m.kv = 5% of Ratm). That is, when landing, the screen effect of an airliner begins to be noticeably felt by the pilot at a height comparable with the width of the wing B, comparable to the height of the landing gear. Leveling the aircraft and reducing the angle of attack for a speed of 250 km / h allows the aircraft to penetrate the “screen airbag”, since its carrying capacity is lower than the required pressure under the wing for flight.
Due to the “Screen Effect”, there is an “incompatibility” on an airplane in horizontal flight without releasing wing mechanization at an attack angle of 5% (or 3 degrees) with a speed head Ro = 5 kPa, which corresponds to Vo = 324km / h or 90m / s.
The angle of attack of 5% (or 3 degrees.) Creates the quality of the winged wig equal to K = 20.
High K = 30 corresponds to an angle of attack of 3% (2 degrees), while the support under the wing will be only 3% * Ratm = 3 kPa (300kg / sq.m), which corresponds to the velocity head at Vo = 70m / s (250 km / h)
Thus, cost-effective flight modes in the mode of "WIG" in comparison with the usual high-altitude "plane" lie in the zone of low speeds. When the wing wing quality drops below K = 20, it is more profitable to use ordinary high-altitude aircraft for transportation. That is, the cost-effective areas of operation of Ekranoplan correspond to speeds below 300km / h.
Maneuvering Ekranoplan
Separate consideration deserves the question of maneuvering Ekranoplan in flight. Since the wing lifting force on the “screen” is formed differently than during high-altitude flight, it cannot maneuver the “in-flight” ekranoplan.
An ekranoplan cannot lay bends with a roll on the wing, as it will immediately receive a loss of lift on the raised wing and touching the water with the wing lowered. For ekranoplan, rotation is possible only with a “pancake”, that is, completely without a roll, but only due to the creation of lateral forces from the vertical tail.
The vertical tail of the Ekranoplan itself should also be different from the aircraft tail. The Ekranoplan vertical tail should consist of at least two keels, capable of working both synchronously and separately, depending on the type of maneuver being performed. At the same time, the vertical tail unit not only turns the Ekranoplan around its vertical axis, but also creates a horizontal force across the direction of flight speed.
The horizontal tail fin on the rear keel adjusts to the angle of attack.
The wide and short wing must be equipped with developed end-washers, skegs, which keep the flow pressed under the wing from spreading to the sides. Additionally, these skeg washers serve as landing pontoons for landing.
You also need additional horizontal tail at the ends of the main wing to compensate for the overturning moment from the action of the vertical tail.
Practically according to this Scheme, the Bartini VVA-14 ekranoplan was built (see figure 9) and numerous versions of the EKP-airplane perspective layouts, where the side-tail washers play the role of the front vertical tail (see figure 10).

but.

b.

at.
Fig.9 Ekranoplan Bartini VVA-14. A. Drawing. b. Model in 3-D. at. Photo of the current sample on the water.

Fig.10. Layout of a promising large wig.
Types of maneuvers wig due to the vertical tail:
- Two identical spaced keels provide the “Side Shift” mode for simultaneous rotation in one direction. In this case, the Ekranoplan shifts from one lane to another without rotation of the body. In this case, the horizontal plumage works in different directions, compensating for the heeling moment from the vertical tail.
- If the keels are rotated in different directions at the same angle, then there will be a turning moment that rotates the body of the Ekranoplan around a vertical axis. In this case, the horizontal tail does not work, since the moment from the vertical tail does not occur.
- If the keels are rotated in different directions to different agreed angles, a rotation will occur along a circular trajectory (circulation), where the velocity vector coincides with the direction of the longitudinal axis of the Ekranoplan fuselage, and the ekranoplan flies along a predetermined circular trajectory with equal angular velocities of flight and rotation of the WIG itself around vertical axis.
In this case, the horizontal plumage works in different directions, compensating for the heeling moment from the vertical tail.
All these modes are practically little realizable in manual mode, since the low altitude simply leaves no time for reaction in the pace of human perception. To control the ekranoplan, automation control is needed, similar to the automatic stabilization of ultra-unstable 4-5 generation fighters.
Conclusion
All the above assumptions are based on openly published experimental data (pressure drop diagrams on the wing and other data obtained on ADT).
For experimental Aerodynamics for the last century, huge sums of money were invested in building ADTs of various types and sizes, as well as a huge amount of factual material was obtained in experiments with models of various aircraft and individual wing elements.
It is surprising that in the process of teaching students rely not on the materials of actual Experiments, but on dubious theories 100 years ago. And this is despite the fact that the experimental data themselves clearly contradict these mossy Theories.
Even in such a generalized introductory course as “Introduction to Aerodynamics” for PhALT Phystech, qualitative explanatory models of the basic concept of “Wing Lifting Force” are not given, but superseded by abstruse science-like juggling with mathematical formulas (which also do not allow to calculate anything).
In science, there has been a trend towards a split between theory and practical engineering application in the development of specific products. Explicit contradictions in the theoretical models are not advertised, but on the contrary they are silently silenced in order not to shake the authority of mossy and already deceased elders from the Academy of Sciences and not to interrupt the triumphant march of their sincere delusions through the pages of quite modern textbooks and monographs.
Wing lift. Part 2
Ilya Alekseevich Monin, Ph.D., imoninpgd@gmail.com
In order to understand the development of “aviation” as an industry and “aerodynamics” as a science, you need to remember that first appeared the first aircraft built by on-the-spot engineers (see fig.11), and only then theorists began to emerge who created the discipline “Aerodynamics” based on the results of the creation of design engineers.
In the picture is a plane created by motorist Henri Farman, a remake of a purchased small-scale Voisen plane. At the same time, the original aircraft of the Vuazen brothers began to be produced only in 1907. At the time of purchase by Farman, the airplanes of Voisin could only jump slightly and jump several dozen meters. Farman, after a series of alterations of the original aircraft, made it possible to fly more than 1000m, while still turning around and, making a circle, land. There was a record flight Farman January 13, 1908. And in 1909, the Farman Brothers firm opened its own production of airplanes of its own design and a flight school for teaching the art of flying on them (see figure 12). The flight speed of the Farman aircraft was then about 60 km / h, which was shown in a record flight at a distance of 180 km, overcome in 3 hours of flight.

Fig.11. Layout of the aircraft Vuazen, converted to a record flight Farman in 1907-1908gg.


Fig.12. Layout of the aircraft "Farman IV-1910." In the museum, and a photo of the original sample at the airport.
It is clear that the first early aircraft were thin, light and low-speed.
These are the parameters that correspond to the first convex-concave thin profiles, more similar to the simplest curved sheet of plywood, and not to a complex profile with a deep theoretical miscalculation.
For reference, I give an illustration of the transformation of wing profiles from the earliest beginning of the 20th century, to the fully developed aircraft industry of the mid-40s. (see

figure 13) Fig.13. Trends in the profile of the wing of the aircraft of the first half of the 20th century.
After the first light experimental aircraft was followed by a rapid increase in the size and mass of aircraft for the transport of ever-increasing payload. Thin wings could not withstand such a scale and weight, which required installing high strong beams inside the wing, and making the wing itself flat-convex or even double-convex to hide the supporting beam behind the streamlined wing sheathing.
Already in the 20s, all wing profiles took quite a modern look.
By the 1940s, the aviation industry had developed so much that it began to produce whole armada of airplanes capable of carrying entire cities into the dust of the air. But with such an explosive development of production capacity, the theoretical base remained extremely weak.
By the 1930s, the intensity of aviation development did not allow building new airplanes according to the “intuition”, but required the construction of a powerful experimental base for blowing parts of airplanes, large-scale mock-ups and airplanes entirely on the ground in huge wind tunnels (ADT).
So in TsAGI in 1939, the largest at that time (the second in the world now) wind tunnel T-101 was launched, which allowed to explore on the ground entirely on actual flight speeds at that time.
Flow rate 5–52 m / s
Number of Re per 1 m to 3.6 ∙ 106
Total atmospheric pressure
Speed head up to 1.7 kPa
Ambient deceleration temperature
Angle of attack range (α) ± 20 °
Slip angle range (β) ± 180 °
Dimensions of the working part :
Nozzle section (ellipse) 24x14 m
Working part length 24 m
Sizes of test objects:
Wingspan: up to 18 m
Fuselage length: up to 30 m
Wing area: up to 35 m2
Since then, the airplanes have become much larger, and the flight speeds are much faster, so that not a single modern aircraft fits into the T-101 ADT entirely, and in more modern and more high-speed ADTs, they only blow large-scale dummies or structural elements separately.
True, in theory, since the beginning of the last century, little has changed, so that already at the end of the twentieth century, aircraft designers began to reinvent what designers in the early to mid-20th century had passed, but theorists did not explain. For example, let me give a view of the profile of the wing of the aerobatic plane, which was considered the best in the 1980s (see figure 14).

Fig.14. One of the wing profiles from the Aviation Profiles catalog.
The same recurring course of thought is observed among large samples of flight technology, this was reflected in the creation of WIG monsters in the 1960s and 80s (Fig. 15), little distinguishable from the giant planes of the late 1930s (Fig. 16).
At the same time, the screen effect itself was discovered as early as the beginning of the 30s at the time of landing large multi-engine aircraft with a large wing chord.
The same screen effect clearly manifested itself when landing a record long-distance ANT-25 aircraft, when during a test flight in 1933, the plane simply could not land, and with a light touch of the wheels of the ground, the plane jumped up and took off again. In order to remove this effect and ensure a smooth landing, it was even necessary to install special retractable brake flaps, which sharply worsen the flight performance of the wing during landing.
The wing chord in the widest root part of the ANT-25 exceeded the height of the landing gear, thus creating ideal conditions for the formation of a screen effect under a wide low-flying wing. Moreover, during landing with empty tanks with an aircraft mass of 4000 kg and a wing area of 88 square meters, the average load on the wing in flight was less than 50 kg / square meter, which corresponds to the velocity head 500 Pa created at a speed of 104 km / h (29 m / s) for flying on the screen. It is worth noting that the aircraft of that time flew extremely slowly (by modern standards), so the record ANT-25 had a cruising speed of about 165 km / h (max. 266 km / h at altitude), with a flight range of 10-12 thousand km and a duration of 75- 80 hours in a row.
A.

B.

C.

Figure 15. The ekranoplan "Caspian Monster": a.) In flight. B.) Stationary on the water full face. c.) Motionless in frontal projection.
A.

B.


Fig.16. Giant ANT-20 "Maxim Gorky", 1939. a) Sketchy section. B) Photos at the airport and during landing.
Stagnation zones in air flow around bodies of complex shape as a tool for forming a virtual wing profile.
Often there are cases. When it is necessary to build airflow lines around bodies, the shape of which is difficult to call streamlined.
It is clear that the air will not obediently wrap around all the corners and notches of the body, but will go in soft twists, sweeping over the pits and filling them with vortexes of detached streams of stagnant zones.
If we consider the presence of stagnation zones as additional solid volumes of the profile itself, then the flow around the aerodynamic elements known to us will take a completely different form.
Interestingly, this method of finding the equivalent conditional prototype wing is used in existing applied Aerodynamics. In any case, the method of constructing a “Fictitious semi-infinite body” around a rigid wing is described in the textbook [3] for three whole pages (pp. 435-437), while choosing the border of the fictitious wing as the boundaries of the thick hindered boundary layer, that is, adding to the wing our very stagnant zones in the "tear-off bubbles" or turbulent zones with a complete disruption of the flow above the wing. The pressure on the solid wing from the high-speed air flow is considered to be equal to the pressure of this flow on the “fictitious body”. It turns out that the pressure is transferred from the speed jet to the solid wing through a sufficiently thick layer of slow-moving air of the boundary inhibited layer (stagnant zone) without any distortion.
Let us consider in detail the process of soft flow around high-speed jets of varying intensity of wing profiles and select various “stagnant zones”.
The case of full sticking of the flow to the wing at small angles of attack does not add any specialty (see figure 17), but a small stagnant zone appears on the front fairing, resembling a small sharp beak on a round bird head.
The element seems small, but it is extremely important to understand the phenomenon of “flow” in general.
Consider the usual profile of a wing in horizontal flight with pronounced tear-off jets, first with a zero angle of attack (see figure 18), and then the same wing is already at a large angle of attack (see figure 20).

Fig.17. The profile of the wing with a flow without breaks on the planes of the wing, but with a small zone of complete deceleration of the flow on the nose of the wing.

Fig.18. The profile of the wing with the separation of flows on the planes of the wing at zero angle of attack and its "Fictitious body".
Looking at a strong increase in the “Fictitious body” in comparison with the original pushing front fairing, it becomes clear how surprisingly low frontal resistance is obtained in long spindly bodies, for example, in aircraft fuselage.
The streamlining of such forms reaches Cx = 0.06, whereas for a ball of the same section Cx = 0.4..0.5, and for a flat plate Cx = 1.
It turns out that in the discharge under the detachable jets in the frontal projection, resistance is not created at all. It remains only to land a detachable jet on a straight surface parallel to the velocity vector so that the impact does not produce a longitudinal to velocity component. With such a task perfectly cope long cylindrical fuselage with an elongated ovoid front fairing. It turns out that the frontal resistance of a huge fuselage is equal to the resistance of the ball at the tip of the tapering nose (see figure 19.)
The ratio of the diameter of the ball in the nose cone to the diameter of the fuselage depends on the speed of flight, and the higher the speed of flight, the narrower the nasal rounding becomes, pushing airflow apart. The increasing energy of the oncoming flow with a constant amount of frontal section requires scattering less and less air to the side of the fuselage while maintaining a constant section of the “fictitious body” behind the fairing. In supersonic, the radius of curvature of the nose fairing degenerates into the tip, but this is a completely different story.



Fig. 19. Wrap around the fuselage with detachable jets, under which creates a zone of zero resistance to flight. All the resistance of the fuselage is equal to the aerodynamic resistance of the ball in its nose fairing. And accompanying illustrations from textbooks on the topic of comparing resistance when air flows around various bodies.
Now consider the behavior of the detachable turbulent zones with a wing with a large angle of attack (see Figure 20).
First, it is necessary to trace the trajectory of the detachable flow above the stagnant zone until it meets with the flow from under the wing of the aircraft. Since the profile of the frontal fairing of the wing is considered symmetrical cylindrical, the detachable jets have equal power and trajectory, that is, they are also symmetric.
For the horizontal wing, we have already received a symmetrical two-sided separation bubble with the closure of jets on the wing in the same places.
When giving the wing a large angle of attack, the pattern of tear-off jets changes. At the same time, the dimensions of the “Separated bubbles” = “Stagnant zones” above and below the wing begin to differ dramatically in terms of volume.
As a result, as a “fictitious body,” a very swollen wing will be obtained with a significant flattening of the lower plane compared to the huge dome of the tear-off bubble on the upper wing plane. Interestingly, the equivalent virtual profile of the “fictitious body” at a large angle of attack of the wing with bloated detachable bubbles on the upper plane of the wing is surprisingly similar to the well-known EKIP aircraft. (see figure 21 )

Figure 20. The profile of the wing with the separation of flows on the planes of the wing at a high angle of attack and its "Fictitious body".



Fig.21. Ekranoplan EKIP. The layout of the perspective model of the Ekranoplan and the existing umenshchennaya model of the Ekranoplan (never taken off because of the project shutdown).
That is, in the EKIP Ekranolet, quite a sensible idea was offered to control the stagnant zone in the rear "shadow" part of the hull, which allowed the detachment jet to settle on the wing in the upper part of the dome, which gives greater lift force and reduces aerodynamic resistance to flight.
It turns out that the author of the EKIP was not such an inventor, offering such a hippo-like structure as an aircraft.
True, the EKIP should not fly very fast and at high angles of attack of the initial thin profile (about 15 degrees), with a correspondingly high frontal resistance.
The huge volume of cargo space in such a flying wing can more than compensate for some deterioration in aerodynamics. At the same time, a structurally planeless Aircraft-Wing looks much more attractive than a traditional aircraft with a separation of the functions of the thin “carrier wing” and “cargo-passenger fuselage”. That's just for a stable flight, you still have to add a long beam to accommodate the tail, as on the giant flying wing of the ANT-20 "Maxim Gorky."
A significant expansion of the wing (increase in the chord) makes the EKIP type aircraft also clearly pronounced the Ekranoplan in its aerodynamic properties when flying near the ground. So when flying on the screen, the “fictitious body” of the wing with a large angle of attack transforms into a strange iron, where the small nasal beak of the stagnation zone on the wing inflates to the size of a huge stagnant wedge under the wing (see figure 22).

Fig.22. The profile of the wing when flying above the screen at a large angle of attack and its "fictitious body".
Inside this sharp-nosed iron can be placed as profiles of EKIP and VBA-14 (Bartini) EKRANOLET, or a super-thick wing like ANT-20 “Maxim Gorky”.
Airplanes with a very thick wing were popular in the 1930s in the USSR, when the largest pre-war ANT-20 “Maxim Gorky” aircraft was created. This aircraft had a wing so thick and wide that several cabins were placed in the root compartments of the wing, where a person walked to his full height (see Fig. 16.).
True, this monster flew with a cruising speed of only 198km / h (maximum 220km / h).
If the ANT-20 slightly shortens the wing ends, leaving only the center of the thickest part, the plane will look like the later Ekranoplan "Caspian Monster" by Rostislav Alekseev.
It is interesting to compare similar in size “Maxim Gorky” from the 1930s with the “Caspian Monster” from the 60s (see table 5)
Tab.5. Comparative characteristics of the ANT-20 "Maxim Gorky" 1934. and Ekranoplan CM "Caspian Monster" 1966.

The table presents reference data that must be somehow interpreted.
Let's go first simple by direct comparison of homogeneous numbers by dividing each other.
Maximum weight: 544/42 = 13 times
Wing area: 662/486 = 1.36 times
Specific load on the wing: 13 / 1.36 = 9.5 times
Cruising speed:
430/198 = 2.17 times Difference of velocity head on cruising speed: 2.17 ^ 2 = 4.71 times
Power of power installations: (10 * 1300 * 9.81 * 430 / 3.6) / (8 * 900 000 * 0.735) = 28.8 times
Payload based on fuel: 304 / (42-28.5) = 22.51.
Practical range: 1500/1200 = 1.25
The ratio of fuel efficiency ANT-20 = 7150 / (1200 * 6) = 0.993 l / (t * km) The
gluttony of the CM is not known, but it can be estimated through power and speed.
When calculating the specific consumption for reference gluttony 0.8kg / (kgf * h) for the engine of the TRD VD-7.
The consumption of afterburner during acceleration from water is 10 * 13000 * 0.8 = 104 000 kg / h.
Considering the duration of a cruise flight on the screen with only two working engines out of ten available for acceleration and exit to the Screen, the economy will increase.
For a cruise flight with two engines 2 * 13 000 * 0.8 = 20 800 kg / h
Flight time 1500/430 = 3.5 hours
During the flight to the maximum range of 1500 km, the CM will eat at least 104 * 0.5 + 3.5 * 20.8 = 100 tons of fuel.
And the payload will be about 200 tons.
Fuel economy KM will get 100 000 / (1500 * 200) = 0.333 l / (t.km).
Conclusions from the obtained ratios:
1. According to the fuel efficiency, a CM can in the optimistic version turn out to be 3 times more economical than ANT-20.
Now the modern Airbus A380 airliner has a cargo modification A380F with the ability to carry cargo up to 150 tons at a distance of up to 10,370 km. The maximum take-off weight is 560 tons (the mass of the aircraft itself is 280 tons). The calculation of profitability for the cargo version of these indicators makes 130 tons of fuel 150 tons of cargo at a distance of 10370 km: 130000 / (150 * 10370) = 0.0835 l / (t * km).
In terms of passengers, the indicator is different: “Among large liners, the most economical is three liters of fuel per passenger per hundred kilometers (54 nautical miles). According to Airbus [5], the A380 burns 17% less fuel per passenger than the “modern largest aircraft” (apparently, the Boeing 747 is meant). “
That is, when checking for 850 passengers with luggage and seats, we will get an indicator close to the calculation for the cargo version.
It turns out that we not only began to fly 4-5 times faster over the past 80 years, but also improved fuel efficiency more than 10 times from the ANT-20 and 4 times from the Ekranoplan KM. Although only 20 years ago, our Airbus flew 5 times faster than ANT-25. The recent decline in speed in passenger aviation has been caused by the struggle for fuel-efficient flight.
2. The cruising speed of the CM is made so high by force, since at a lower speed it simply cannot fly on the screen. The flight condition on the screen is the fulfillment of the inequality “Velocity pressure”> “Average load on the wing”, that is,
Pv = 8560Pa at 430km / h (120m / s)> 544000 * 9.81 / 662.5 = 8055Pa.
3. The flight safety of a low-speed Giant Aircraft from the 30s is much better than that of an excessively high-speed WIG from the 60s, almost uncontrollably carried along among slow-moving ships and omnipresent water birds.
4. The cost of operating waterfree by sea ekranoplans is much more expensive than for land high-altitude aircraft. This is due to the excess number of engines needed only to start from the water and exit to the on-screen flight, as well as due to the extreme aggressiveness of the sea water when it affects the engines and the construction of the ground-effect vehicle when flying in clouds of splashes from nearby sea waves.
5. For the WGM KM it is easy to consider the quality of the wing when flying on two engines, equal to the ratio of their thrust to the weight of the wig itself K = 544 / (13 * 2) = 20.9. Thus, the aerodynamic efficiency of a large and heavy Ekranoplan is at the level of efficiency of the best modern large aircraft with a glider quality of the order of K = 18-20.
6. The three-fold gap in efficiency of the WGM Airbus 380F remains an enigma for me: Why, with the equal quality of the glider at the Airbus, fuel efficiency is 4 times better?
Or the whole secret lies in the terrible gluttony of the old Soviet turbojet engines in comparison with modern turbofan engines of a high degree of bypass ratio?
Bibliography:
- “Hydraulics and Aerodynamics”, Altshul AD, Moscow, Stroyizdat, 1986.-413с.
- "Aerodynamics" part 1, Krasnov NF, Moscow, Lenand, 2018, -496s.
- "Aerodynamics", Ed. Kalugina VT, Moscow, MGTU.N.E.Bauman, 2017, -607с.
