Walking experiments

A short story about how a simple physical model of walking, written almost on the knee, gave unexpectedly good results when compared with reality. For details I ask under a habrakat.

Model

First things first. The experiment was born out of interest to see if it is possible, when designing a walking mechanism, to achieve uniform and rectilinear movement of its body. The problem is pretty obvious. When moving the center of mass outside the foot, the force of gravity creates a moment tending to overturn the robot:

Of course, this can be avoided by increasing the feet. If their length is greater than the step width, then such instability does not occur. But such an exit is rather awkward. Fortunately, in addition to the supporting leg, we have a free leg, which can take on all the momentum of the momentum received by the mechanism and at the same time accelerate in the direction it needs. The model is to coordinate this movement of the free leg with the movement of the supporting leg and body. In this case, a condition arises on the maximum step length for given parameters of the robot and its speed, as well as the specific dynamics of the free leg.
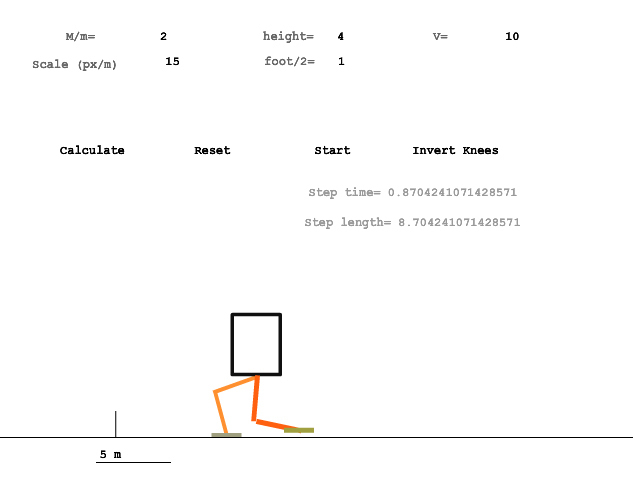
In order to see how the resulting movement would look, a small program was written.

Note: The model only considers plane motion. Therefore, the vertical vibrations of the body, caused by cross-over from leg to foot in the transverse direction, go beyond the boundaries of the subject.

Program

You can touch it here .

Legend: M / m is the ratio of the mass of the body to the mass of the legs, height is the height of the hip joint above the ground, foot is the length of the foot (half is set), v is the speed of the body, Scale is the scale of the picture.
All values ​​are in SI units.
After changing the input data, click Calculate to recalculate the model parameters.
A running vertical line is a person (for scale).

Results Analysis

For the sake of interest, I tried to take approximate parameters of a person as input and compare the data obtained by calculation with the experimental ones found on Wikipedia :

At that moment, the hairs on my head started to move a little. Of course, there are more real errors than a discrepancy in the graphs: the model is rather crude, and the “average person” is not an exact concept. But such a convergence cannot be clearly explained by pure chance either.

To also check the conclusions from the theory about the time dependence of the position of the feet, a video was selected for analysis . An ear cracked to determine the position of the body, and the approximate position of its middle was taken for the position of the foot. The results obtained for the reference and free phases of leg movement are presented on the graph:

(x is the coordinate along the axis directed along the direction of movement in the reference system associated with the body.)

In the model under consideration, the support foot moves uniformly relative to the body (because it is at rest relative to the ground, and the movement of the body relative to the ground is considered uniform). As you can see from the graph (blue line), in reality this is approximately what happens.

But much more interesting to consider the movement of the free leg. It follows from the model that its graph (red line) should consist of two pieces of cubic parabolas connected by a linearly dependent section:



After redrawing the data obtained in logarithmic coordinates, we get the following picture:


Red and blue colors indicate points that belong to different halves of the original red graph .

Points far from the origin are not of particular interest, since they relate to the area of ​​uniform motion. At the starting points, a straight line can be drawn, which indicates the presence of a power law dependence. The angular coefficient in this case is equal to ln (x) / ln (t) ≈tg (71⁰) ≈2.9. That is, the dependence, as follows from the theory, is close to cubic.

To summarize

The described model has no free parameters, except anthropological metrics and speed. However, this already turns out to be enough to calculate with good accuracy such general characteristics as the length and time of the step. And also in general terms describe the time dependence of the position of the feet.

I hope the material was interesting. Thank you for attention.