Krita: Four-Point Perspective Transformation

About a month ago, the Crete project successfully completed a fundraising campaign on Kickstarter (see last post ), now the developers are completely immersed in the process of writing the promised goodies. Four-point perspective transformations became the first realized goal. In this article I will talk about their implementation and application.

In general, “looking three-dimensional” transformations have existed in Crete for a long time, but it was inconvenient to use them. The fact is that the standard transformation tool allowed only to rotate the object around three axes. What is very poorly suited for the most popular user scenario: add texture to an object drawn with perspective in mind. The simplest example is to place windows on the walls of a building.

The easiest solution to this problem is to set the perspective on four points: select the window, drag its corners to the desired position and you're done! This method has been implemented.

Math conversion

As is known, a perspective transformation on a plane is defined by a transformation matrix of homogeneous coordinates.



This matrix consists of eight significant elements (scale-turns ( 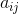), displacements ( 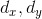), perspective ( 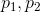)) and one scale factor. Thus, in order to uniquely specify the transformation, we need to have 8 equations relating these values. Four points, each with two coordinates, will precisely define these equations, provided that any three of them do not lie on one straight line.

Let there be four points (x1, y1) ... (x4, y4) in the coordinates of the original image. Express the fourth point through a linear combination of the first three:



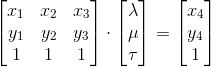
We solve the system and write the transformation matrix, which will translate (1,0,0) into a multiple (x1, y1,1), (0,1,0) into a multiple (x2, y2,1), (0,0,1 ) in (x3, y3,1) and (1,1,1) in (x4, y4,1)



Now we repeat these steps for the coordinates of the points in the finite space and get the matrix B in the hatched coordinates.



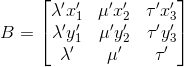
Then the desired transformation matrix will be of the form



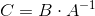
The matrix 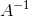will convert the original coordinates of the points to intermediate dummy points (1,0,0), (0,1,0), (0,0,1) and (1,1,1), and the matrix 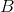, in turn, converts them to the desired values.

The desired matrix is ​​received!

Converting vanishing points

The vanishing point is the point at which parallel lines of an object converge in a perspective image. One of the requirements of the artists was the ability to drag these points directly. At first it was not entirely clear how to implement such a functional, but it soon became clear that vanishing points are expressed in homogeneous coordinates in an elementary way:



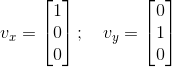
Further transformations do not change at all.

Instead of a conclusion

The described functionality is available in the latest builds of Krita for Windows and in the Krita Lime repositories for Ubuntu. You can update and draw!

Finally, a video from Pavel Geraskin demonstrating the capabilities of the new tool: