Implementation and testing of facial recognition algorithm

Content:

1. Search and analysis of the color space optimal for constructing prominent objects on a given class of images
2. Determination of the dominant signs of classification and the development of a mathematical model of facial expressions "
3. Synthesis of an optimal recognition algorithm for facial expressions
4. Implementation and testing of the facial recognition algorithm
5. Creation of a test database lip images of users in various states to increase the accuracy of the system
6. Search for the optimal audio speech recognition system based on open source passcode
7.Search for an optimal audio recognition system for speech recognition with closed source code, but with open APIs, for integration
8. Experiment of integrating a video extension into an audio recognition system with speech test protocol

Objectives:

Determine the most optimal algorithm for the recognition of facial expressions of a human face, consider ways of its implementation.

Tasks:

To analyze existing facial recognition algorithms, taking into account the dominant features of classification and the mathematical model that we have determined. Based on the data obtained, choose the optimal version of the algorithm for its subsequent implementation and testing.

Introduction

In previous scientific reports, a mathematical model for recognizing facial expressions was developed, and an algorithm for recognizing facial expressions was synthesized. There are two approaches to recognizing facial expressions - using a deformable model on the lip area and grabbing vector features of the lip area with their subsequent analysis using algorithms based on Gaussian mixtures. To implement facial recognition, you need to select the optimal algorithm.

1. Algorithms for recognizing a human face:

1.1 Algorithms based on a deformable model.

A deformable template model is a template of some shape (for a two-dimensional case, an open or closed curve, for a three-dimensional case, a surface). Superimposed on the image, the template is deformed under the influence of various forces, internal (specific for each specific template) and external (defined by the image on which the template is superimposed) - the model changes its shape, adapting to the input data [1]. The initial rough lip model is deformed under the action of force fields defined by the input image (Fig. 1).

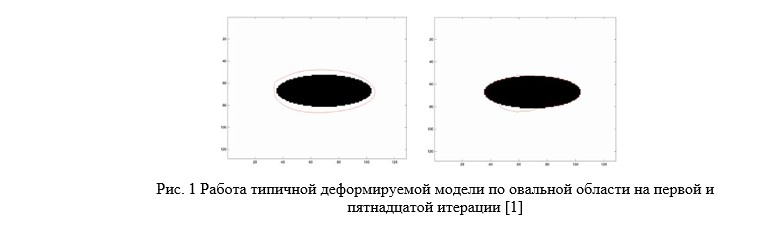
The main advantage over traditional search methods, such as the Hough transform [2], in which the search template is set rigidly, is that deformable models can change their shape during operation, allowing more flexible search for an object [3 ].

The main disadvantage of deformable models [4] is the need for a large number of iterations over a large number of frames, which significantly loads the system, but when the main calculations are carried out into the cloud, the system can be unloaded.

Deformable models can be classified according to the type of constraints imposed on their shape into two types: free-form deformable models and parametric deformable models.

1.1.1 Freeform deformable models

Freeform deformable models are deformable models that are subject to the general requirements of smoothness and continuity of the contour. An example of such a model is the snake [5]. The classic “snake” is a deformable model defined by a spline. The change in the deformable model is set by moving the spline control points along the image of the lips, the energy is set by the weighted sum of two components: the internal energy (set by the continuity and smoothness of the contour) and the external energy (set by the parts in the image to which the “snake” is attracted). The third term is also possible - additional energy, which sets additional user restrictions. "Snakes" are widely used in the processing of medical images [6], tasks of tracking movement, segmentation [7].

Formally, a “snake” is a parametric given contour c (s) = (x (s), y (s)). The energy of the “snake” is expressed by the sum ,
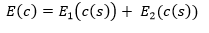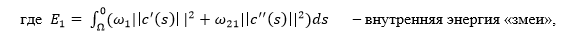
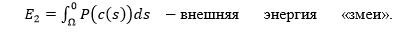Here P is the potential associated with the image and tightly connected with the lips. For a "snake" configured to search for borders, it is possible where I is the brightness of the image.

Minimizing energy, we obtain the desired parameters. Minimization can be carried out, for example, by the method of branches and borders. For this, the coordinates of each of the control points are iteratively sequentially changed; the change that led to the lowest energy value is used in the next iteration step. The minimization procedure ends when, at the next step, no change can reduce the energy of the “snake” (Fig. 2).

The main drawback of the “snake” is that if there are no pronounced details near the initializing position, the influence of internal energy, which determines the degree of smoothness of the desired object, tends to stretch the model excessively, degenerating it into a straight line, since the zero derivative (both the first and and second) direct minimizes the energy of the "snake". To avoid this effect, use a special kind of deformable models, the so-called balloon (ball) [8].

The main advantages of the “snake” include the relative ease of implementation (in the case of not including numerical optimization procedures) and resistance to variability of input data.

As a result, we can conclude that the use of a “snake” for recognizing facial expressions will entail the need to use numerical optimization methods, which will complicate an already cumbersome algorithm.

1.1.2 Parametric deformable models

Parametric deformable models are models that have more stringent shape constraints. The model is initialized with a strictly defined shape template, and with further deformations, the internal energy of the model controls its compliance with shape restrictions [9]. Such models have been widely used in the recognition of faces [10], gestures and human figures in images.

The equation of energy E of the snake, expressed by the formula v (s), looks like the usual "snake":

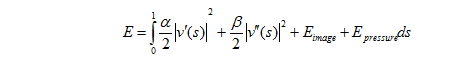
The first two terms describe the regularity energy of the snake. In our polar coordinate system, v (s) = [r (s), θ (s)], s is from 0 to 1. The third term is the energy related to the external force obtained from the image, the fourth with pressure.

External force is determined based on the above characteristics. She is able to shift the control points to a certain value of intensity. It is calculated as:

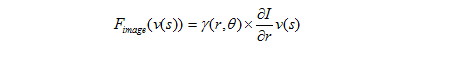
Analytically defined parametric deformable models are described by a set of primitives, in some way interconnected [10]. The primitives and the relationships between them participate in the calculation of internal energy, so that the shape of the deformable model cannot significantly deviate from the initializing form (Fig. 3).

Another variant of parametric deformable models is prototype based deformable models [9]. The initializing position and form of the prototype-based model is established by machine learning methods or high-level image processing.

The advantages of the parametric model over the “snake” are that in the general case there is no need for the use of restraining parameters, since the shape of the model varies within specified limits. Also, the need to use numerical optimization is often discarded. Based on experimental data [9], it works quite well.

The main disadvantage of the parametric model is the need to compose training samples, and the rebuilding of samples in case of changing model parameters.

As a result of comparing the “snake” and the parametrically specified model, it was concluded that the parametric model is the best choice, since changing the training samples is more comfortable than changing and adjusting the parameters for optimizing the results of the “snake”.

1.2 Algorithms based on Gaussian mixtures.

Gaussian mixtures are a set of distributions of a normal value [12]. A standard normal distribution is a normal distribution with a mathematical expectation of 0 and a standard deviation of 1. The sum of these quantities gives us a Gaussian mixture (Fig. 4).

The model of Gaussian mixtures is a weighted sum of M, components and can be written by the expression
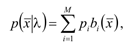(1)
where x is the D -dimensional vector of random variables; bi (x), i = 1, ..., M, are the distribution density functions of the components of the model and pi, i = 1, ..., M, are the weights of the model components. Each component is a D-dimensional Gaussian distribution function of the form
(2)
The complete model of a Gaussian mixture is determined by the mathematical expectation vectors, covariance matrices, and mixture weights for each component of the model. These parameters are collectively written in the form

In the facial recognition problem, each lip image is represented by a model of Gaussian mixtures and is put in accordance with its model λ. The Gaussian mixture model can take several different forms, depending on the type of covariance matrix.

The main advantage of using Gaussian mixtures is the intuitive assumption that the individual components of the model can simulate a certain set of acoustic signs / events [12].

The second advantage of using models of Gaussian mixtures to identify facial expressions is the empirical observation that a linear combination of Gaussian distributions can represent a large number of lip image classes. One of the strengths of the mix of Gaussian models is that these models can very accurately approximate arbitrary distributions.

The disadvantage of using the model of Gaussian mixtures lies in the difficulty of extracting the feature vector from each frame, as well as in the analysis of the data obtained, since it is difficult to divide them into classes.

Due to the complexity of the implementation and the large number of calculations, it is resource-consuming to use Gaussian mixtures in the recognition of facial expressions, and due to the ambiguity of the data obtained, it is difficult to get rid of the errors that arise.

Testing and conclusion:

This report examined facial recognition algorithms based on the properties of a deformable model (a deformable free-form model and a parametric model) and statistical characteristics (algorithms based on Gaussian mixtures). Deformable models are based on changes in the properties of the original template, and Gaussian mixtures involve the use of statistical characteristics of the region of interest.

The use of Gaussian mixtures involves processing a large amount of data [13], which is resource-consuming, and the use of a parametric deformable model requires pre-processing procedures that take at least 4 minutes of processor time [5]. That is why the choice fell on the use of the usual "snake", because it is most optimal in speed [3].

Fig. 5 Work of a deformable model according to a pre-binarized image of a person’s lips.

According to the studies, with preliminary binarization of the lip area, it is possible to significantly increase the quality of the active contour algorithm (Fig. 5). At the same time, it is possible to get rid of the procedures for pre-setting the system and analyzing reference images, as would be the case with the use of a parametric active model.

Confident determination of the contour of the lips will allow us to move on to the implementation of the task of direct analysis of micropauses, which will improve the existing audio speech recognition systems.

List of references

1) Demetri Terzopoulos, John Platt, Alan Barr, Kurt Fleischer. Elastically Deformable Models. Computer Graphics (Proceedings of ACM SIGGRAPH), Vol. 21, No. 4, pp. 205-214, July 1987.2
) Linda Shapiro, John Stockman. Computer vision. Moscow: Laboratory of Basic Knowledge, 2006.
3) Michael Kass, Andrew Witkin and Demetri Terzopoulos. Snakes: Active contour models. Int. Journal of Computer Vision, Vol. 1, No. 4, pp. 321-331, January 1988.4
) Shu-Fai Wong, Kwan-Yee Kenneth Wong. Robust Image Segmentation by Texture Sensitive Snake under Low Contrast Environment. In Proc. Int. Conference on Informatics in Control, Automation and Robotics, pp. 430-434, August 2004.
5) Michael Kass, Andrew Witkin and Demetri Terzopoulos. Snakes: Active contour models. Int. Journal of Computer Vision, Vol. 1, No. 4, pp. 321-331, January 1988.6
) Tim McInerney, Demetri Terzopoulos. Deformable Models in Medical Image Analysis: A Survey. Medical Image Analysis, 1 (2): pp. 91-108, 1996.
7) Doug P. Perrin, Christopher E. Smith. Rethinking Classical Internal Forces for Active Contour Models. Computer Vision and Pattern Recognition, Vol. 2, pp. 615-620, 2001.
8) Laurent D. Cohen. On Active Contour Models and Balloons. Computer Vision, Graphics and Image Processing: Image Understanding, Vol. 53, No. 2, pp. 211-218, March 1991.
9) Anil K. Jain, Yu Zhong, Sridan Lakshmanan. Object Matching Using Deformable Templates. IEEE Trans. on Pattern Anal. And Machine Intel. Vol. 18, No. 3, pp. 267-278, March 1996.
10) Alan L. Yuille, Peter W. Hallinan, David S. Cohen. Feature extraction from faces using deformable templates. Int. Journal of Computer Vision, Vol. 8, No. 2, pp. 99-111, August 1992.
11) Markel JD, Oshika BT, Gray AH // IEEE Trans. On Acoustics, Speech, and Signal Processing. 1977. Vol. 25. P. 330–337.
12) “Incremental Learning of Temporally-Coherent. Gaussian Mixture Models »Ognjen Arandjelovicґ, Roberto Cipolla, Department of Engineering, Cambridge.

To be continued