Looking for a melody by fragment
Greetings, dear readers of Habr!
In this article I want to tell how I searched for a piece of music.
So let's go!
The task before me is the following: there is a passage of a musical work, there is a base of musical works, and it is necessary to find which of the available musical works this passage belongs to.
Who cares, read under the harbokat.
I decided that for these purposes I will present music as a function of frequency versus time.
To do this, I will do the following:
I will “slice” the signal into the windows, as illustrated in the figure, and I will use a modification of the sliding window algorithm. The modification will consist in the fact that the window will not “glide smoothly” on the signal, but “move abruptly”, in other words, the windows will overlap.

As a window we take the so-called "Hamming window".
As the time instant of the appearance of the component with one or another frequency, we will take the time instant corresponding to the middle of the window. This modification will improve the resolution in the time and frequency domains: in the frequency domain due to the relatively large window, and in the time domain due to the fact that the Hamming window has a relatively narrow main lobe and when moving the window with an overlap, we can quite accurately record time samples.
In each window, we will perform the Fourier transform, in order to obtain the set of frequencies that are present in this window.
Total for an arbitrary composition, we get the following:
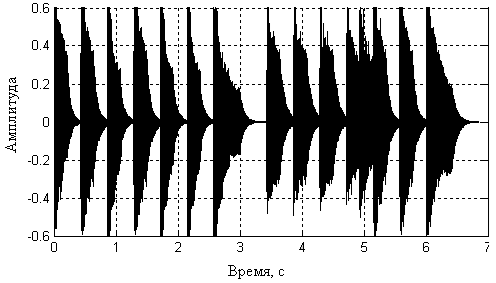
At the input - the dependence of the amplitude on time:
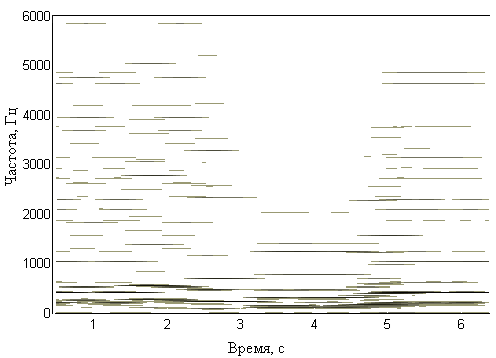
And at the output - the dependence of the amplitude on frequency:
This is not the end.
After we get the time-frequency representation, we filter out various interference and select frequencies that correspond to notes.
Thus, we get a time-note representation - a function of the note number versus time.
But here we are faced with the fact that the same melody can be played from different notes, for example (in figure (a) from a higher note, and in figure (b) from a lower note):
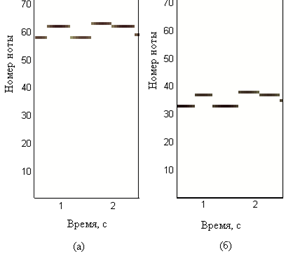
But if we look at the pictures, we will understand that the pictures are similar.
From here came the following idea: to identify a piece of music, regardless of the tonality on which it was played, one should take into account not the absolute values of the notes numbers and the time of their appearance, but relative ones - the differences between the values of the next and previous samples of notes numbers and times.
So, we can get a two-line matrix from the time-note function, in one line of which there will be differences of notes, and in the other line of the difference in the times of their appearance, so we will take into account the rhythm.
Despite the fact that the works were played on different keys, the following relationship is true:
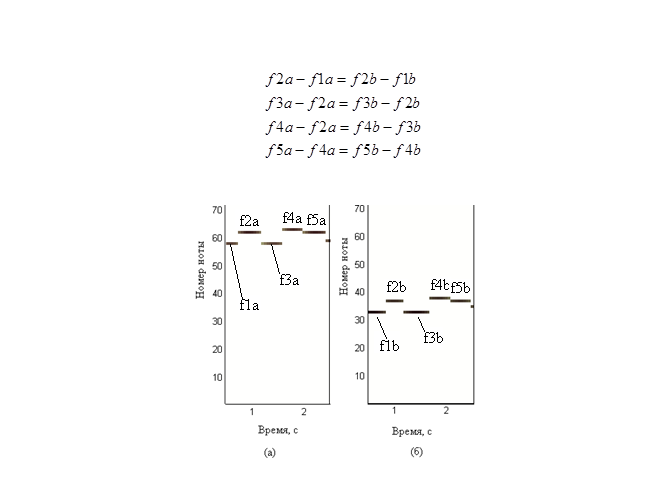
The identification algorithm is as follows:
And further, if the share of similarities in my case is above 75%, then, I believe that the melody is found.
In this article I want to tell how I searched for a piece of music.
So let's go!
The task before me is the following: there is a passage of a musical work, there is a base of musical works, and it is necessary to find which of the available musical works this passage belongs to.
Who cares, read under the harbokat.
I decided that for these purposes I will present music as a function of frequency versus time.
To do this, I will do the following:
I will “slice” the signal into the windows, as illustrated in the figure, and I will use a modification of the sliding window algorithm. The modification will consist in the fact that the window will not “glide smoothly” on the signal, but “move abruptly”, in other words, the windows will overlap.

As a window we take the so-called "Hamming window".
As the time instant of the appearance of the component with one or another frequency, we will take the time instant corresponding to the middle of the window. This modification will improve the resolution in the time and frequency domains: in the frequency domain due to the relatively large window, and in the time domain due to the fact that the Hamming window has a relatively narrow main lobe and when moving the window with an overlap, we can quite accurately record time samples.
In each window, we will perform the Fourier transform, in order to obtain the set of frequencies that are present in this window.
Total for an arbitrary composition, we get the following:
At the input - the dependence of the amplitude on time:

And at the output - the dependence of the amplitude on frequency:

This is not the end.
After we get the time-frequency representation, we filter out various interference and select frequencies that correspond to notes.
Thus, we get a time-note representation - a function of the note number versus time.
But here we are faced with the fact that the same melody can be played from different notes, for example (in figure (a) from a higher note, and in figure (b) from a lower note):

But if we look at the pictures, we will understand that the pictures are similar.
From here came the following idea: to identify a piece of music, regardless of the tonality on which it was played, one should take into account not the absolute values of the notes numbers and the time of their appearance, but relative ones - the differences between the values of the next and previous samples of notes numbers and times.
So, we can get a two-line matrix from the time-note function, in one line of which there will be differences of notes, and in the other line of the difference in the times of their appearance, so we will take into account the rhythm.
Despite the fact that the works were played on different keys, the following relationship is true:

The identification algorithm is as follows:
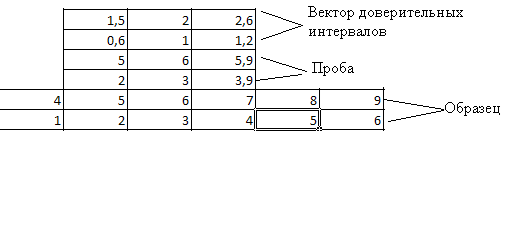
- vector of confidence intervals is calculated - an audio imprint of the signal accepted for the sample is taken (in this case, it is a matrix with two rows and a certain number of columns), and a vector of the same size is calculated, the elements of which are equal to thirty percent of the absolute values of the corresponding elements in the sample;
- then a smaller audio print is moved along a larger audio print according to the sliding window principle. In this case, the module of differences of the corresponding elements is considered, and verification is made so that this difference is no more than the corresponding elements of the vector of confidence intervals;

- if this difference is not greater, then the number of columns is considered. satisfying the condition;
- then this number is normalized by the number of columns in the "smaller" audio print;
- after that, the maximum share of similarity is selected.
And further, if the share of similarities in my case is above 75%, then, I believe that the melody is found.
