We help the robot sorter in the mail

Short background
I talked some time ago with a familiar robot. He settled temporarily at the Russian Post by a sorter of letters. The job is not dusty, it looks at the index on the letter and puts them in the desired hole. But there is a problem with letters that have a typo in the index. It takes a lot of time to figure out the correct index and the beer manages to run out of steam.
A splinter in the head
Enough time has passed since that conversation, but the dilemma of postal codes has not left my mind.
It would seem - what else can be improved here? Let’s try to transform the form of the digits of the index so that even if one error occurs, it can be automatically detected and corrected.
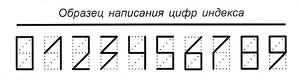
It turns out you can improve.
Let's try to draw a new kind of digit 0 .
If interested, why and why - I ask for a cat.
While still at the university, at a lecture on discrete mathematics, I noticed that the Hamming distance between some written numbers is too small, that is, they differ in just one wand. We will not go far for an example, these are 0 and 8. It is enough to “rearrange” one wand, and one digit turns into another.
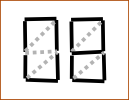
Further research
Are there still problems with similar numbers? Indeed, for this particular case, the greater the distance between the numbers, the easier it is for the robot to correct the error. We confine ourselves to one mistake in the figure. For example:

It can be seen that one stick is missing, however, algorithmically, you can determine what kind of error it was and fix it.
We will designate each stick of the skeleton of the digit with a number (yes, such a pun):
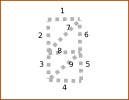
Assign each vector its own vector:
postindex[0]=[1,1,1,1,1,1,0,0,0];
postindex[1]=[0,0,0,0,1,1,1,0,0];
postindex[2]=[1,0,0,1,0,1,0,0,1];
postindex[3]=[1,0,0,0,0,0,1,1,1];
postindex[4]=[0,1,0,0,1,1,0,1,0];
postindex[5]=[1,1,0,1,1,0,0,1,0];
postindex[6]=[0,0,1,1,1,0,1,1,0];
postindex[7]=[1,0,1,0,0,0,1,0,0];
postindex[8]=[1,1,1,1,1,1,0,1,0];
postindex[9]=[1,1,0,0,0,1,0,1,1];
Now let's calculate the Hamming distance between the numbers:
0 1 2 3 4 5 6 7 8 9
'0': [ 0, 5, 4, 8, 4, 3, 5, 5, 1, 5 ]
'1': [ 5, 0, 5, 5, 3, 6, 4, 4, 6, 6 ]
'2': [ 4, 5, 0, 4, 6, 5, 7, 5, 5, 3 ]
'3': [ 8, 5, 4, 0, 6, 5, 5, 3, 7, 3 ]
'4': [ 4, 3, 6, 6, 0, 3, 5, 7, 3, 3 ]
'5': [ 3, 6, 5, 5, 3, 0, 4, 6, 2, 4 ]
'6': [ 5, 4, 7, 5, 5, 4, 0, 4, 4, 8 ]
'7': [ 5, 4, 5, 3, 7, 6, 4, 0, 6, 6 ]
'8': [ 1, 6, 5, 7, 3, 2, 4, 6, 0, 4 ]
'9': [ 5, 6, 3, 3, 3, 4, 8, 6, 4, 0 ]Code for Unbelievers
var postindex = {};
postindex[0]=[1,1,1,1,1,1,0,0,0];
postindex[1]=[0,0,0,0,1,1,1,0,0];
postindex[2]=[1,0,0,1,0,1,0,0,1];
postindex[3]=[1,0,0,0,0,0,1,1,1];
postindex[4]=[0,1,0,0,1,1,0,1,0];
postindex[5]=[1,1,0,1,1,0,0,1,0];
postindex[6]=[0,0,1,1,1,0,1,1,0];
postindex[7]=[1,0,1,0,0,0,1,0,0];
postindex[8]=[1,1,1,1,1,1,0,1,0];
postindex[9]=[1,1,0,0,0,1,0,1,1];
function Hamming_distance(a, b) {
var sum = 0;
for (var i = 0; i < a.length; i++) {
sum += Math.abs(a[i]-b[i]);
}
return sum;
}
console.log(postindex);
var hd = {};
for (var i = 0; i < 10; i++) {
var arr = [];
for (var j = 0; j < 10; j++) {
arr[j] = Hamming_distance(postindex[i],postindex[j]);
hd[i] = arr;
}
}
console.log('');
console.log(hd);
It can be seen that the problem between 0 and 8 is the largest (the distance is only 1 unit), there is still a problem between 5 and 8 , there is a distance of 2, which is also not very good, especially for such a typo:
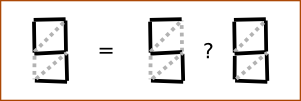
This is an irregularly shaped nine, changing only one wand, can turn into 8 and 5 . (We don’t consider the fact that the figure is similar to another 9, because 2 errors are needed there)
What can be done?
Let's try to start by changing the number 0 .
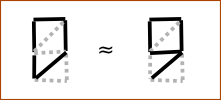
Too similar to 9 . There will be the same problem as 5 and 8 .
Another option:
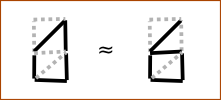
Similar to 6 .
Tilt Zero:
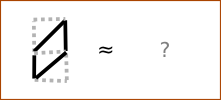
It seems to be what you need. We check:
0 1 2 3 4 5 6 7 8 9
'0': [ 0, 3, 4, 4, 6, 9, 5, 3, 7, 5 ]
'1': [ 3, 0, 5, 5, 3, 6, 4, 4, 6, 6 ]
'2': [ 4, 5, 0, 4, 6, 5, 7, 5, 5, 3 ]
'3': [ 4, 5, 4, 0, 6, 5, 5, 3, 7, 3 ]
'4': [ 6, 3, 6, 6, 0, 3, 5, 7, 3, 3 ]
'5': [ 9, 6, 5, 5, 3, 0, 4, 6, 2, 4 ]
'6': [ 5, 4, 7, 5, 5, 4, 0, 4, 4, 8 ]
'7': [ 3, 4, 5, 3, 7, 6, 4, 0, 6, 6 ]
'8': [ 7, 6, 5, 7, 3, 2, 4, 6, 0, 4 ]
'9': [ 5, 6, 3, 3, 3, 4, 8, 6, 4, 0 ]
Everything is very good! We figured out one of the numbers.
Fight to the end
Now you need to come up with something for 5 and 8 . Say NO to a Hamming distance of less than three. We draw fives of varying degrees of ugliness.
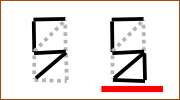
For the second option, the minimum Hamming distance for all numbers is more than two, but this ugliness can hardly be called five. We think about other options.
Maybe you should use the fully shaded version as the figure eight?

Testing:
0 1 2 3 4 5 6 7 8 9
'0': [ 0, 3, 4, 4, 6, 9, 5, 3, 5, 5 ]
'1': [ 3, 0, 5, 5, 3, 6, 4, 4, 6, 6 ]
'2': [ 4, 5, 0, 4, 6, 5, 7, 5, 5, 3 ]
'3': [ 4, 5, 4, 0, 6, 5, 5, 3, 5, 3 ]
'4': [ 6, 3, 6, 6, 0, 3, 5, 7, 5, 3 ]
'5': [ 9, 6, 5, 5, 3, 0, 4, 6, 4, 4 ]
'6': [ 5, 4, 7, 5, 5, 4, 0, 4, 4, 8 ]
'7': [ 3, 4, 5, 3, 7, 6, 4, 0, 6, 6 ]
'8': [ 5, 6, 5, 5, 5, 4, 4, 6, 0, 4 ]
'9': [ 5, 6, 3, 3, 3, 4, 8, 6, 4, 0 ]
Hurrah! There are no deuces in the matrix
Final option

In this scheme of numbers, one any mistake made can be automatically corrected.
Epilogue
The result of my thoughts of a familiar robot satisfied, but he expressed fears that everyone would not be able to immediately get used to this option. But I assured him that this change was necessary for the benefit of the Russians. Letters will reach faster and there will be fewer errors. And if people still don’t like this option of writing index numbers, then we will return the old scheme. In general, we win anyway.
UPD:
Habrauser jaguard proposed a more elegant solution to the problem.
