Work with geolocations in highload mode
When developing software, interesting tasks often arise. One of these: working with geo-coordinates of users. If millions of users use your service and requests to RDBMSs often occur, then the choice of algorithm plays an important role. About how to optimally handle a large number of requests and look for the next geo-position described under the cat.
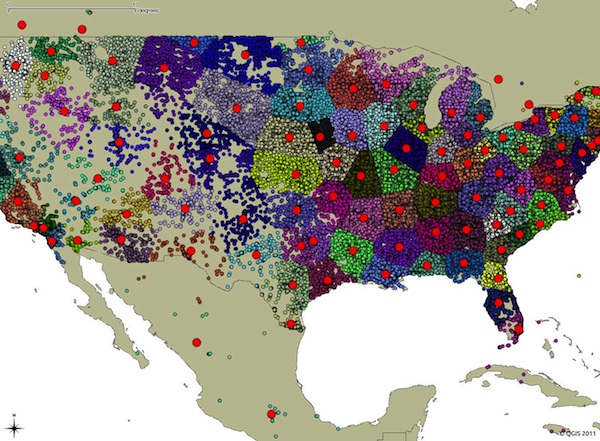
In the process of developing the Pushwoosh push notification service , a fairly well-known task arose. There are many geofences. The geofence is set by geographic coordinates. When a user passes by one of such geofences (for example, a snack bar), he should receive a push notification (“Yo, come to us and sign up with a 20% discount). For simplicity, we assume that the radius of all geofences is the same. In conditions of a large number of geofences and a large number of users (we have 500 million!) Who are constantly moving, the search for the nearest geofence should be carried out as quickly as possible. In English literature, this task is known as Nearest neighbor search.. At first glance, it seems that in order to solve this problem, it is necessary to calculate the distance from the user to each geofence and the complexity of this algorithm is linear O (n), where n is the number of geofences. But let's solve this problem in the logarithm of O (log n)!
Let's start with the simple - latitude and longitude. To indicate the position of a point on the surface of the Earth, you can use:
It is necessary to pay attention that x is longitude, y is latitude (Google Maps, Yandex.Maps and all other services indicate the longitude of the first).
Geographic coordinates can be translated into spatial - just a point (x, y, z). Anyone interested in more details can see Wikipedia .
The number of decimal places determines the accuracy:
If accuracy up to one meter is needed, then 5 decimal places should be stored.
Suppose we have a service that is used by millions of people, and we want to store their geographical coordinates. The obvious approach in this case is to enter two fields in the table - latitude / longitude. You can use double precision (float8), which takes up 8 bytes. As a result, we need 16 bytes to store the coordinates of one user.
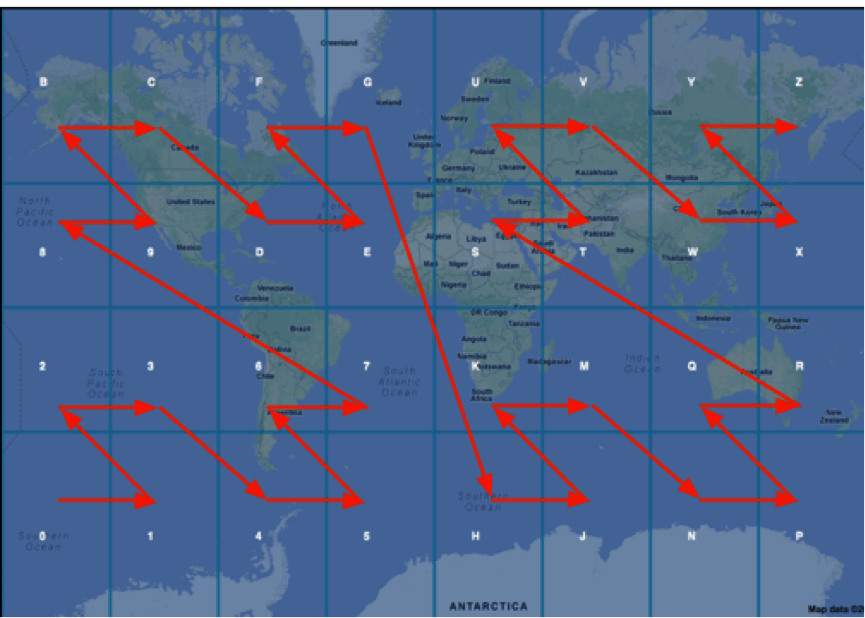
But there is another approach called geohashing . The idea is simple. Latitude and longitude are encoded into a number, which is then encoded in base-32. The map is divided into a 4x8 matrix and each cell is assigned a symbol (alphanumeric).
To increase accuracy, each cell is divided into smaller ones, while characters are added to the code (to be exact, numbers, and after that there is encoding in base-32).
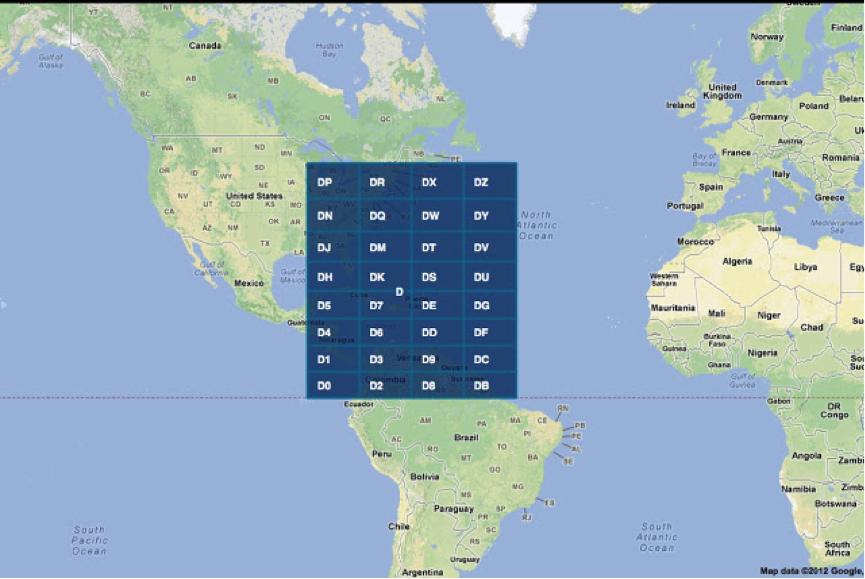
Partitioning can be done to the required accuracy. Such a code is unique for each point.
I won’t describe the construction algorithm in detail; you can read about it on Wikipedia . His idea is similar to arithmetic coding . This code is reversible. Many technologies already have built-in methods for working with geo-hashes, for example, MongoDB .
Example: coordinates 57.64911,10.40744 will be encoded in u4pruydqqvj (11 characters). If less accuracy is required, then the code will be less.
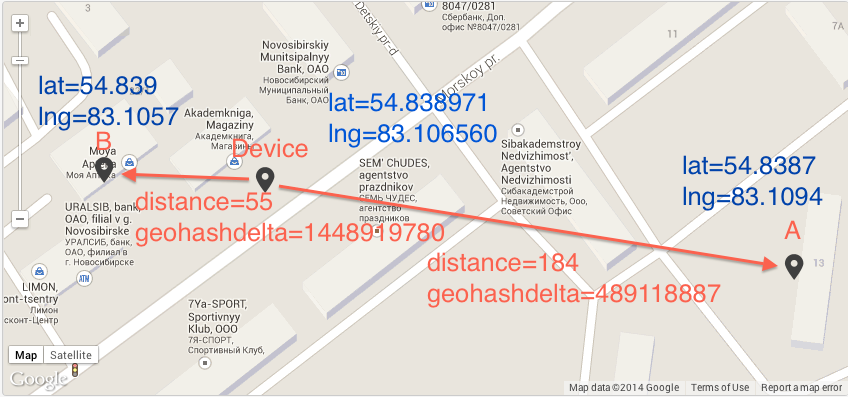
The peculiarity of this code is that NORMALLY nearby points have the same prefix. And you can calculate the difference between geo-hashes to determine the proximity of two points. But unfortunately this algorithm is not accurate, this can be clearly seen from the previous images. Cells with codes 7 and 8 are farther apart than cells 2 and 8.
As an example, I’ll give a picture where the geo-hash gives the wrong result (geohashdelta - the difference between geocheses without base32)
If you can neglect the accuracy of the task, you can create geohash field in the table, add an index on it and search for the logarithm.
You can write a stored procedure
and use her
But in the end there will be a Seq Scan, which is not very pleasant.
What to do when accuracy cannot be neglected? There is already a special Kd tree data structure for this . You can translate the latitude and longitude into (x, y, z) build a tree on them and search the tree on average for the logarithm.
PostGIS is an extension that significantly extends the processing of geographic features in PostgreSQL RDBMS.
To solve our problem, we will use the three-dimensional coordinate system SRID 4326 ( WGS 84 ). This coordinate system determines the coordinates relative to the center of mass of the Earth, the error is less than 2 cm.
If you have an ubuntu-like system, then PostGIS can be installed from the package (for PostgreSQL 9.1):
And connect the necessary extensions:
Using \ dx, you can see all installed extensions.
Create an index relation for the location field
Then, to search for the nearest geofence, you can use the following query
Here <-> is the distance operator. We calculated the distance and found the next 10 geofences!
STOP, you say! After all, this query should look at all the records in the table and calculate the distance to each geofence O (n).
Let's see the EXPLAIN ANALYZE request
Index Scan! Where is the magic?
And she is in the GiST index.
PostgreSQL supports 3 types of indexes:
The GiST index implemented by PostGIS supports distance operator <-> when searching. Also, this index can be composite!
This functionality can be implemented without using PostGIS, using the btree-gist index , but PostGIS provides convenient methods for translating latitude and longitude into WGS 84.
[1] Interesting examples of requests from postgresql.ru.net/postgis/ch04_6.html
[2] Admiration for ease of use boundlessgeo.com/2011/09/indexed-nearest-neighbour-search-in-postgis
[3] Presentation that this approach can be used not only for latitude / longitude, but also for streets and other interesting objects www.hagander.net/talks/Find%20your%20neighbours.pdf
[4] Presentation of KNN developers GIst-index www.sai.msu.su /~megera/postgres/talks/pgcon-2010-1.pdf
PS
Postgres version> = 9.1
PostGIS version> = 2.0

Nearest Neighbor Search Task
In the process of developing the Pushwoosh push notification service , a fairly well-known task arose. There are many geofences. The geofence is set by geographic coordinates. When a user passes by one of such geofences (for example, a snack bar), he should receive a push notification (“Yo, come to us and sign up with a 20% discount). For simplicity, we assume that the radius of all geofences is the same. In conditions of a large number of geofences and a large number of users (we have 500 million!) Who are constantly moving, the search for the nearest geofence should be carried out as quickly as possible. In English literature, this task is known as Nearest neighbor search.. At first glance, it seems that in order to solve this problem, it is necessary to calculate the distance from the user to each geofence and the complexity of this algorithm is linear O (n), where n is the number of geofences. But let's solve this problem in the logarithm of O (log n)!
Geographical coordinates
Let's start with the simple - latitude and longitude. To indicate the position of a point on the surface of the Earth, you can use:
- Latitude - goes from north to south. 0 is the equator. Varies from -90 to 90 degrees.
- Longitude (longitude) - goes from west to east. 0 - zero meridian (Greenwich). It varies from -180 to 180 degrees.
It is necessary to pay attention that x is longitude, y is latitude (Google Maps, Yandex.Maps and all other services indicate the longitude of the first).
Geographic coordinates can be translated into spatial - just a point (x, y, z). Anyone interested in more details can see Wikipedia .
The number of decimal places determines the accuracy:
| Degrees | Distance |
|---|---|
| 1 | 111 km |
| 0.1 | 11.1 km |
| 0.01 | 1.11 km |
| 0.001 | 111 m |
| 0.0001 | 11.1 m |
| 0.00001 | 1.11 m |
| 0.000001 | 11.1 cm |
If accuracy up to one meter is needed, then 5 decimal places should be stored.
Geohashing
Suppose we have a service that is used by millions of people, and we want to store their geographical coordinates. The obvious approach in this case is to enter two fields in the table - latitude / longitude. You can use double precision (float8), which takes up 8 bytes. As a result, we need 16 bytes to store the coordinates of one user.
But there is another approach called geohashing . The idea is simple. Latitude and longitude are encoded into a number, which is then encoded in base-32. The map is divided into a 4x8 matrix and each cell is assigned a symbol (alphanumeric).

To increase accuracy, each cell is divided into smaller ones, while characters are added to the code (to be exact, numbers, and after that there is encoding in base-32).

Partitioning can be done to the required accuracy. Such a code is unique for each point.
I won’t describe the construction algorithm in detail; you can read about it on Wikipedia . His idea is similar to arithmetic coding . This code is reversible. Many technologies already have built-in methods for working with geo-hashes, for example, MongoDB .
Example: coordinates 57.64911,10.40744 will be encoded in u4pruydqqvj (11 characters). If less accuracy is required, then the code will be less.
The peculiarity of this code is that NORMALLY nearby points have the same prefix. And you can calculate the difference between geo-hashes to determine the proximity of two points. But unfortunately this algorithm is not accurate, this can be clearly seen from the previous images. Cells with codes 7 and 8 are farther apart than cells 2 and 8.
As an example, I’ll give a picture where the geo-hash gives the wrong result (geohashdelta - the difference between geocheses without base32)

If you can neglect the accuracy of the task, you can create geohash field in the table, add an index on it and search for the logarithm.
Full search
You can write a stored procedure
create or replace function gc_dist(_lat1 float8, _lon1 float8, _lat2 float8, _lon2 float8) returns float8 as
$$
DECLARE
radian CONSTANT float8 := PI()/360;
BEGIN
return ACOS(SIN($1*radian) * SIN($3*radian) + COS($1*radian) * COS($3*radian) * COS($4*radian-$2*radian)) * 6371;
END;
$$ LANGUAGE plpgsql;
and use her
explain SELECT *, gc_dist(54.838971, 83.106560, lat, lng) AS pdist FROM geozones WHERE applicationid = 3890 ORDER BY pdist ASC LIMIT 10;
But in the end there will be a Seq Scan, which is not very pleasant.
Limit (cost=634.72..634.75 rows=10 width=69)
-> Sort (cost=634.72..639.72 rows=2001 width=69)
Sort Key: (gc_dist(54.838971::double precision, 83.10656::double precision, (lat)::double precision, (lng)::double precision))
-> Seq Scan on geozones (cost=0.00..591.48 rows=2001 width=69)
Kd tree and R tree
What to do when accuracy cannot be neglected? There is already a special Kd tree data structure for this . You can translate the latitude and longitude into (x, y, z) build a tree on them and search the tree on average for the logarithm.
Postgis
PostGIS is an extension that significantly extends the processing of geographic features in PostgreSQL RDBMS.
To solve our problem, we will use the three-dimensional coordinate system SRID 4326 ( WGS 84 ). This coordinate system determines the coordinates relative to the center of mass of the Earth, the error is less than 2 cm.
If you have an ubuntu-like system, then PostGIS can be installed from the package (for PostgreSQL 9.1):
sudo apt-get install python-software-properties;
sudo apt-add-repository ppa:ubuntugis/ppa;
sudo apt-get update;
sudo apt-get install postgresql-9.1-postgis;
And connect the necessary extensions:
CREATE EXTENSION postgis;
CREATE EXTENSION btree_gist; -- for GIST compound index
Using \ dx, you can see all installed extensions.
Create an index relation for the location field
CREATE TABLE geozones_test (
uid SERIAL PRIMARY KEY,
lat DOUBLE PRECISION NOT NULL CHECK(lat > -90 and lat <= 90),
lng DOUBLE PRECISION NOT NULL CHECK(lng > -180 and lng <= 180),
location GEOMETRY(POINT, 4326) NOT NULL -- PostGIS geom field with SRID 4326
);
CREATE INDEX geozones_test_location_idx ON geozones_test USING GIST(location);
Then, to search for the nearest geofence, you can use the following query
SELECT *, ST_Distance(location::geography, 'SRID=4326;POINT(83.106560 54.838971)'::geography)/1000 as dist_km
FROM geozones_test ORDER BY location <-> 'SRID=4326;POINT(83.106560 54.838971)' limit 10;
Here <-> is the distance operator. We calculated the distance and found the next 10 geofences!
STOP, you say! After all, this query should look at all the records in the table and calculate the distance to each geofence O (n).
Let's see the EXPLAIN ANALYZE request
EXPLAIN ANALYZE
SELECT *, ST_Distance(location::geography, 'SRID=4326;POINT(83.106560 54.838971)'::geography)/1000 as dist_km
FROM geozones_test ORDER BY location <-> 'SRID=4326;POINT(83.106560 54.838971)' limit 10;
Limit (cost=0.00..40.36 rows=10 width=227) (actual time=0.236..0.510 rows=10 loops=1)
-> Index Scan using geozones_test_location_idx on geozones_test (cost=0.00..43460.37 rows=10768 width=227) (actual time=0.235..0.506 rows=10 loops=1)
Order By: (location <-> '0101000020E6100000F4C308E1D1C654406EA5D766636B4B40'::geometry)
Total runtime: 0.579 ms
Index Scan! Where is the magic?
And she is in the GiST index.
PostgreSQL supports 3 types of indexes:
- B-Tree - used when data can be sorted along one axis; e.g. numbers, characters, dates. GIS data cannot be sorted along a single axis in a rational way (which is greater: (0,0) or (0,1) or (1,0)?), And therefore B-Tree will not help to index them. B-Tree work with operators <, <=, =,> =,>, etc.
- Hash - can only work with equality comparison. Also, this index is not Write-Ahead logging - that is, an index from backup may not rise.
- GIN indexes are "inverted" indexes that can handle values containing more than one key, such as arrays.
- GiST indexes (Generalized Search Trees) are a kind of infrastructure in which many different indexing strategies can be implemented. GiST indexes divide data into objects on one side (things to one side), intersecting objects (things which overlap), objects inside (things which are inside) and can be used for many types of data, including GIS data.
The GiST index implemented by PostGIS supports distance operator <-> when searching. Also, this index can be composite!
This functionality can be implemented without using PostGIS, using the btree-gist index , but PostGIS provides convenient methods for translating latitude and longitude into WGS 84.
References:
[1] Interesting examples of requests from postgresql.ru.net/postgis/ch04_6.html
[2] Admiration for ease of use boundlessgeo.com/2011/09/indexed-nearest-neighbour-search-in-postgis
[3] Presentation that this approach can be used not only for latitude / longitude, but also for streets and other interesting objects www.hagander.net/talks/Find%20your%20neighbours.pdf
[4] Presentation of KNN developers GIst-index www.sai.msu.su /~megera/postgres/talks/pgcon-2010-1.pdf
PS
Postgres version> = 9.1
PostGIS version> = 2.0
Only registered users can participate in the survey. Please come in.
Rate the usefulness of the article
- 62.1% I learned a lot. 204
- 27.7% I learned a little new 91
- 10% I did not learn anything new from this article 33
