Consensus in distributed systems. Paxos
Recently, scientific publications increasingly mention the consensus algorithm in distributed systems called Paxos. Among such publications, a number of works by Google employees ( Chubby , Megastore , Spanner ) previously partially covered on the hub , the architecture of WANdisco , Ceph systems , etc. At the same time, the Paxos algorithm itself is considered difficult to understand , although it is based on elementary principles.
In this article I will try to correct this situation and tell about this algorithm in a clear language, as the author of the algorithm, Leslie Lamport, once tried to make it .
First you need to understand the problem that this algorithm solves. To do this, imagine a distributed information processing system, which is a cluster of x86 servers. If for one server the probability of failure is small and often when implementing simple systems it can be neglected, then for a cluster of servers the probability of failure of one of the servers becomes several times greater: MTBF for one of N servers is N times less than MTBF for one server. Add to this the network unreliability in the form of network equipment failure and packet loss, hard drive failures, server software failures at the OS and application level. According to google, then for a cluster of 1800 machines they talk about 1000 server failures during the first year of operation of the cluster, that is, 3 failures per day - and this is not counting hard drive failures, network and power problems, etc. As a result, if you do not lay fault tolerance in the software of a distributed system, we will get a system in which each of the above problems leads to a system failure.
Therefore, the task of reaching consensus is the task of obtaining an agreed value by a group of participants in a situation where individual participants may fail, providing incorrect information, distorting the transmitted values by the data transmission medium. In general, scenarios of abnormal functioning of components of distributed systems can be divided into two classes:
Second-class errors are much more difficult to detect and correct. In general, Leslie Lamport proved that in order to correct the Byzantine problem in N nodes, a distributed system should consist of at least 3N + 1 nodes and should implement a special consensus algorithm. Fault tolerance at this level is required for the most part in systems whose criticality is extremely high (for example, in the tasks of the space industry).
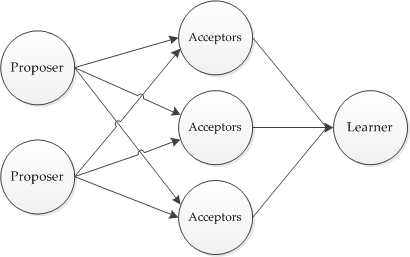
In cluster computing, fault tolerance is usually understood as the system's resistance to complete component failures. To achieve consensus in such systems, the Paxos algorithm is used. An algorithm has been proposedLeslie Lamport in the 90s of the last century and named after the Greek island of Paxos with a fictional system of organizing the work of parliament. To achieve consensus, this algorithm requires that at least N + 1 nodes function in a system of 2N + 1 nodes , these N + 1 nodes are called “quorum”. The essence of the algorithm in the interaction of agents with the following roles:
The basic Paxos algorithm consists of the following steps:
1a. Prepare ("offer"). In this phase, the proposer generates a “sentence” with sequence number N and sends it to all acceptor. For each of the following “proposals”, the number N must be greater than the one selected previously
1b. Promise ("promise"). Each acceptor receives an "offer" to the sequence number N and the value of V . If the number of "offers" more than all the acceptor data received previously, he must respond to this message "promise" not to take more than "proposals" with a serial number less of N . If the given acceptor has already accepted any “offer”, it must return the number Ni of this “sentence” and the accepted value V i , otherwise it returns an empty value
2a. Accept! ("to accept"). If a proposer has received “promises” from the acceptor quorum, it considers the request ready for further processing. In the event that with the “promises” from the acceptor the values N i and V i also come, proposer chooses V equal to the value V i of the “promise” with the maximum N i . Then the proposer sends a “accept” request to all acceptor, which contains the values of N and V
2b. Accepted("accepted"). When the acceptor receives the message "accept" with the values of N and the V , he takes it only when previously he had not "promised" to make proposals with numbers strictly greater than N . Otherwise, it takes a value and responds with a “accepted” message to all learner.
The learner task is simple - to receive a “accepted” message with a value of V and remember it.
Example of an algorithm:
What happens if any of the components of a distributed system fails?
Failure Acceptor:
Learner Failures:
Failure Proposer:
In the event of a proposer failure, the system must select a new proposer, usually by voting after a timeout has elapsed waiting for the old proposer to return. In the event that after choosing a new proposer, the old one comes back to life, a conflict may arise between the leaders, which can lead to a loop of the system:
As an example of implementation, I will give a slightly modified python code of one of the github repositories :
Literature:

In this article I will try to correct this situation and tell about this algorithm in a clear language, as the author of the algorithm, Leslie Lamport, once tried to make it .
First you need to understand the problem that this algorithm solves. To do this, imagine a distributed information processing system, which is a cluster of x86 servers. If for one server the probability of failure is small and often when implementing simple systems it can be neglected, then for a cluster of servers the probability of failure of one of the servers becomes several times greater: MTBF for one of N servers is N times less than MTBF for one server. Add to this the network unreliability in the form of network equipment failure and packet loss, hard drive failures, server software failures at the OS and application level. According to google, then for a cluster of 1800 machines they talk about 1000 server failures during the first year of operation of the cluster, that is, 3 failures per day - and this is not counting hard drive failures, network and power problems, etc. As a result, if you do not lay fault tolerance in the software of a distributed system, we will get a system in which each of the above problems leads to a system failure.
Therefore, the task of reaching consensus is the task of obtaining an agreed value by a group of participants in a situation where individual participants may fail, providing incorrect information, distorting the transmitted values by the data transmission medium. In general, scenarios of abnormal functioning of components of distributed systems can be divided into two classes:
- Complete component failure. This class of problems is characterized by the fact that such a failure leads to the inaccessibility of one of the components of the distributed system (or network segmentation, in the event of a switch failure). This class of problems includes: server failure, storage system failure, switch failure, operating system failure, application failure;
- Byzantine mistake. It is characterized by the fact that the system node continues to function, but at the same time can return incorrect information. Suppose, when using RAM without ECC, it can lead to reading incorrect data from memory, errors in network equipment can lead to packet corruption, etc.
Second-class errors are much more difficult to detect and correct. In general, Leslie Lamport proved that in order to correct the Byzantine problem in N nodes, a distributed system should consist of at least 3N + 1 nodes and should implement a special consensus algorithm. Fault tolerance at this level is required for the most part in systems whose criticality is extremely high (for example, in the tasks of the space industry).
In cluster computing, fault tolerance is usually understood as the system's resistance to complete component failures. To achieve consensus in such systems, the Paxos algorithm is used. An algorithm has been proposedLeslie Lamport in the 90s of the last century and named after the Greek island of Paxos with a fictional system of organizing the work of parliament. To achieve consensus, this algorithm requires that at least N + 1 nodes function in a system of 2N + 1 nodes , these N + 1 nodes are called “quorum”. The essence of the algorithm in the interaction of agents with the following roles:
- Client - a client of a distributed system that can send a request and receive a response to it
- Proposer - a component of a distributed system responsible for organizing the voting process
- Acceptor - a component of a distributed system that has the right to vote for the acceptance or rejection of a specific proposal from Proposer
- Learner - a component of the system that remembers the decision
The basic Paxos algorithm consists of the following steps:
1a. Prepare ("offer"). In this phase, the proposer generates a “sentence” with sequence number N and sends it to all acceptor. For each of the following “proposals”, the number N must be greater than the one selected previously
1b. Promise ("promise"). Each acceptor receives an "offer" to the sequence number N and the value of V . If the number of "offers" more than all the acceptor data received previously, he must respond to this message "promise" not to take more than "proposals" with a serial number less of N . If the given acceptor has already accepted any “offer”, it must return the number Ni of this “sentence” and the accepted value V i , otherwise it returns an empty value
2a. Accept! ("to accept"). If a proposer has received “promises” from the acceptor quorum, it considers the request ready for further processing. In the event that with the “promises” from the acceptor the values N i and V i also come, proposer chooses V equal to the value V i of the “promise” with the maximum N i . Then the proposer sends a “accept” request to all acceptor, which contains the values of N and V
2b. Accepted("accepted"). When the acceptor receives the message "accept" with the values of N and the V , he takes it only when previously he had not "promised" to make proposals with numbers strictly greater than N . Otherwise, it takes a value and responds with a “accepted” message to all learner.
The learner task is simple - to receive a “accepted” message with a value of V and remember it.
Example of an algorithm:
Client Proposer Acceptor Learner
| | | | | | |
X-------->| | | | | | Request
| X--------->|->|->| | | Prepare(1)
| |<---------X--X--X | | Promise(1,{Va,Vb,Vc})
| X--------->|->|->| | | Accept!(1,Vn=last(Va,Vb,Vc))
| |<---------X--X--X------>|->| Accepted(1,Vn)
|<---------------------------------X--X Response
| | | | | | |
What happens if any of the components of a distributed system fails?
Failure Acceptor:
Client Proposer Acceptor Learner
| | | | | | |
X-------->| | | | | | Request
| X--------->|->|->| | | Prepare(1)
| | | | ! | | !! FAIL !!
| |<---------X--X | | Promise(1,{null,null, null})
| X--------->|->| | | Accept!(1,V)
| |<---------X--X--------->|->| Accepted(1,V)
|<---------------------------------X--X Response
| | | | | |
Learner Failures:
Client Proposer Acceptor Learner
| | | | | | |
X-------->| | | | | | Request
| X--------->|->|->| | | Prepare(1)
| |<---------X--X--X | | Promise(1,{null,null,null})
| X--------->|->|->| | | Accept!(1,V)
| |<---------X--X--X------>|->| Accepted(1,V)
| | | | | | ! !! FAIL !!
|<---------------------------------X Response
| | | | | |
Failure Proposer:
Client Proposer Acceptor Learner
| | | | | | |
X----->| | | | | | Request
| X------------>|->|->| | | Prepare(1)
| |<------------X--X--X | | Promise(1,{null, null, null})
| | | | | | |
| | | | | | | !! Leader fails during broadcast !!
| X------------>| | | | | Accept!(1,Va)
| ! | | | | |
| | | | | | | !! NEW LEADER !!
| X--------->|->|->| | | Prepare(2)
| |<---------X--X--X | | Promise(2,{null, null, null})
| X--------->|->|->| | | Accept!(2,V)
| |<---------X--X--X------>|->| Accepted(2,V)
|<---------------------------------X--X Response
| | | | | | |
In the event of a proposer failure, the system must select a new proposer, usually by voting after a timeout has elapsed waiting for the old proposer to return. In the event that after choosing a new proposer, the old one comes back to life, a conflict may arise between the leaders, which can lead to a loop of the system:
Client Leader Acceptor Learner
| | | | | | |
X----->| | | | | | Request
| X------------>|->|->| | | Prepare(1)
| |<------------X--X--X | | Promise(1,{null,null,null})
| ! | | | | | !! LEADER FAILS
| | | | | | | !! NEW LEADER (knows last number was 1)
| X--------->|->|->| | | Prepare(2)
| |<---------X--X--X | | Promise(2,{null,null,null})
| | | | | | | | !! OLD LEADER recovers
| | | | | | | | !! OLD LEADER tries 2, denied
| X------------>|->|->| | | Prepare(2)
| |<------------X--X--X | | Nack(2)
| | | | | | | | !! OLD LEADER tries 3
| X------------>|->|->| | | Prepare(3)
| |<------------X--X--X | | Promise(3,{null,null,null})
| | | | | | | | !! NEW LEADER proposes, denied
| | X--------->|->|->| | | Accept!(2,Va)
| | |<---------X--X--X | | Nack(3)
| | | | | | | | !! NEW LEADER tries 4
| | X--------->|->|->| | | Prepare(4)
| | |<---------X--X--X | | Promise(4,{null,null,null})
| | | | | | | | !! OLD LEADER proposes, denied
| X------------>|->|->| | | Accept!(3,Vb)
| |<------------X--X--X | | Nack(4)
| | | | | | | | ... and so on ...
As an example of implementation, I will give a slightly modified python code of one of the github repositories :
class Proposer (object):
# 1a. Генерируется уникальное значение proposal_id (в описании алгоритма фигурирует как "N")
# и отправляется "предложение" всем acceptor
def prepare(self):
self.promises_rcvd = 0
self.proposal_id = self.next_proposal_number
self.next_proposal_number += 1
self.messenger.send_prepare(self.proposal_id)
# 2a. Получаем "обещание". Если предложение было не наше - ингорируем. Если с "обещанием"
# вернулось также принятое acceptor значение - принимаем его как значение нашего предложения.
# Если количество принятых "обещаний" равно кворуму, отправляем сообщение "принять"
def recv_promise(self, proposal_id, prev_accepted_id, prev_accepted_value):
if proposal_id != self.proposal_id:
return
if prev_accepted_id > self.last_accepted_id:
self.last_accepted_id = prev_accepted_id
if prev_accepted_value is not None:
self.proposed_value = prev_accepted_value
self.promises_rcvd += 1
if self.promises_rcvd == self.quorum_size:
if self.proposed_value is not None:
self.messenger.send_accept(self.proposal_id, self.proposed_value)
class Acceptor (object):
# 1b. Acceptor получает "предложение" от proposer. В случае, если предложение с таким номером уже приходило,
# отправляем тот же самый ответ. Если ранее приходило только предложения с меньшим номером, отправляем
# номер последнего принятого предложения и принятое значение (если таковое есть) как "обещание"
def recv_prepare(self, proposal_id):
if proposal_id == self.promised_id:
self.messenger.send_promise(proposal_id, self.accepted_id, self.accepted_value)
elif proposal_id > self.promised_id:
self.promised_id = proposal_id
self.messenger.send_promise(proposal_id, self.accepted_id, self.accepted_value)
# 2b. Получаем сообщение "принять". Если мы не обещали не принимать значения с таким номером, то
# запоминаем идентификатор и значение этого сообщения и отвечаем "принято"
def recv_accept_request(self, from_uid, proposal_id, value):
if proposal_id >= self.promised_id:
self.promised_id = proposal_id
self.accepted_id = proposal_id
self.accepted_value = value
self.messenger.send_accepted(proposal_id, self.accepted_value)
class Learner (object):
# 3. Learner получает сообщение "принято", запоминает это значение и возвращает управление клиенту
def recv_accepted(self, from_uid, proposal_id, accepted_value):
self.final_value = accepted_value
self.messenger.on_resolution( proposal_id, accepted_value )
Literature:
