Sample pen on a supercomputer Lomonosov

In this post I want to talk about my experience of calculations on the Lomonosov supercomputer. I will talk about solving the problem, frankly, for which you do not need to use SC, but academic interest is above all. Detailed information on the configuration of Lomonosov can be found here .

Data rate between nodes / processes

At first, I decided to conduct a simple test of the cluster bandwidth, and compare how much the data transfer rates differ from one thread to another a) if both threads are running on the same cluster node; b) on different. The following values ​​were evaluated using the mpitests-osu_bw test.
Peak speed at different nodes:
3.02 GB / s.
On a single host:
10.3 GB / s

A bit about the task

It is necessary to solve the diffusion equation in a rather simple region. We have a linear equation in par. We will solve it without flow, i.e. at the boundaries 1, 2, 4, the derivative is normal to the wall 0, and at the boundary 3, the concentration is determined by the given function g (t). Thus we get a mixed boundary value problem. We will solve it by the finite difference method (very inefficient, but simple).

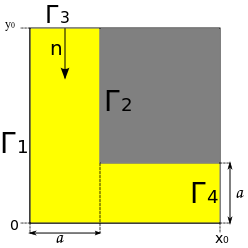
About Parallelization

To solve this problem, I used openMPI / intelMPI (a separate post should be devoted to comparing compilers in practice). I will not delve into the numerical scheme, for there is Wikipedia and I will only say that I used an explicit scheme. I used the block distribution of the area so that each stream is given several areas and if the data that is transmitted from the previous area is zero, then the area is not considered. The extreme columns / rows of the blocks are designed to receive data from neighboring streams.

Grid parameters used in calculations

Number of nodes in the grid: 3 * 10 ^ 6
Step on the grid: 0.0007.
Physical diffusion time: 1 s
Time step: 6.5 * 10 ^ -7
D: 0.8
Initial concentration at the border of 3 0.01 mol.

A little about the law of Amdal

Jim Amdahl formulated a law illustrating the limitation of the performance of a computer system with an increase in the number of computers. Suppose that it is necessary to solve some computational problem. Let α be the fraction of the algorithm that is executed sequentially. Then, respectively, 1-α is executed in parallel and can be parallelized on p-nodes, then the acceleration obtained on a computing system can be obtained as

Let's pass to the most interesting to the results and results of parallelization

Run times on various number of threads

number of percent.	1	2	8	16	32	64	128
time min	840	480	216	112	61	46	41

We approximate the calculation times by Amdahl's law.

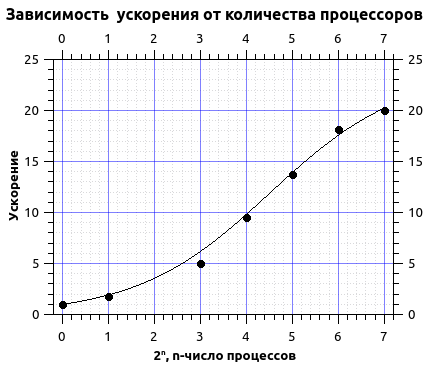
From the approximation, I got the share of the sequential code of the order of 4.2% and the maximum acceleration of the order of 20 times. As you can see from the graph, the curve goes to a plateau, from this we can conclude that the maximum acceleration is achieved and further entrainment of the number of processors is impractical. Moreover, in this case, with an increase in the number of processes over 200, I received a decrease in acceleration, this is due to the fact that with an increase in the number of processes, their irrational use begins, i.e. the number of rows in the grid becomes commensurate with the number of processes and more time is spent on exchanges and this time makes a significant contribution during the calculation.

Some notes

The SC uses the sbatch task management system and there are several queues test, regular4, regular6, gputest, gpu. For this task, I used the regular4 queue, the waiting time in which can reach three days (in practice, the waiting time is 17-20 hours).