"The matrix of friendship." The oldest social graph for the smallest

It happened on the first of September, the next academic year, flowers, sweets, tears of happiness and this is all, and in preparation for the lecture at the institute I came across very interesting data . I looked to have such a thing possible to quickly and beautifully draw in GePhi , and came across the story of Johannes Delitzch (Johannes Delitsch). Delić worked in Leipzig as a primary school teacher and in the 1880 school year he collected information about who is friends with whom in his class. And this, along the way, is one of the first documented social graphs.

The classes at that time were large (in this particular case there were as many as 53 students), and the old Johannes, as I understood it, until 1880 was working only as a tutor. So at the beginning of the new school year, when I saw my vast fourth “A” (I honestly don’t know what the letter was there, it’s not so important), Johannes felt a little sad. As a man, he, apparently, was active and decided to better understand the social relations of the mob entrusted to him.

Data

Johannes was not a modern sociologist. He was a schoolteacher, so his data collection methodology was pretty, ahem, eclectic. He talked with the students, and read their homework, and "watched them communicate in a group." The result was a rather spreading set of data on the basis of which Delitzsch wrote an article in Zeitschrift für.

Kinderforschung (any words in German sound and are written very scary, sorry in advance, but the literal translation of the "Journal for the Study of Children" sounds in Russian even more creepy). Johannes, as I understood, was primarily interested in how the child's academic performance and his popularity among classmates are related, therefore, in addition to a directed graph describing who is friends with whom, Delitzch also gives a student rating (from the most successful to the most unsuccessful) and some interesting parameters. For example, there were four replicators in the class, they are highlighted in dataset. Back in the class was a guy named Lasch (Lasch), whose grandmother was a pastry chef. Delitch noted that Lash treats other children with sweets and noted this in his data. He also separately identified children who had health problems, such as anemia,

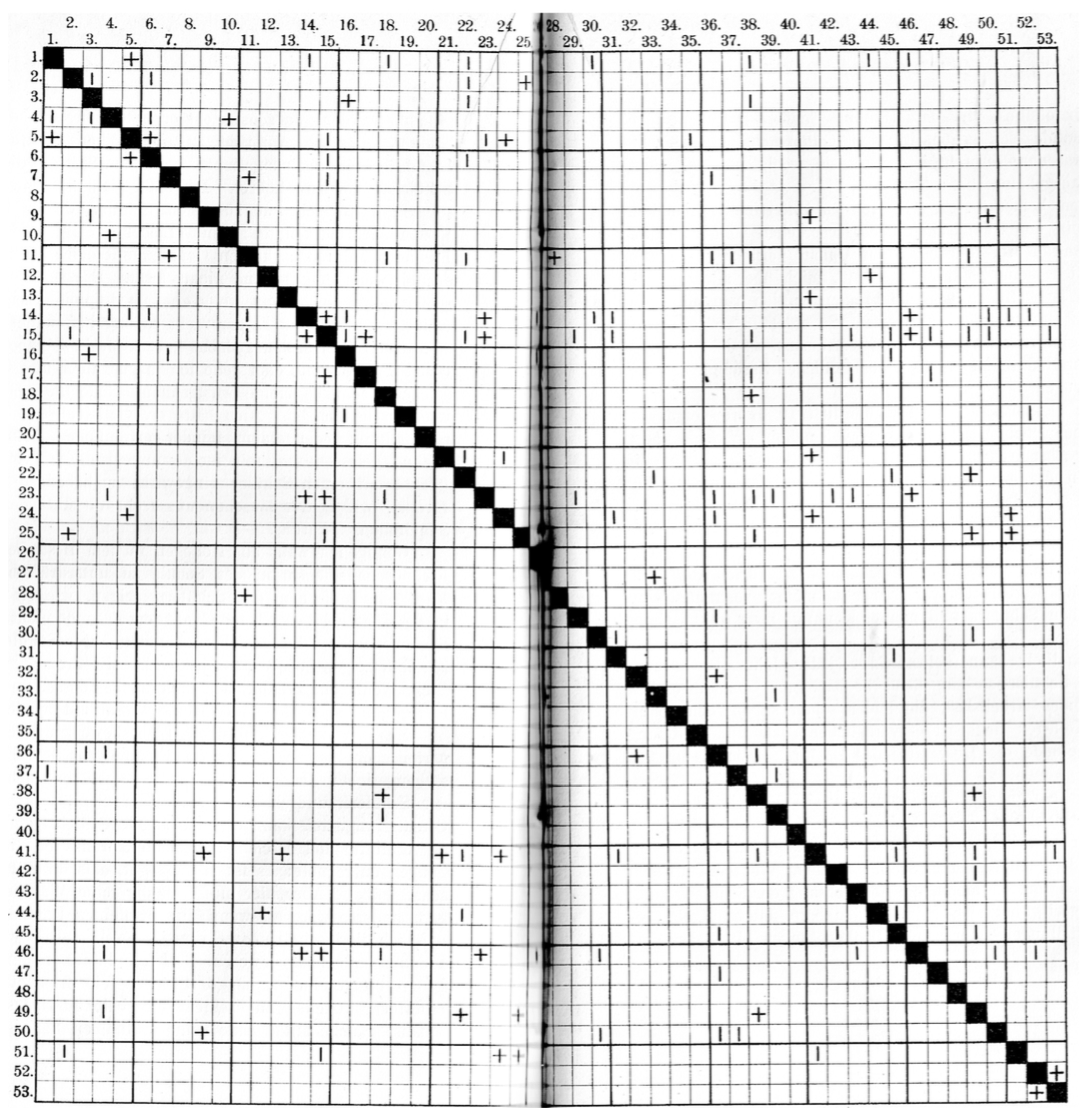
"The matrix of friendship" describes who and who is friends. The graph is directed, because Hans can consider Friedrich a friend, and Friedrich, maybe, he wanted to sneeze on Hans.

The best people of our class

Let's poke this social graph in GePhi, calculate, for example, PageRank and color the vertices.

More "influential" students painted in a more saturated color.

Let's “highlight” seven students with the highest PageRank (I will explain later why it is seven, for now let's just consider seven as a fundamental constant). That's what happens if you select the seven vertices of the graph, which have the highest PageRank.

The opinion leaders of the fourth "A" in 1880.

We already spoke about these guys! Firstly, all four replica "in the top." I decided to single out seven people, because one of the four repetition years by the name of Schnabel is not very cool. It has the seventh PageRank value. At the same time, Pfeil (Pheil) and Fetter (Vetter) followers confidently (and with a large margin) occupy the first and second line on the “authority” list, and Schubert, the second yearbook, take the fourth, second only “Lasha” in “authority” (there is little that can compete with the distribution of candy). Schnabel is only seventh. Above him in terms of credibility, the best student in the class of Schlegel (Schlegel) and the fifth in terms of academic achievement student Meinhold (Meinhold). We don’t know anything about this Meinhold, we didn’t leave any special information about him, so we’ll denote him in the picture as a "strange guy."

Tambourines and modularity class calculation

In GePhi there is a tool to find in our fourth "A" group "by interest". The algorithm is described here , and the implementation used by GePhi is here . The general idea is that the algorithm tries to assess which communities within the network are more dense. For several passes, the algorithm can give a different breakdown into communities, so everything that comes next is just a rite and beats to a tambourine on the basis of a single result, which does not make the process less fun. So, in these colors, our fourth "A" colorized search engine communities.

Tell me who you are friends with, and I will say that you are in vain.

Let's see what happened. All of our seven most influential guys fell into four main communities. Three "cool" repeaters Pfayl, Vetter and Schubert got into the community, painted on the picture in green. "Nekrutoy" repeater year-old Schnabel and the best student of the class Schlegel were in a community painted in purple. Finally, the candy distributor Lash got into the community indicated in the picture by light blue. Meinhold remains a mystery man. He got into a small group of "chosen ones", in which there are only three students (including himself), she is painted in dark gray. Of the four children who had health problems, two are not friends with anyone at all, and the other two are in a blue community.

Well. Much is starting to clear. Schnabel, apparently, is not such a "cool" replicator, because instead of hanging out with cool guys, he communicates with some nerds with whom friend-boy Schlegel is friends (it is interesting that Schnabel and Schlegel themselves are not friends, but stably fall into one community when calculating network modularity). Lash and his candy formed a community of guys who are not taken into either the nerds or the bad guys, but Meinhold ... Hmmm ... Who is Meinhold? Let's see who else with him "in the crowd." Two more students who have fallen into the same community with him are Meier (Meier, fourth in the ranking of students) and Flush (Flasch, thirty-fifth in the rating of students). Hmmm ... Three dudes who no longer communicate well with anyone, but two of which are learning well ...

Shot from Superbad movie.

In short, I like to think of these three guys as a trinity of geeks from 19th century Germany. Two study well, and the third one doesn’t communicate with anyone, just after the lessons of a giant humanoid robot, or krigsmarine, or something worse. Not the point.

Let's translate the ranking of German students in the average grade. We will generate something similar to the normal distribution on the interval from 2 to 5 (the Germans have an inverse scale of assessments, but we will do everything for our understanding on our usual scale, when 2 - did not pass, and 5 - handsome). Let us compare each student with his average score so that when ranking by this average score would be obtained the same rating as in the Delich data. Now let's see what is the average grade of the students in each of these four groups. And at the same time, how many people on average a friend of each group is friends with, and how many people are on average friendly with him. It turns out this:

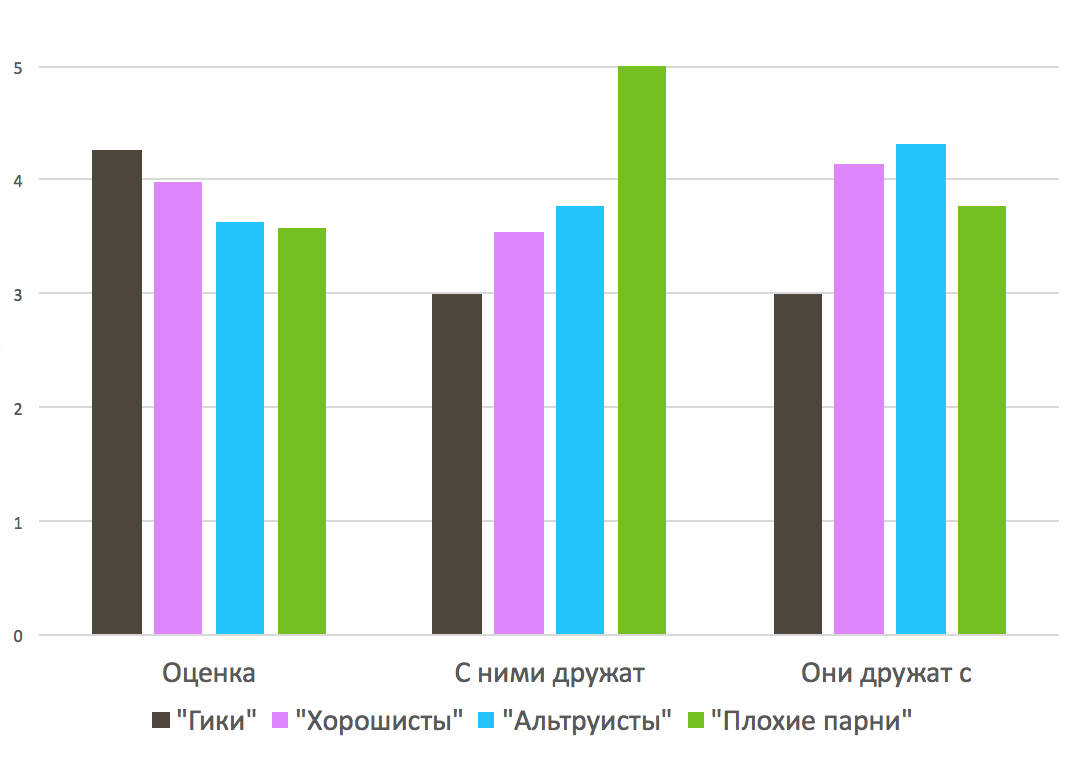
The average score and the average in- and out-degree for four groups. The colors match the coloring of the graph.

Geeks, in general, learn well, but they don’t want to be friends, and no one is going to be friends with them. Horoshisty from the party Schlegel and Schnabel learn on average worse geeks, but in social terms, they have all the better. Altruists (as I called the group into which Lash distributed the candy) entered are lousy, but they are friends with other children most actively (if not mutually). Finally, the bad guys learn the worst of them all, but they are very popular (they want to be friends with them), although in terms of the number of people with whom they are friends, they are not far from geeks.

Let's draw with whom the representatives of different communities are friends.

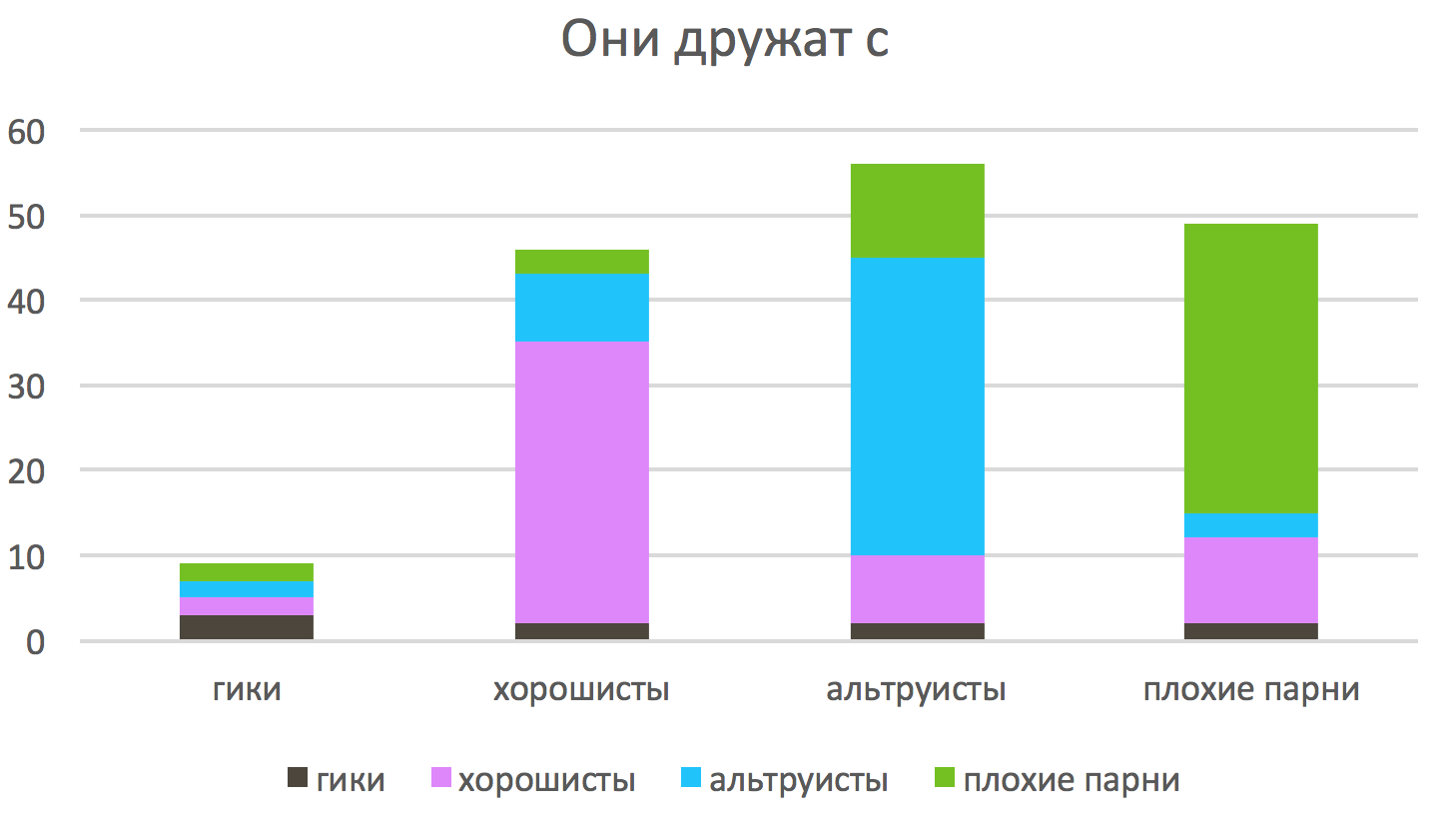
Each community is most friendly within itself, but interacts with other communities differently.

See how fun it is! Altruists consider their friends a lot of horoshist and a lot of bad guys. Bad guys altruists do not particularly favor, but here are some horoshisty consider their friends. Well-judged, judging by everything, they are not thrilled by the friendship with the bad guys, but altruists with their smiling faces and freebies candy cause their reserved interest.

If for some reason it is more interesting for you to look from the other side, then here is another bonus picture.

Each community is most friendly within itself, but interacts with other communities differently.

Here is such a fun data set in the first week of autumn. In 2014, this article re-opened the data on our fourth “A” to the world . The fact is that after the first world Germany there was no time for pedagogy, so the data collected by Delic was forgotten for a long time, and now it turns out that this is almost the first detailed documented social graph. So it goes.

The original data was published in an article:
Delitsch, J., 1900. Über Schülerfreundschaften in einer Volksschule. Zeitschrift für Kinderforschung 5, 150–162.

PS I was here several times asked what this is all morality. I think the moral is here.

First, even a few columns of numbers can hide the drama. Yes, even what.

Secondly, for any person working with data, the answer to the question "what is the moral here?" comes down to the question "what is the quality metric here?"

If the metric is performance, then it is better to be friends with excellent students. All repetitioners, in fact, in the ranking of the class is not in the top, but not at the bottom in terms of performance. They hang out somewhere in the middle, but other children in their community learn much worse. Perhaps the comparatively good performance of the repetition years is connected with the fact that the German school of the nineteenth century paid quite a lot of attention to physical training and sports, so that part of the repetition of performance repetition was too high due to the fact that they are simply physically stronger. The community around Schlegel and the community of geeks, in spite of this bias, learn much better than the community that has formed around the repetitioners.

If a metric is popular among peers, then throwing candies around is quite an expensive and not very effective way of recruiting this very popularity. On the one hand, it works: Lash is the third most popular student in the class. On the other hand, the "quality" of his community (in terms of social popularity) is rather low. That is, candy allows you to become popular among not very popular people. Other popular guys are not on friendly terms with Lash (neither the replayers nor the best student of the Schlegel class).

Finally, if a metric is the number of “real” friends (where a true friend is not a person you are friends with, but only those of your friends who are friends with you), then it’s the same as being a repetition year-old.