Home network current measurement
There is a whole class of devices called Ethernet Relay that allow you to remotely control connected loads over the network. Most of them are quite expensive - closer to $ 100, and are obviously inferior in price and flexibility to a bunch of, say, Raspberry Pi + PiFace . But what if the task is not only to turn on / off the load, but also to measure the flowing current? This requires the actual sensor (on a shunt or Hall effect) and an ADC (the Raspberry Pi does not contain a built-in ADC). As a sensor, you can take an inexpensive ACS712, and as an ADC, for example, ADC-Pi .
I did not like the ADC-Pi for two reasons:
All Arduino already have an ADC (8-bit, but this is enough), sketches for Arduino are performed with the necessary stability, there are various options for communicating with the Raspberry Pi, the easiest of which is a USB cable. And of course, an attractive price.
The bundle I used is shown in the picture.

Measuring the current strength is a simple task, if not for one “but”: the physical sensors are “noisy”. The figure shows an example of the actual and calculated current indicators for my circuit with 512 consecutive measurements.

Thus, the task of measuring the alternating current is to calculate the amplitude of the sine wave from a set of actual measurements containing a significant proportion of errors.
AC formula (who forgot - see wiki )
i = Im sin (ωt + ψ)
where:
Im is the maximum current value
ω is the angular frequency
t is the time (serial number) of the change
ψ is the initial phase of the current
You can try to find the necessary parameters, using analytical tools. And here we are waiting for a pleasant surprise: last fall (2013), Wolfram released a version of its wonderful Mathematica package for the Raspberry Pi . Free (for home use). And we can use it to analyze the data read from the sensor.
An example of invoking a calculation package in Raspberry Pi:
The calc_current.wl script itself below with comments:
Read data from a file passed as a parameter. The file contains lines of the form <dimension number>, <value>.
When the data is read, a Fast Fourier Transform can be done to determine approximately the number of sinusoidal cycles in an existing sample. The time dependence of the current strength is nonlinear, and the approximate angular velocity calculated by the FFT and transmitted as the initial value will sharply increase the chances of choosing the right sinusoid parameters.
If the maximum FFT value does not differ significantly from the average for the sample, we can conclude that there is no pronounced sinusoid, all indicators are “noise”, and the actual current is zero.
If a pronounced sinusoid is found, you can try to choose the parameters of the function using the most pronounced cycle to calculate the initial value of the angular velocity.
Knowing the physical characteristics of the ADC (dimension 1024, the base voltage 5V) and the sensor (in my version 0.185V / A), we can calculate the effective current strength:
The proposed method works in most cases. The number of measurements when NonlinearModelFit could not correctly select the parameters of the sine wave was about 5 percent. However, each measurement takes a lot of time - I have an average of 5 seconds - to run the wolfram application. Therefore…
Since the frequency of the alternating current in the network is stable and is (in Russia) 50 Hz, the angular velocity can be calculated in advance and instead of non-linear regression, get a linear regression. In fact,
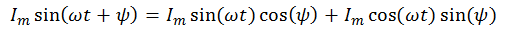
or

Differentiating with respect to X and Y, we obtain a system of linear equations:

Solving the system according to Kramer, we obtain the coefficient values:

Then, according to the Pythagorean theorem, the maximum current value will be: An

Arduino sketch that implements this algorithm can be found on Github . The method provides good measurement accuracy: for the circuit in the figure, the measured current value was stable 0.13A, which corresponds to a consumption of 29.9 W at a voltage of 230V. The rating of the light bulb that served as the load is 30 watts.
By the way, for Arduino there are also shields with relays and all the control and monitoring functions of the load can be implemented on this platform. In this case, the Raspberry Pi will be used only for organizing a convenient user interface, for example, through a web server and as a sheduler.
I did not like the ADC-Pi for two reasons:
- at the frequency of measurements that is required to determine the strength of the alternating current in the network, this ADC gives a very large error (most likely I did not fully understand the registers)
- using this ADC in conjunction with the Raspberry Pi under Linux it is difficult to provide the necessary stability of the measurement period. Installing and configuring RTOS Linux only for this task seemed to me too complex, especially since there is a simpler and more proven solution: Arduino
All Arduino already have an ADC (8-bit, but this is enough), sketches for Arduino are performed with the necessary stability, there are various options for communicating with the Raspberry Pi, the easiest of which is a USB cable. And of course, an attractive price.
The bundle I used is shown in the picture.

Measuring the current strength is a simple task, if not for one “but”: the physical sensors are “noisy”. The figure shows an example of the actual and calculated current indicators for my circuit with 512 consecutive measurements.

Thus, the task of measuring the alternating current is to calculate the amplitude of the sine wave from a set of actual measurements containing a significant proportion of errors.
Attempt number one
AC formula (who forgot - see wiki )
i = Im sin (ωt + ψ)
where:
Im is the maximum current value
ω is the angular frequency
t is the time (serial number) of the change
ψ is the initial phase of the current
You can try to find the necessary parameters, using analytical tools. And here we are waiting for a pleasant surprise: last fall (2013), Wolfram released a version of its wonderful Mathematica package for the Raspberry Pi . Free (for home use). And we can use it to analyze the data read from the sensor.
An example of invoking a calculation package in Raspberry Pi:
pi@raspi ~ $ wolfram -script calc_current.wl datafile=/tmp/data.csvThe calc_current.wl script itself below with comments:
Read data from a file passed as a parameter. The file contains lines of the form <dimension number>, <value>.
data=Import[$CommandLine[[4]]]When the data is read, a Fast Fourier Transform can be done to determine approximately the number of sinusoidal cycles in an existing sample. The time dependence of the current strength is nonlinear, and the approximate angular velocity calculated by the FFT and transmitted as the initial value will sharply increase the chances of choosing the right sinusoid parameters.
fourier=Take[Abs[Fourier[data[[All,2]]]],{2,256}]If the maximum FFT value does not differ significantly from the average for the sample, we can conclude that there is no pronounced sinusoid, all indicators are “noise”, and the actual current is zero.
topcycle=Ordering[fourier,-1]avg=Mean[fourier]top=fourier[[topcycle[[1]]]]If[top < 10 * avg, Print["No AC"]; Exit[]]If a pronounced sinusoid is found, you can try to choose the parameters of the function using the most pronounced cycle to calculate the initial value of the angular velocity.
nlm=NonlinearModelFit[data, a Sin[b x + c]+d, {a,{b, 2 Pi * topcycle[[1]] / 512}, c, d},x]Knowing the physical characteristics of the ADC (dimension 1024, the base voltage 5V) and the sensor (in my version 0.185V / A), we can calculate the effective current strength:
imax=Abs[nlm["BestFitParameters"][[1]][[2]]] / (1024 / 5 * 0.185)Print["Imax=", imax]iefc=imax / Sqrt[2]Print["Iefc=", iefc]Print["Power=", iefc * 230]The proposed method works in most cases. The number of measurements when NonlinearModelFit could not correctly select the parameters of the sine wave was about 5 percent. However, each measurement takes a lot of time - I have an average of 5 seconds - to run the wolfram application. Therefore…
Attempt number two
Since the frequency of the alternating current in the network is stable and is (in Russia) 50 Hz, the angular velocity can be calculated in advance and instead of non-linear regression, get a linear regression. In fact,
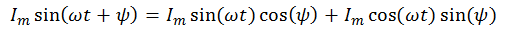
or

Differentiating with respect to X and Y, we obtain a system of linear equations:

Solving the system according to Kramer, we obtain the coefficient values:

Then, according to the Pythagorean theorem, the maximum current value will be: An

Arduino sketch that implements this algorithm can be found on Github . The method provides good measurement accuracy: for the circuit in the figure, the measured current value was stable 0.13A, which corresponds to a consumption of 29.9 W at a voltage of 230V. The rating of the light bulb that served as the load is 30 watts.
By the way, for Arduino there are also shields with relays and all the control and monitoring functions of the load can be implemented on this platform. In this case, the Raspberry Pi will be used only for organizing a convenient user interface, for example, through a web server and as a sheduler.
