December 17, 2013 at 08:36An example of solving the multiple regression problem using Python
Introduction
Good afternoon, dear readers.
In past articles, on practical examples, I have shown how to solve classification problems ( credit scoring problem ) and the basics of textual information analysis ( passport problem ). Today I would like to touch upon another class of problems, namely , regression restoration . Tasks of this class are usually used in forecasting .
As an example of solving the forecasting problem, I took the Energy efficiency dataset from the largest UCI repository . As a tradition, we will use Python with the pandas and scikit-learn analytic packages .
Description of the data set and problem statement
A dataset is given that describes the following room attributes:
| Field | Description | A type |
|---|---|---|
| X1 | Relative compactness | Float |
| X2 | Area | Float |
| X3 | Wall area | Float |
| X4 | Ceiling area | Float |
| X5 | Total height | Float |
| X6 | Orientation | INT |
| X7 | Glazing area | Float |
| X8 | Distributed glazing area | INT |
| y1 | Heating load | Float |
| y2 | Cooling load | Float |
In it
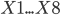are the characteristics of the premises on the basis of which the analysis will be carried out, and 
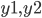- the load values that need to be predicted.Preliminary data analysis
First, upload our data and look at them:
from pandas import read_csv, DataFrame
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.cross_validation import train_test_split
dataset = read_csv('EnergyEfficiency/ENB2012_data.csv',';')
dataset.head()
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | Y1 | Y2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 2 | 0 | 0 | 15.55 | 21.33 |
| 1 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 3 | 0 | 0 | 15.55 | 21.33 |
| 2 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 4 | 0 | 0 | 15.55 | 21.33 |
| 3 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 5 | 0 | 0 | 15.55 | 21.33 |
| 4 | 0.90 | 563.5 | 318.5 | 122.50 | 7 | 2 | 0 | 0 | 20.84 | 28.28 |
Now let's see if any attributes are related. This can be done by calculating the correlation coefficients for all columns. How to do this was described in a previous article :
dataset.corr()
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | Y1 | Y2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 1.000000e + 00 | -9.919015e-01 | -2.037817e-01 | -8.688234e-01 | 8.277473e-01 | 0.000000 | 1.283986e-17 | 1.764620e-17 | 0.622272 | 0.634339 |
| X2 | -9.919015e-01 | 1.000000e + 00 | 1.955016e-01 | 8.807195e-01 | -8.581477e-01 | 0.000000 | 1.318356e-16 | -3.558613e-16 | -0.658120 | -0.672999 |
| X3 | -2.037817e-01 | 1.955016e-01 | 1.000000e + 00 | -2.923165e-01 | 2.809757e-01 | 0.000000 | -7.969726e-19 | 0.000000e + 00 | 0.455671 | 0.427117 |
| X4 | -8.688234e-01 | 8.807195e-01 | -2.923165e-01 | 1.000000e + 00 | -9.725122e-01 | 0.000000 | -1.381805e-16 | -1.079129e-16 | -0.861828 | -0.862547 |
| X5 | 8.277473e-01 | -8.581477e-01 | 2.809757e-01 | -9.725122e-01 | 1.000000e + 00 | 0.000000 | 1.861418e-18 | 0.000000e + 00 | 0.889431 | 0.895785 |
| X6 | 0.000000e + 00 | 0.000000e + 00 | 0.000000e + 00 | 0.000000e + 00 | 0.000000e + 00 | 1.000000 | 0.000000e + 00 | 0.000000e + 00 | -0.002587 | 0.014290 |
| X7 | 1.283986e-17 | 1.318356e-16 | -7.969726e-19 | -1.381805e-16 | 1.861418e-18 | 0.000000 | 1.000000e + 00 | 2.129642e-01 | 0.269841 | 0.207505 |
| X8 | 1.764620e-17 | -3.558613e-16 | 0.000000e + 00 | -1.079129e-16 | 0.000000e + 00 | 0.000000 | 2.129642e-01 | 1.000000e + 00 | 0.087368 | 0.050525 |
| Y1 | 6.222722e-01 | -6.581202e-01 | 4.556712e-01 | -8.618283e-01 | 8.894307e-01 | -0.002587 | 2.698410e-01 | 8.736759e-02 | 1.000000 | 0.975862 |
| Y2 | 6.343391e-01 | -6.729989e-01 | 4.271170e-01 | -8.625466e-01 | 8.957852e-01 | 0.014290 | 2.075050e-01 | 5.052512e-02 | 0.975862 | 1.000000 |
As you can see from our matrix, the following columns correlate with each other (The value of the correlation coefficient is more than 95%):
- y1 -> y2
- x1 -> x2
- x4 -> x5
Now let's choose which columns of our pairs we can remove from our sample. To do this, in each pair, we select the columns that have a greater effect on the predicted values of Y1 and Y2 and leave them, and delete the rest.
As you can see, matrices with correlation coefficients on y1 , y2 have X2 and X5 more than X1 and X4, so we can delete the last columns.
dataset = dataset.drop(['X1','X4'], axis=1)
dataset.head()
In addition, it can be noted that the fields Y1 and Y2 are very closely correlated with each other. But, since we need to predict both values, we leave them “as is”.
Model selection
Separate the forecast values from our sample:
trg = dataset[['Y1','Y2']]
trn = dataset.drop(['Y1','Y2'], axis=1)
After processing the data, you can proceed to the construction of the model. To build the model we will use the following methods:
The theory of these methods can be read in the course of lectures by K.V. Vorontsov on machine learning .
We will estimate using the coefficient of determination ( R-squared ). This coefficient is determined as follows:
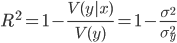
where
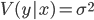is the conditional variance of the dependent quantity y by the factor x . The coefficient takes on a value in the gap
and the closer it is to 1, the stronger the dependence. Well, now you can go directly to building a model and choosing a model. Let's put all our models in one list for the convenience of further analysis:
models = [LinearRegression(), # метод наименьших квадратов
RandomForestRegressor(n_estimators=100, max_features ='sqrt'), # случайный лес
KNeighborsRegressor(n_neighbors=6), # метод ближайших соседей
SVR(kernel='linear'), # метод опорных векторов с линейным ядром
LogisticRegression() # логистическая регрессия
]
So the models are ready, now we will break our initial data into 2 subsamples: test and training . Those who read my previous articles know that this can be done using the train_test_split () function from the scikit-learn package:
Xtrn, Xtest, Ytrn, Ytest = train_test_split(trn, trg, test_size=0.4)
Now, since we need to predict 2 parameters
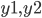, we need to build a regression for each of them. In addition, for further analysis, you can write the results to a temporary DataFrame . You can do it this way: #создаем временные структуры
TestModels = DataFrame()
tmp = {}
#для каждой модели из списка
for model in models:
#получаем имя модели
m = str(model)
tmp['Model'] = m[:m.index('(')]
#для каждого столбцам результирующего набора
for i in xrange(Ytrn.shape[1]):
#обучаем модель
model.fit(Xtrn, Ytrn[:,i])
#вычисляем коэффициент детерминации
tmp['R2_Y%s'%str(i+1)] = r2_score(Ytest[:,0], model.predict(Xtest))
#записываем данные и итоговый DataFrame
TestModels = TestModels.append([tmp])
#делаем индекс по названию модели
TestModels.set_index('Model', inplace=True)
As you can see from the code above,
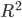the r2_score () function is used to calculate the coefficient . So, the data for analysis are obtained. Now let's build the graphs and see which model showed the best result:
fig, axes = plt.subplots(ncols=2, figsize=(10,4))
TestModels.R2_Y1.plot(ax=axes[0], kind='bar', title='R2_Y1')
TestModels.R2_Y2.plot(ax=axes[1], kind='bar', color='green', title='R2_Y2')
Analysis of the results and conclusions
From the graphs above, we can conclude that the RandomForest method (the random forest) handled the task better than others . Its determination coefficients are higher than the others in both variables: For
further analysis, let's re-train our model:
model = models[1]
model.fit(Xtrn, Ytrn)
A close examination may raise the question of why the previous time we divided the dependent sample Ytrn into variables (in columns), but now we do not.
The fact is that some methods, such as RandomForestRegressor , can work with several predicted variables, while others (for example, SVR ) can work with only one variable. Therefore, at the previous training, we used column breaks to avoid errors in the process of constructing some models.
It is, of course, good to choose a model, but it would be nice to have information on how each factor will affect the predicted value. For this, the model has the feature_importances_ property .
Using it, you can see the weight of each factor in the final models:
model.feature_importances_
array ([0.40717901, 0.11394948, 0.34984766, 0.00751686, 0.09158358,
0.02992342])
In our case it can be seen that the overall height and area affect the load most of all during heating and cooling. Their total contribution to the forecast model is about 72%.
It should also be noted that according to the above scheme, you can see the influence of each factor separately on heating and separately on cooling, but since these factors correlate very closely with each other (
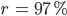), we made a general conclusion on them both which was written above .Conclusion
In the article, I tried to show the main stages in the regression analysis of data using Python and the analytical packages pandas and scikit-learn .
It should be noted that the data set was specially chosen so as to be as formalized as possible and the initial processing of the input data would be minimal. In my opinion, the article will be useful to those who are just starting their way in data analysis, as well as those who have a good theoretical base, but who choose tools for work.