Elliptical cryptography: theory

Hi% username%!
Recently, a very controversial article was published on the habra , entitled "Experts urge to prepare for a crypto apocalypse . " Honestly, I do not agree with the authors' conclusions that there is a “golacteko danger”, all will soon crack and buckwheat will rise in price. However, this is not what I want to talk about.
In the comments on that article, I expressed the opinion that in some respects the speakers are right and it is high time to switch to elliptical cryptography. Well, in fact, did anyone see the ECDSA certificate on the Internet? Although the standard is already almost 13 years old, we continue to use the good old RSA as usual. In general, I said this, and as often happens, I thought about whether the transition to the “elliptic” is so necessary? And what kind of beast is this elliptical cryptography? What are the pros, cons, subtleties. In a word, let's understand.

Elliptical curves

An elliptic curve is a set of points described by the Weierstrass equation:

You can see typical variations of elliptic curve graphs under the spoiler:

The elliptic curves shown in the first 4 figures are called smooth. While the two lower curves belong to the so-called singular elliptic curves.
For smooth elliptic curves, the following inequality holds:

Whereas for singular curves this condition, surprise, is not satisfied.
If you are going to independently develop a cryptographic product that supports the “elliptic” it is very important to remember the following fact:
You cannot use singular curves in EDS schemes. We will touch on this topic in detail, but now we’ll just say that using singular curves you risk significantly reducing the resistance of the EDS scheme.
Arithmetic operations in elliptic cryptography are performed on the points of the curve. The main operation is "addition".
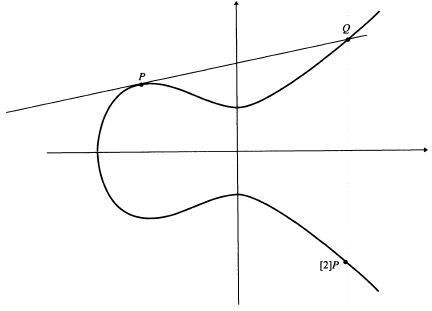
The addition of two points is easily represented graphically:

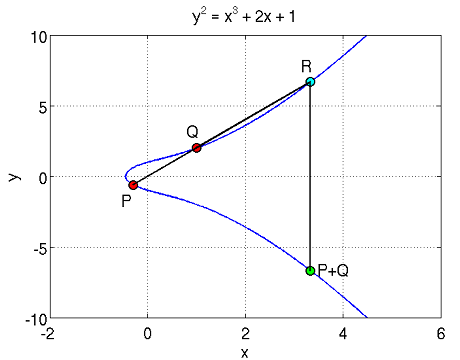
as can be seen from the figure, to add the points P and Q, it is necessary to draw a straight line between them, which will necessarily intersect the curve at some third point R. We reflect the point R relative to the horizontal coordinate axis and get the desired point P + Q.

Algebraic representation of "addition"

We write the addition of two points in the form of a formula:

Let the coordinates of the point P be (x _p , y _p ), and the coordinates of the point Q, respectively (x _q , y _q ). We calculate

and then the coordinates of the point P + Q will be equal to:

Elliptic Curves in Cryptography

It remains to clarify only one detail. All the curves discussed above are elliptic curves over real numbers. And this leads us to the problem of rounding. That is, using curves over real numbers, we can’t get a bijection between the source text and the encrypted data. In order not to bother with rounding in cryptography, only curves above the final fields are used. This means that an elliptic curve is a set of points whose coordinates belong to a finite field.

In cryptography, two types of elliptic curves are considered: above a finite field , a residue ring modulo a prime number. And above the field is a binary finite field.
Elliptic curves over a field have one important advantage, field elementscan be easily represented as n-bit code words, this allows you to increase the speed of hardware implementation of elliptic algorithms.

All mathematical operations on elliptic curves over a finite field are performed according to the laws of a finite field over which an elliptic curve is constructed. Those. to calculate, for example, the sum of two points of the curve E over the residue ring, all operations are performed modulo p.

However, there are pitfalls. If we add two identical elements from a binary finite field, we will get 0 as a result, because addition occurs modulo 2. This means that the characteristic of such a field is 2. But an elliptic curve of the form

the characteristics described above over the field of characteristics 2 or 3 become singular, and as already noted above, this is an unsuccessful idea to use singular curves in cryptography.

Therefore, curves of the form are used over the binary finite field:


Another important concept of elliptic cryptography is the order of the elliptic curve , which shows the number of curve points over the finite field.
Hasse's theorem states that if N - the number of points of the curve defined over a field with q elements Zq then equality:


Since the binary finite field consists of 2 ⁿ elements we can say that the order of the curve is equal to where .

The number t has the following definition:
an elliptic curve over a binary finite field is called supersingular if t is divided by the characteristic field (in the case of a binary field, the characteristic is 2) without remainder.
Of course, all this is to the fact that supersingular curves cannot be used in EDS schemes . The strict recommendation not to use singular and supersingular curves for digital signature has one very good reason, but more on that later.

Elliptic Curve Cryptography

The points of an elliptic curve over a finite field represent a group. And as we noted above, the addition operation is defined for this group.
Accordingly, we can represent the multiplication of k by G as G + G + .. + G with k terms.

Now imagine that we have a message M represented as an integer. We can encrypt it using the expression
C = M * G.
The question is how difficult it is to restore M, knowing the parameters of the curve E (a, b), the ciphertext C and the point G.
This problem is called the discrete logarithm on the elliptic curve and does not have a quick solution. Moreover, it is believed that the discrete logarithm problem on an elliptic curve is more difficult to solve than the discrete logarithm problem in finite fields.

The fastest methods developed for finite fields are useless in the case of elliptic curves.
So for solving the discrete logarithm there are quite fast algorithms having complexity , where c and d are some constants, and p is the field size. Such algorithms are called subexponential and make it relatively easy to open the discrete logarithm in the final field, if the field size is not chosen very large, of the order of 2 ¹⁰²⁴ .
At the same time, the fastest methods for solving the discrete logarithm on an elliptic curve have complexity , where q is the number of points of the elliptic curve.
Thus, to ensure a level of durability of 2 ⁸⁰ operations, it is necessary that q = 2 ¹⁶⁰. I recall that in order to get a similar level of complexity when calculating a discrete logarithm in a finite field, a field of order q = 2 ^{1024 is} needed .

However, it should be noted that since the power of computer technology is constantly increasing, the q value will constantly increase. But since the graphs of the functions and differ sharply from each other, in the group of points of the elliptic curve q will grow much more slowly than in an arbitrary finite field.

Attack options

1. Polygum-Hellman Algorithm . An algorithm for solving a discrete logarithm. Suppose that n is the number of points in an elliptic curve. Let the number n be decomposed into primes p ₁ , p ₂ , .., p _n . The essence of the method is to find discrete logarithms modulo the number p _i , and then obtain a general solution using the Chinese remainder theorem . The attack allows us to reduce the discrete logarithm problem in a large field n to the same problem, but with a much smaller field p. In order to resist the attack, you just need to choose curves whose number of points is divided by a very large prime number q≈n.
2. The Shanks algorithm , better known as baby steps / giant steps. A typical example is time memory trade off. For a group of size n, tables of size n ^{1/2 are} calculated , then this table searches for the desired item. The complexity of the algorithm .
3. Vulnerability of singular and supersingular curves . I have already mentioned that for solving the discrete logarithm problem there are no subexponential methods of solution. In fact, there is one caveat, there are such methods, but only for a certain kind of curves: singular and supersingular. The special properties of such curves make it possible to reduce the discrete logarithm problem on an elliptic curve to the discrete logarithm problem in a finite field. Accordingly, for such a class of curves, standard keys of 160-320 bits in size will be fatally vulnerable, which will allow attackers to reveal the secret key in a relatively short time.
4. Vulnerability of anomalous curves Let me remind you that the number of points of an elliptic curve is calculated by the formula
   n = q + 1-t , where q is the size of the initial field. And that a curve is called supersingular if t is divisible by 2.
   Therefore, at first glance it might seem like a good idea to use curves in which the number of points is q, i.e. t = 1.
   However, such curves are called anomalous, and solving the discrete logarithm of anomalous elliptic curves is an even simpler problem than for supersingular and singular curves.

To summarize

Based on the foregoing, we write down the main advantages and disadvantages of elliptic cryptography:
So, the main advantages:

1. A much shorter key length compared to the "classical" asymmetric cryptography.
2. The speed of elliptical algorithms is much higher than that of classical ones. This is explained both by the size of the field and the use of a binary final field structure closer to computers.
3. Due to the short key length and high speed of operation, asymmetric cryptography algorithms on elliptic curves can be used in smart cards and other devices with limited computing resources.

The main disadvantages of elliptical cryptography:

1. All the advantages of elliptic cryptography follow from one specific fact:
   for the discrete logarithm problem on elliptic curves, there are no subexponential decision algorithms. This allows you to reduce key length and increase productivity. However, if such algorithms appear, it will mean the collapse of elliptical cryptography.
2. Elliptical cryptography is very difficult. Not that I considered ordinary asymmetric cryptography a very simple thing. But the "elliptic" is a huge number of subtleties that must be taken into account. From the selection of an elliptic curve to the generation of keys. With a massive transition to elliptic, most likely there will certainly be a large number of errors and vulnerabilities that have already been worked out for more familiar methods.

Based on the foregoing, I concluded for myself that the widespread transition to the "elliptic" is not a necessity. In the end, while the usual RSA, DSA on the one hand, and GOST 34.10, ECDSA on the other, peacefully coexist, there is a false, but soothing sense of an alternative that we can lose by pursuing the most modern cryptographic methods.

Used Books

1. Don Johnson, Alfred Menezes, Scott Vanstone - The Elliptic Curve Digital Signature Algorithm.
2. A. Bolotov, S. Gashkov, A. Frolov, A. Chasovskikh - An elementary introduction to elliptic cryptography.
3. Lawrence Washington - Elliptic curves, Number theory and Cryptography.