June 20, 2013 at 22:20BINS-shmins. Introductory article
- Tutorial
- Recovery mode
It is registered on a habr from July 9, 2008. Never wrote anything, only read, Karma is below zero. Made up his mind.
Immediately an appeal to the respected “habrasociety” article is an attempt to sort out those issues that for me are still not completely understood, so I am waiting for constructive criticism and understandable feedback, and not “you're a fool and that’s all.” Now let's get down to the topic.
As the name will show, we will focus on the inertial navigation system. I studied at the Department of Robotics (2005-2011) and therefore the navigation problem for mobile robots was acute. For me it was always interesting how you can find out your coordinates and at the same time be independent of certain lighthouses, satellites and all kinds of sonars there. The answer appeared already in 2006, when I heard about a cool "gizmo" in the nokia n95 phone. At that time, an excursion for the "schoolchildren" would suddenly be read, these phones were very popular very well. In general, I learned about such a device as an accelerometer. Like it measures acceleration. But from physics and algebra, I knew that by taking the double integral you can find the displacement. I became terrified how interesting and I realized that I want to do this. Then of course I threw this idea in, because there was no way to feel the nokia n95 with an accelerometer, Then I became interested in artificial intelligence methods, image recognition tasks, etc. But a year before graduation, I came across some article about the Kalman filter and then surged again.
I wanted to write beautifully literary, but I feel not enough strength. I will not write about inertial navigation systems (ANN), in particular BINS (strapdown), there are a lot of articles on the Internet, and there are readable options on the hub. Just note, since mems sensors are getting cheaper, the SINS is growing in popularity. Thanks to the rapid development of interest in copters, I began to read literature and came across the term AHRS (Attitude and heading reference system), a translation from me “spatial position determination system” (SOPP). Very actively used in Western literature. And immediately the question arose of how it differs from ANN. My assumptions poured out in the following figure.
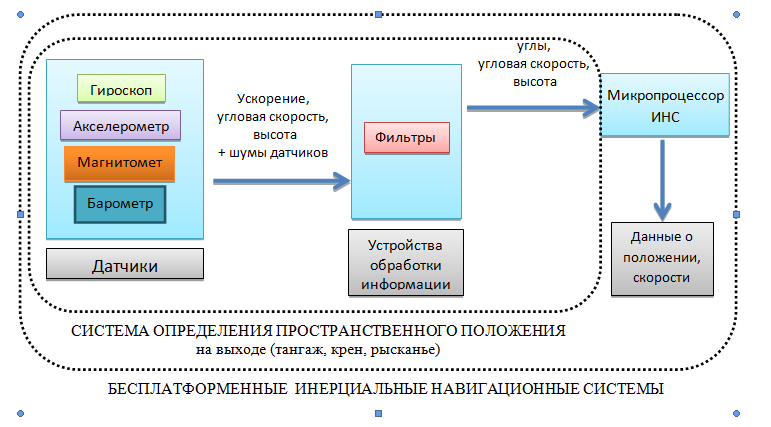
That is, SINS is a more “sophisticated option”, at the output of which there are coordinates about the position. Is this so and I ask your opinion in the comments.
The main sensors SINS can be considered an accelerometer and a gyroscope. The figure shows the main types of gyroscopes.
Figure taken from the book by V.Ya. Raspopova. If you want to understand the sensitive elements (SE) of inertial navigation, this is one of the best books. As for the accelerometer, here, by type, they are divided into three groups: macromechanical, micromechanical, integral. The accelerometer SE represents the inertial mass on the suspension. The macromechanical group includes accelerometers in which the suspension is implemented in the form of springs, strings or core, ball-bearing, electromagnetic units, which can also serve as measuring elements in so-called float accelerometers with hydrostatic unloading of suspension units. The antipode of macromechanical accelerometers is micromechanical in size, and integrated (hybrid) accelerometers are the product of the combined use of macro and MEMS technologies.
Drawing to represent the principle of work.
A strap-down ANN is being considered. In working and peasant terms, it will sound like this, the system does not have a physical real platform that remembers its state and protected the SE from the influence of the angular movements of the object. That is, in the case of SINS, gyroscopes and accelerometers are placed on the body of the object, and the onboard computing device performs the functions of the gyrostabilizing platform. This is a plus and the biggest minus of work. Since microcomputers must always be kept in memory transition matrices that always contain trigonometric functions. The task of the navigation system at the outputs is to give out the corners, the well-known names pitch, roll, yaw. Three methods of calculating these angles are common. The first is the simplest in terms of understanding the formulas and the implementation of the Euler-Krylov angles, the second method is very popular with the bourgeois, directing cosines (DCM) and the third with a slight tinge of "imaginary" quaternions or it is also called Rodrigue-Hamilton. In metamathematics and theory, the outputs of all three methods should be the same. The kinematic equations in the Euler – Krylov angles are of a low order (third) and have an understandable structure, but contain trigonometric functions of the desired angles and allow degeneration at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations. In metamathematics and theory, the outputs of all three methods should be the same. The kinematic equations in the Euler – Krylov angles are of a low order (third) and have an understandable structure, but contain trigonometric functions of the desired angles and allow degeneration at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations. In metamathematics and theory, the outputs of all three methods should be the same. The kinematic equations in the Euler – Krylov angles are of a low order (third) and have an understandable structure, but contain trigonometric functions of the desired angles and allow degeneration at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations. but they contain trigonometric functions of the desired angles and allow degeneracy at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations. but they contain trigonometric functions of the desired angles and allow degeneracy at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations.
Quaternions provide a convenient mathematical designation of the position and rotation of objects in space. Compared to Euler angles, quaternions make it easier to combine rotations, as well as to avoid the problem of the inability to rotate around an axis, regardless of perfect rotation along other axes (in the illustration). Compared to matrices, they are more computationally stable and can be more efficient.
I will give a generalized block diagram of the operation of the entire system as a whole.
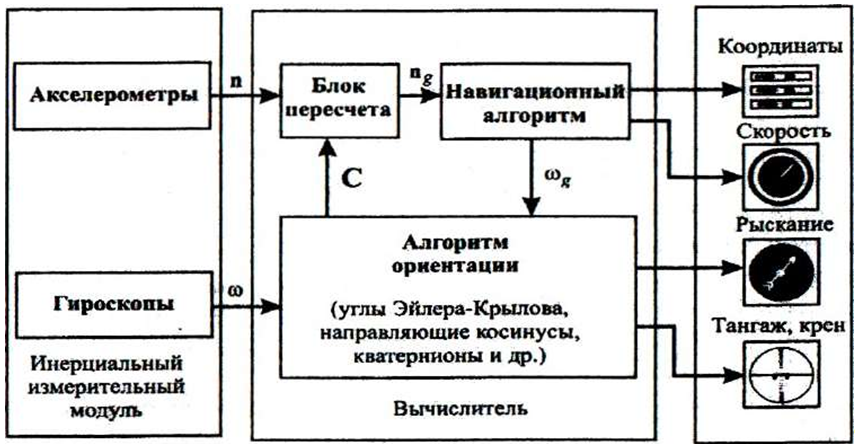. The drawing is taken from the book by Matveev, also a mastheva for binso researchers.
As mentioned above, the system needs to keep matrices with trigonometric functions in mind. Plus, at each step of calculating the value, we get an error, that is, we accumulate it. The second MEMS sensors, they have a lot of pluses, but they have a significant minus; they are “noisy”. That is, when designing a navigation system, you need to take into account the accumulation of errors and sensor noise. Here the question is whether I described all the problems. Now more about accumulating errors. For those who know higher mathematics excellent, they can skip. Here, as it were, thoughts aloud, this is where the error accumulates?
Take the sine. We considered him at school. No matter how. We remember its value for 3 angles and that’s it. And at the lessons of optics we were told that the sine at small angles is equal to the angle. That is, we knew three values for three "guest non-vital angles" and one sine for angles up to 5 degrees. But in life we are surrounded not only by angles equal to 30, 45 and 60 degrees. And there are 34, 79, and even with minutes and seconds. Then, the Bradis table came to our aid. That is, some calculation did not happen; we just looked in the table for a value or angle and that’s it. Then, those who have completed 2 semesters of the first year of those. Uni, learned about the Taylor series and numerical methods. In general, I’m why this is all, the microcontroller is not a person, it approaches the problem “recursively” “iteratively.” Taylor’s number, please, will count, but to someone, the sign and for some time. These "some" are very important. They, these uncertainties, contribute this very component of accumulation. Plus, the limitations of the computer itself in calculating the floating point number. The problems of integration and error accumulation in numerical methods are well described.here . I’ll still look for options for increasing accuracy in calculating trigonometry, but here, probably, everything depends on the programming language.
The second problem is a noisy signal from the sensors. Inertial navigation uses two methods of eliminating noise, the first filtering in the literal sense, the analogue “marlichka” which lets water through and does not let through everything else. And the second method, the "principle of redundancy", is when information about one state comes from several independent sources. A good article on this subject here .
My first article, in part, can be written in a primitive language, I just want it to be as clear as possible. Since the article is introductory, I want to figure out what specific issues the community is interested in. Now there is a ready-made article about modeling mems sensors in Maltab, I want to hear comments and comments on the first, I can make changes to the next article. There is experience and ready-made models of the entire navigation system (on DCM) in matlab. And there is a good project-continuation of a series of articles on cortex m3 / m4 on which it is all implemented.
Immediately an appeal to the respected “habrasociety” article is an attempt to sort out those issues that for me are still not completely understood, so I am waiting for constructive criticism and understandable feedback, and not “you're a fool and that’s all.” Now let's get down to the topic.
As the name will show, we will focus on the inertial navigation system. I studied at the Department of Robotics (2005-2011) and therefore the navigation problem for mobile robots was acute. For me it was always interesting how you can find out your coordinates and at the same time be independent of certain lighthouses, satellites and all kinds of sonars there. The answer appeared already in 2006, when I heard about a cool "gizmo" in the nokia n95 phone. At that time, an excursion for the "schoolchildren" would suddenly be read, these phones were very popular very well. In general, I learned about such a device as an accelerometer. Like it measures acceleration. But from physics and algebra, I knew that by taking the double integral you can find the displacement. I became terrified how interesting and I realized that I want to do this. Then of course I threw this idea in, because there was no way to feel the nokia n95 with an accelerometer, Then I became interested in artificial intelligence methods, image recognition tasks, etc. But a year before graduation, I came across some article about the Kalman filter and then surged again.
ANN or SOPP?
I wanted to write beautifully literary, but I feel not enough strength. I will not write about inertial navigation systems (ANN), in particular BINS (strapdown), there are a lot of articles on the Internet, and there are readable options on the hub. Just note, since mems sensors are getting cheaper, the SINS is growing in popularity. Thanks to the rapid development of interest in copters, I began to read literature and came across the term AHRS (Attitude and heading reference system), a translation from me “spatial position determination system” (SOPP). Very actively used in Western literature. And immediately the question arose of how it differs from ANN. My assumptions poured out in the following figure.
That is, SINS is a more “sophisticated option”, at the output of which there are coordinates about the position. Is this so and I ask your opinion in the comments.
Sensors, sensing elements.
The main sensors SINS can be considered an accelerometer and a gyroscope. The figure shows the main types of gyroscopes.
Figure taken from the book by V.Ya. Raspopova. If you want to understand the sensitive elements (SE) of inertial navigation, this is one of the best books. As for the accelerometer, here, by type, they are divided into three groups: macromechanical, micromechanical, integral. The accelerometer SE represents the inertial mass on the suspension. The macromechanical group includes accelerometers in which the suspension is implemented in the form of springs, strings or core, ball-bearing, electromagnetic units, which can also serve as measuring elements in so-called float accelerometers with hydrostatic unloading of suspension units. The antipode of macromechanical accelerometers is micromechanical in size, and integrated (hybrid) accelerometers are the product of the combined use of macro and MEMS technologies.
Drawing to represent the principle of work.Work algorithms
A strap-down ANN is being considered. In working and peasant terms, it will sound like this, the system does not have a physical real platform that remembers its state and protected the SE from the influence of the angular movements of the object. That is, in the case of SINS, gyroscopes and accelerometers are placed on the body of the object, and the onboard computing device performs the functions of the gyrostabilizing platform. This is a plus and the biggest minus of work. Since microcomputers must always be kept in memory transition matrices that always contain trigonometric functions. The task of the navigation system at the outputs is to give out the corners, the well-known names pitch, roll, yaw. Three methods of calculating these angles are common. The first is the simplest in terms of understanding the formulas and the implementation of the Euler-Krylov angles, the second method is very popular with the bourgeois, directing cosines (DCM) and the third with a slight tinge of "imaginary" quaternions or it is also called Rodrigue-Hamilton. In metamathematics and theory, the outputs of all three methods should be the same. The kinematic equations in the Euler – Krylov angles are of a low order (third) and have an understandable structure, but contain trigonometric functions of the desired angles and allow degeneration at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations. In metamathematics and theory, the outputs of all three methods should be the same. The kinematic equations in the Euler – Krylov angles are of a low order (third) and have an understandable structure, but contain trigonometric functions of the desired angles and allow degeneration at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations. In metamathematics and theory, the outputs of all three methods should be the same. The kinematic equations in the Euler – Krylov angles are of a low order (third) and have an understandable structure, but contain trigonometric functions of the desired angles and allow degeneration at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations. but they contain trigonometric functions of the desired angles and allow degeneracy at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations. but they contain trigonometric functions of the desired angles and allow degeneracy at a pitch angle of 90 °. All this determines their unsuitability in SINS. The SINS equations written using the matrix of guide cosines are linear, defined for any yaw, pitch, and roll angles, however, the equations are quite high - the ninth order. In addition, the equations must be supplemented by six coupling equations.
Quaternions provide a convenient mathematical designation of the position and rotation of objects in space. Compared to Euler angles, quaternions make it easier to combine rotations, as well as to avoid the problem of the inability to rotate around an axis, regardless of perfect rotation along other axes (in the illustration). Compared to matrices, they are more computationally stable and can be more efficient.
I will give a generalized block diagram of the operation of the entire system as a whole.
. The drawing is taken from the book by Matveev, also a mastheva for binso researchers.All problems binoculars
As mentioned above, the system needs to keep matrices with trigonometric functions in mind. Plus, at each step of calculating the value, we get an error, that is, we accumulate it. The second MEMS sensors, they have a lot of pluses, but they have a significant minus; they are “noisy”. That is, when designing a navigation system, you need to take into account the accumulation of errors and sensor noise. Here the question is whether I described all the problems. Now more about accumulating errors. For those who know higher mathematics excellent, they can skip. Here, as it were, thoughts aloud, this is where the error accumulates?
Take the sine. We considered him at school. No matter how. We remember its value for 3 angles and that’s it. And at the lessons of optics we were told that the sine at small angles is equal to the angle. That is, we knew three values for three "guest non-vital angles" and one sine for angles up to 5 degrees. But in life we are surrounded not only by angles equal to 30, 45 and 60 degrees. And there are 34, 79, and even with minutes and seconds. Then, the Bradis table came to our aid. That is, some calculation did not happen; we just looked in the table for a value or angle and that’s it. Then, those who have completed 2 semesters of the first year of those. Uni, learned about the Taylor series and numerical methods. In general, I’m why this is all, the microcontroller is not a person, it approaches the problem “recursively” “iteratively.” Taylor’s number, please, will count, but to someone, the sign and for some time. These "some" are very important. They, these uncertainties, contribute this very component of accumulation. Plus, the limitations of the computer itself in calculating the floating point number. The problems of integration and error accumulation in numerical methods are well described.here . I’ll still look for options for increasing accuracy in calculating trigonometry, but here, probably, everything depends on the programming language.
The second problem is a noisy signal from the sensors. Inertial navigation uses two methods of eliminating noise, the first filtering in the literal sense, the analogue “marlichka” which lets water through and does not let through everything else. And the second method, the "principle of redundancy", is when information about one state comes from several independent sources. A good article on this subject here .
Instead of conclusions
My first article, in part, can be written in a primitive language, I just want it to be as clear as possible. Since the article is introductory, I want to figure out what specific issues the community is interested in. Now there is a ready-made article about modeling mems sensors in Maltab, I want to hear comments and comments on the first, I can make changes to the next article. There is experience and ready-made models of the entire navigation system (on DCM) in matlab. And there is a good project-continuation of a series of articles on cortex m3 / m4 on which it is all implemented.