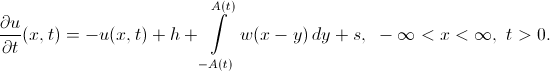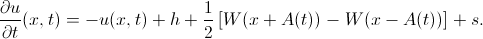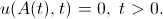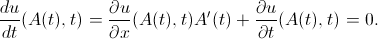An unusual way to generate mazes

In this article, I will talk about one unusual approach to generating mazes. It is based on the model of Amary neuronal activity of the cerebral cortex, which is a continuous analogue of neural networks. Under certain conditions, it allows you to create beautiful labyrinths of a very complex shape, similar to what is shown in the picture.

You will find a lot of analysis and some private derivatives. The code is attached.
I ask for a cut!

Introduction

Many readers have already faced the problem of generating a maze in one form or another and know that to solve it, they often use the Prima and Kruskal algorithms to find the minimum spanning tree in a graph whose vertices are the cells of the maze and the edges represent the passages between adjacent cells. We will take a bold step away from graph theory towards ... computational neurobiology.

During the 20th century, scientists built mathematical models of single neurons (cells of the nervous system) and their interactions. In 1975, S. Amari introduced the light of his continuous model of the cerebral cortex. In it, the nervous system was considered as a continuous medium, at each point of which there is a "neuron", characterized by the value of the potential of its membrane, which changes its potential by exchanging charges with neighboring neurons and external stimuli. Amari's model is famous for explaining many phenomena of human vision and, in particular, visual hallucinations caused by psychoactive substances.

The Amari model, in its simplest form, is the Cauchy problem for one integro-differential equation:

Here you can not do without explanation:

• - the real value of the potential of the membrane of a neuron at a point in time .
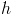• - rest potential (some material constant).
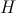• - Heaviside step function:

  

• - weight function.
• - external irritant.
• - distribution of potential at the initial moment of time.
• Is an arbitrary point of the region on which the potential is determined. Since we plan to generate a two-dimensional image of the labyrinth, we will consider the entire material plane as.
• The partial 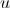time derivative on the left side denotes an instantaneous change in potential 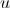. The right part sets the rule for this change.
• The first two terms on the right side mean that, in the absence of stimuli, the potential value tends to the value of the resting potential.
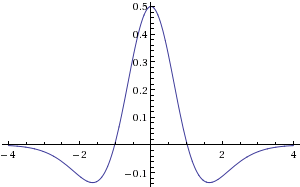
• The following term takes into account the effects of neighboring neurons. The Heaviside function plays the role of the activation function of a neuron: a neuron begins to influence its neighbors only if its potential is greater than zero. We will further call such neurons active, and the set of points with positive potential is called the area of ​​activity. It is clear that resting neurons should not be active, that is, the resting potential should not be positive. Active neighbors can be divided into two groups: excitatory and inhibitory. Exciting neurons increase the potential of neighbors, and inhibitory neurons decrease. At the same time, exciters create a powerful burst of activity in a small neighborhood, while inhibitory ones gradually extinguish activity in the vicinity of a large radius. This fact is reflected in the choice of the weight function in the form of a “Mexican hat”:

  
  

• The last term on the right side of the equation takes into account the action of an external stimulus. For example, for the visual cortex of the brain, the signal received from the retina of the eye is a natural stimulus. We assume that the stimulus is given by a non-negative stationary (time-independent) function.

We ask ourselves a question: is it possible to select the model parameters 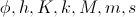so that its stationary solution (at ) is an image of some maze?

Amari Model Solutions Properties

To analyze the solutions of the Amari model, it will suffice for us to confine ourselves to considering the one-dimensional case. For simplicity, we assume that it is constant on the whole line.
First of all, we are interested in the so-called bump solutions. They are remarkable in that they are positive only on some finite interval with moving boundaries. Amari equation for them is written as follows:

To understand how its solution behaves, we introduce the function

Now the same equation can be rewritten as follows:

We know that the bump solution vanishes at the boundaries of the activity interval (that’s why they are called boundaries). We write this condition on the right boundary:

Now we differentiate the last identity with respect to the variable :

From here:

Substituting the last expression in the equation for the bump solution with 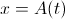, we obtain:

Now we note that the partial derivative with respect to the left-hand side is always negative, since the solution to the left of the right boundary is greater than zero, and to the right of it, less. therefore

Thus, the direction of the shift of the boundary depends only on the value of the expression on the right side. If it is greater than zero, then the area of ​​activity expands; if less, it narrows. If zero, equilibrium is reached.
Take a look at the possible function graphs .

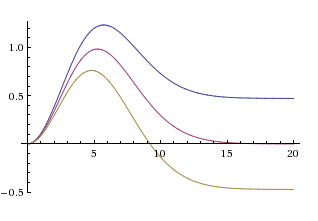
Obviously, two cases are possible:

1. The limit value is non-negative. Then the area of ​​activity of the bump solution will expand unlimitedly.
2. The limit value is negative. Then the area of ​​activity will be limited. Moreover, in this case it can be shown that the connected components of the region of activity of the solution to the Amari equation never merge .

Unfortunately, in the two-dimensional case , it is difficult to obtain an explicit expression for the function , so we simply evaluate it:

From here:

Maze generation

Having collected the luggage of the necessary knowledge, we can begin, in fact, the algorithm for generating the maze.
First of all, we will decide on the very concept of “labyrinth”. By a maze we mean a binary function such that the region 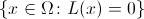is connected. A value of 0 corresponds to a free cell, and a value of 1 corresponds to an impenetrable wall. The condition of connectivity suggests that from any free cell you can get to any other without destroying the walls. We will search for the function in the form:

where 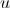is the solution to the Amari model. It remains only to determine the parameters of the model.
To begin with, we fix an arbitrary negative value 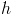. Naturally put 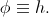. Now let's define a function . Let its value at each point be determined by a random variable uniformly distributed over a segment . In this case, the stimulus will not create activity. We fix an arbitrary positive . This parameter affects only the absolute value of the potential, therefore it is not of interest. We fix arbitrary positive ones 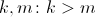. They determine the characteristic wall thickness of the maze. We will try to determine the parameter experimentally, and then compare it with the theoretical estimate obtained in the previous section.
We will seek a stationary solution by the method of successive approximations:

And here’s the long awaited interactive demo in Python:

import math
import numpy
import pygame
from scipy.misc import imsave
from scipy.ndimage.filters import gaussian_filter
class AmariModel(object):
    def __init__(self, size):
        self.h = -0.1
        self.k = 0.05
        self.K = 0.125
        self.m = 0.025
        self.M = 0.065
        self.stimulus = -self.h * numpy.random.random(size)
        self.activity = numpy.zeros(size) + self.h
        self.excitement = numpy.zeros(size)
        self.inhibition = numpy.zeros(size)
    def stimulate(self):
        self.activity[:, :] = self.activity > 0
        sigma = 1 / math.sqrt(2 * self.k)
        gaussian_filter(self.activity, sigma, 0, self.excitement, "wrap")
        self.excitement *= self.K * math.pi / self.k
        sigma = 1 / math.sqrt(2 * self.m)
        gaussian_filter(self.activity, sigma, 0, self.inhibition, "wrap")
        self.inhibition *= self.M * math.pi / self.m
        self.activity[:, :] = self.h
        self.activity[:, :] += self.excitement
        self.activity[:, :] -= self.inhibition
        self.activity[:, :] += self.stimulus
class AmariMazeGenerator(object):
    def __init__(self, size):
        self.model = AmariModel(size)
        pygame.init()
        self.display = pygame.display.set_mode(size, 0)
        pygame.display.set_caption("Amari Maze Generator")
    def run(self):
        pixels = pygame.surfarray.pixels3d(self.display)
        index = 0
        running = True
        while running:
            self.model.stimulate()
            pixels[:, :, :] = (255 * (self.model.activity > 0))[:, :, None]
            pygame.display.flip()
            for event in pygame.event.get():
                if event.type == pygame.QUIT:
                    running = False
                elif event.type == pygame.KEYDOWN:
                    if event.key == pygame.K_ESCAPE:
                        running = False
                    elif event.key == pygame.K_s:
                        imsave("{0:04d}.png".format(index), pixels[:, :, 0])
                        index = index + 1
                elif event.type == pygame.MOUSEBUTTONDOWN:
                    position = pygame.mouse.get_pos()
                    self.model.activity[position] = 1
        pygame.quit()
def main():
    generator = AmariMazeGenerator((512, 512))
    generator.run()
if __name__ == "__main__":
    main()

I think the comments are superfluous. I would like to note only that the convolution with the weight function is calculated through a Gaussian filter, and the images continue periodically to the entire plane (the “wrap” parameter). The demonstration is interactive in the sense that it allows you to forcibly establish a positive potential at any point by click.
The behavior of the solution, as expected, depends on the choice of parameter :

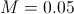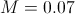Now we get a theoretical estimate of the optimal parameter value . It satisfies the condition:

Therefore, it can be estimated as follows:

Not bad, but the real value is slightly higher than the theoretical estimate. This is easy to verify by putting .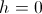

Finally, you can change the degree of "sparseness" of the maze by changing the value of the parameter :

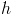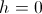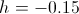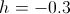Conclusion

So we finished the discussion, perhaps, of the most extraordinary way of generating labyrinths. I hope you found the article interesting. In conclusion, I will provide a list of literature for those wishing to broaden their horizons:

[1] Konstantin Doubrovinski, Dynamics, Stability and Bifurcation Phenomena in the Nonlocal Model of Cortical Activity , 2005.
[2] Dequan Jin, Dong Liang, Jigen Peng, Existence and Properties of Stationary Solution of Dynamical Neural Field , 2011.
[3] Stephen Coombes, Helmut Schmidt, Ingo Bojak, Interface Dynamics in Planar Neural Field Models , 2012.