Cutting into two equal parts, part three
The first part
The first part of the second part
The second part of the second part
Well, gentlemen, it's time to finish. In the last article of the cycle (the name of which breaks my template that hasn’t really woken up yet), we will put a bullet in the history of this task. Despite the fact that in the comments to the second part a more convenient and universal way was suggested to do this, I will still use the tools that I personally developed before writing the first of the articles. Firstly, goodness is not to be lost, and secondly, I think everyone understands that the task is just an excuse to draw beautiful drawings in GeoGebra and post them to the hub Well, as they say, it started.
Sliding symmetry is determined by the following parameters: the axis of symmetry and the shear vector parallel to it. The axis of symmetry, in turn, is determined by the direction and specific position on the plane. Now I will outline a number of facts following from each other, obvious enough not to even call them lemmas, and even less to prove.
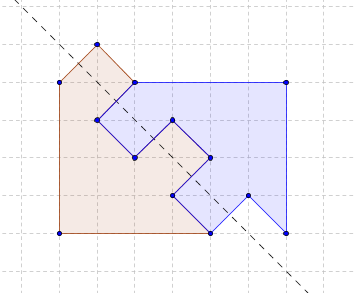
Armed with these facts, I drew this picture:

From it it is clear that for most directions at the borders there will be either points A and E, or points B and F, and therefore, the axis will go through the "center" of the figure (the intersection of the diagonals of the rectangle ABEF). The second place in prevalence is occupied by the case with points C and F, the honorable third - with points C and A. In these cases, obviously, the axis of symmetry will pass through the midpoints of the segments CF and CA, respectively.
Now let's see in what directions the axis will divide the figure into two equal parts. Without going into tedious details, I’ll say simply: but with such.
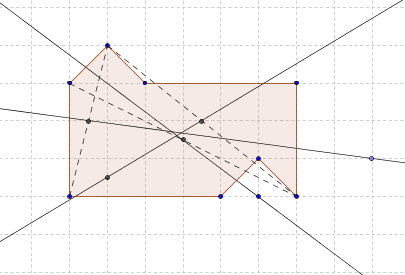
Now we have three specific axes and, moreover, three specific shift vectors are attached to them - because the boundaries in all cases consist of one point. It is easy to show that for all these three moving symmetries, there are points of the figure for which there is neither an image nor an inverse image - which, according to Lemma 3, means that these are bad, worthless moving symmetries that cannot correspond to splitting the figure into two equal parts. I leave the search for specific points to the reader.
Figure A 0 cannot be cut into two equal parts. Now I will go with a clear conscience to revise "And the dawns here are quiet." Happy Victory Day, comrades Khabrovites.
The first part of the second part
The second part of the second part
Well, gentlemen, it's time to finish. In the last article of the cycle (the name of which breaks my template that hasn’t really woken up yet), we will put a bullet in the history of this task. Despite the fact that in the comments to the second part a more convenient and universal way was suggested to do this, I will still use the tools that I personally developed before writing the first of the articles. Firstly, goodness is not to be lost, and secondly, I think everyone understands that the task is just an excuse to draw beautiful drawings in GeoGebra and post them to the hub Well, as they say, it started.

Case 3: Moving Symmetry
Sliding symmetry is determined by the following parameters: the axis of symmetry and the shear vector parallel to it. The axis of symmetry, in turn, is determined by the direction and specific position on the plane. Now I will outline a number of facts following from each other, obvious enough not to even call them lemmas, and even less to prove.
- The axis of moving symmetry is equidistant from the boundaries (we take the concept of the boundary non-selectively from the case of parallel transfer).
- If we take a segment with ends at different boundaries, then the axis of symmetry will pass through its middle.
- By setting the direction of the axis of moving symmetry, we automatically know its specific position. If both boundaries consist of a single point, then we also know the shift vector.
- The parts into which the figure is divided by the axis have an equal area (this fact does not follow from the previous ones)
Armed with these facts, I drew this picture:

From it it is clear that for most directions at the borders there will be either points A and E, or points B and F, and therefore, the axis will go through the "center" of the figure (the intersection of the diagonals of the rectangle ABEF). The second place in prevalence is occupied by the case with points C and F, the honorable third - with points C and A. In these cases, obviously, the axis of symmetry will pass through the midpoints of the segments CF and CA, respectively.
Now let's see in what directions the axis will divide the figure into two equal parts. Without going into tedious details, I’ll say simply: but with such.

Now we have three specific axes and, moreover, three specific shift vectors are attached to them - because the boundaries in all cases consist of one point. It is easy to show that for all these three moving symmetries, there are points of the figure for which there is neither an image nor an inverse image - which, according to Lemma 3, means that these are bad, worthless moving symmetries that cannot correspond to splitting the figure into two equal parts. I leave the search for specific points to the reader.
Conclusion
Figure A 0 cannot be cut into two equal parts. Now I will go with a clear conscience to revise "And the dawns here are quiet." Happy Victory Day, comrades Khabrovites.
