Numerical methods for solving elliptic equations
Introduction
The most common elliptic equation is the Poisson equation.
Many problems of mathematical physics, such as the problem of stationary temperature distribution in a solid, diffusion problems, the distribution of an electrostatic field in a nonconducting medium in the presence of electric charges, and many others, are reduced to solving this equation.
In the case of several measurements, numerical methods are used to solve elliptic equations, which allow transforming differential equations or their systems into systems of algebraic equations. The accuracy of the solution is determined by the grid spacing, the number of iterations and the computer bit grid [1].
The purpose of the publication.obtain the solution of the Poisson equation for the Dirichlet and Neumann boundary conditions; investigate the convergence of the relaxation solution method using examples.
The Poisson equation refers to equations of the elliptic type and in the one-dimensional case has the form [1]:
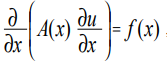 (1)
(1) where x is the coordinate; u (x) is the desired function; A (x), f (x) are some continuous coordinate functions.
We solve the one-dimensional Poisson equation for the case A = 1, which in this case takes the form:
 (2)
(2) Let us set a uniform coordinate grid with step Δх on the interval [xmin, xmax]:
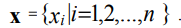 (3) The
(3) The boundary conditions of the first kind (Dirichlet conditions) for the problem under consideration can be represented as:
 (4)
(4) where x1, xn are the coordinates of the boundary points of the region [xmin, xmax]; g1, g2 are some
constants.
The boundary conditions of the second kind (Neumann conditions) for the problem in question can be represented as:
 (5)
(5)Carrying out the discretization of Dirichlet boundary conditions on a uniform grid (3) using the finite difference method, we obtain:
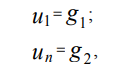 (6)
(6) where u1, un are the values of the function u (x) at the points x1 and xn, respectively.
Carrying out discretization of Neumann boundary conditions on the grid (3), we obtain:
 (7)
(7) Carrying out discretization of equation (2) for internal grid points, we get:
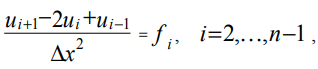 (8)
(8) where ui, fi are the values of the functions u (x), f (x) at the point grids with xi coordinate.
Thus, as a result of discretization, we obtain a system of linear algebraic equations of dimension n, containing n - 2 equations of the form (8) for interior points of the domain and equations (6) and (7) for two boundary points [1].
Below is a Python listing of the numerical solution of equation (2) with boundary conditions (4) - (5) on a coordinate grid (3).
Solution listing
from numpy import*
from numpy.linalg import solve
import matplotlib.pyplot as plt
x0=0#Начальная координата области решения
xn=5#Конечная координата области решения
n=100#Число точек координатной сетки
dx=(xn-x0)/(n-1)#Задание равномерной координатной сетки с шагом dx
x=[i*dx+x0 for i in arange(0,n,1)]#Задание равномерной координатной сетки с шагом dxdeff(i):#Функция правой части уравненияreturn2*sin(x[i]**2)+cos(x[i]**2)
v1=1.0#Вид ГУ на левой границе (1 - Дирихле, 2 - Неймана)
g1=0.0#Значение ГУ на левой границе
v2=2.0#'Вид ГУ на правой границе (1 - Дирихле, 2 - Неймана)
g2=-0.5#Значение ГУ на правой границе
a=zeros([n,n])#Задание матрицы коэффициентов СЛАУ размерностью n x n
b=zeros([1,n])# Задание матрицы-строки свободных членов СЛАУ размерностью 1 x n#Определение коэффициентов и свободных членов СЛАУ,# соответствующих граничным условиям и проверка корректности#значений параметров v1, v2
b[0,n-1]=g1;
if v1==1:
a[0,0]=1elif v1==2:
a[0,0]=-1/dx
a[0,1]=1/dx;
else:
print('Параметр v1 имеет неправильное значение')
b[0,n-1]=g2;
if v2==1:
a[n-1,n-1]=1elif v2==2:
a[n-1,n-1]=1/dx
a[n-1,n-2]=-1/dx;
else:
print('Параметр v2 имеет неправильное значение')
#Определение коэффициентов и свободных членов СЛАУ,# соответствующих внутренним точкам области for i in arange(1, n-1,1):
a[i,i]=-2/dx**2
a[i,i+1]=1/dx**2
a[i,i-1]=1/dx**2
b[0,i]=f(i)
u=linalg.solve(a,b.T).T#Решение СЛАУdefviz(v1,v2):if v1==v2==1:
return"ГУ Дирихле на левой и ГУ Дирихле на правой границе "elif v1==1and v2==2:
return"ГУ Дирихле на левой и ГУ Неймана на правой границе "elif v2==1and v2==1:
return"ГУ Неймана на левой и ГУ Дирихле на правой границе "
plt.figure()
plt.title("График функции правой части уравнения Пуассона")
y=[f(i) for i in arange(0,n,1)]
plt.plot(x,y)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.figure()
plt.title("График искомой функции уравнения Пуассона")
plt.xlabel('x')
plt.ylabel('u(x)')
plt.plot(x,u[0,:],label='%s'%viz(v1,v2))
plt.legend(loc='best')
plt.grid(True)
plt.show()We get:


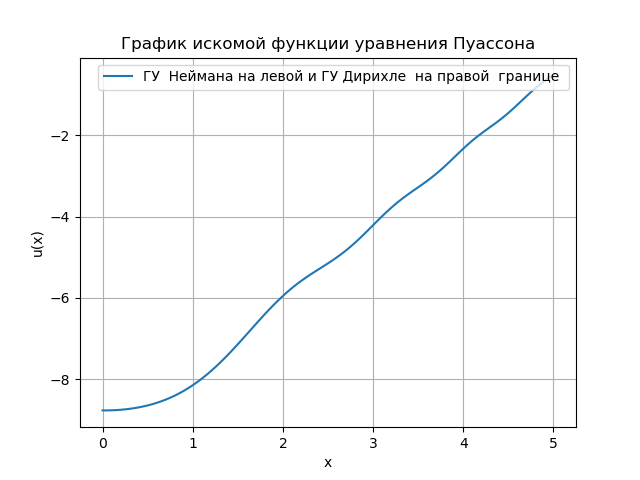

The program I developed in Python is convenient for analyzing boundary conditions. The reduced Python solution algorithm uses the Numpy function - u = linalg.solve (a, bT) .T to solve a system of algebraic equations, which improves the speed with a square matrix {a}. However, with an increase in the number of measurements, it is necessary to switch to the use of a three diagonal matrix, a solution for which becomes even more complicated for a very simple task. I found an example on the forum:
An example of a solution with a three-diagonal matrix
from __future__ import print_function
from __future__ import division
import numpy as np
import time
ti = time.clock()
m = 1000
A = np.zeros((m, m))
B = np.zeros((m, 1))
A[0, 0] = 1
A[0, 1] = 2
B[0, 0] = 1for i in range(1, m-1):
A[i, i-1] = 7
A[i, i] = 8
A[i, i+1] = 9
B[i, 0] = 2
A[m-1, m-2] = 3
A[m-1, m-1] = 4
B[m-1, 0] = 3
print('A \n', A)
print('B \n', B)
x = np.linalg.solve(A, B) # solve A*x = B for x
print('x \n', x)
print('NUMPY time', time.clock()-ti, 'seconds') The program of numerical solution on the Dirichlet problem uniform for each direction of the grid for the convection-diffusion equation
[2] (9)
(9) We use approximations by central differences for the convective term and an iterative relaxation method. For the dependence of the rate of convergence on the relaxation parameter when the problem with / (x) = 1 and 6 (x) = 0.10 is solved numerically. In the grid problem:
 (10)
(10) Let us represent matrix A as a sum of diagonal, lower triangular and upper triangular matrices:
 (10)
(10) The relaxation method corresponds to the use of an iterative method :
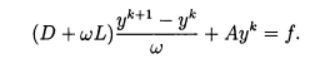 (11)
(11) When
 \ speak of upper relaxation, with
\ speak of upper relaxation, with 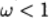 - lower relaxation.
- lower relaxation.Program Listing
from numpy import *
""" Численное решение задачи Дирихле
для уравнения конвекции-диффузии в
прямоугольнике.Метод релаксации."""defrelaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8):
h1 = I1 / n1
h2 = I2 / n2
d = 2. / h1**2 + 2. / h2**2
y = zeros([n1+1, n2+1])
ff = zeros([n1+1, n2+1])
bb = zeros([n1+1, n2+1])
for j in arange(1,n2,1):
for i in arange(1,n1,1):
ff [i,j] = f(i*h1, j*h2)
bb[i,j] = b(i*h1, j*h2)
#максимальное число итераций - 10000for k in arange(1, 10001,1):
rn = 0.for j in arange(1,n2,1):
for i in arange(1,n1,1):
rr = - (y[i-1,j] - 2.*y [i, j] + y[i+1,j]) / h1**2 \
- (y[i,j-1] - 2.*y [i,j] + y[i,j+1]) / h2**2 \
+ bb[i,j]*(y [i+1,j] - y [i-1,j]) / (2.*h1) - ff [i,j]
rn = rn + rr**2
y[i,j] = y[i,j] - omega * rr / d
rn = rn*h1*h2
if rn < tol**2: return y, k
print ('Метод релаксации не сходиться:')
print ('после 10000 итерации остаток=',sqrt(rn))
import matplotlib.pyplot as plt
bcList = [0., 10.]
sglist = ['-','--']
kk = 0for bc in bcList:
I1 = 1.
I2 = 1.deff(x,y):return1.defb(x,y):return bc
n1 = 25
n2 = 25
m = 20
om = linspace(1., 1.95, m)
it = zeros(([m]))
for k in arange(0,m,1):
omega = om[k]
y, iter = relaxation(b, f, I1, I2, n1, n2, omega, tol=1.e-6)
it[k] = iter
s1= 'b =' + str(bc)
sg = sglist[kk]
kk = kk+1
plt.plot( om,it, sg, label = s1)
plt.title("Число итераций метода релаксации\n для приближённого решения эллиптической задачи\n с использованием заданного параметра релаксации $\\omega$")
plt.xlabel('$\\omega$')
plt.ylabel('iterations')
plt.legend(loc=0)
plt.grid(True)
plt.show(We obtain:
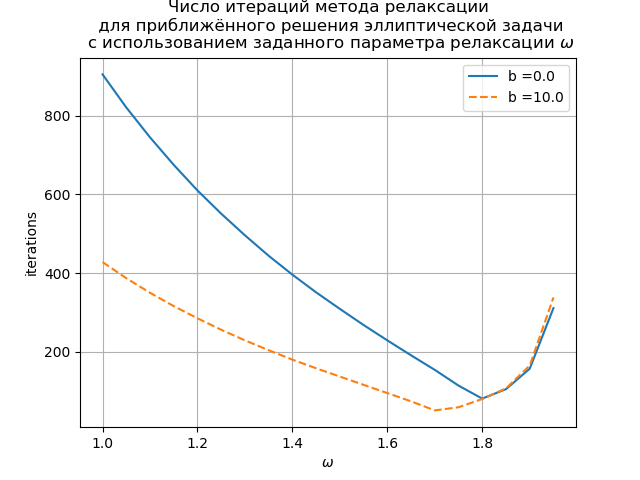
The graph shows the dependence of the number of iterations on the relaxation parameter for the Poisson equation (b (x) = 0) and the convection-diffusion equation (b (x) = 10). For the grid Poisson equation, the optimal value of the relaxation parameter is found analytically, and the iterative method converges at
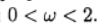 .
. Findings:
- The solution of an elliptic problem in Python with a flexible system for setting boundary conditions is given.
- It is shown that the relaxation method has an optimal range (
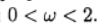 ) of the relaxation parameter.
) of the relaxation parameter.
References:
- Ryndin E.A. Methods for solving problems of mathematical physics. - Taganrog:
Publishing house of TSURE, 2003. - 120 p. - Vabishchevich PN. Numerical methods: Computational practical work. - M .: Book House
"LIBROCOM", 2010. - 320 p.
