How arrays are arranged in PHP
In the last article I talked about variables, now we will talk about arrays.
At the PHP level, an array is an ordered list crossed with map. Roughly speaking, PHP mixes these two concepts; as a result, it turns out, on the one hand, a very flexible data structure, on the other hand, perhaps not the most optimal, more precisely, as Anthony Ferrara put it:

(the picture depicts a HashTable with Bucket, V. Vasnetsov)
And here's the beginning - let's try to measure the memory and time consumed by each inserted value. We will do this using the following scripts:
We run these scripts
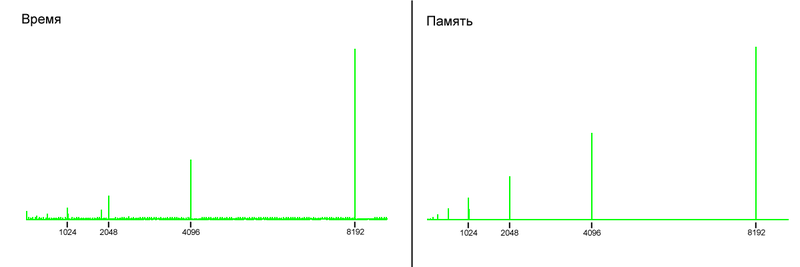
(on the X axis - the number of el-ets in the array)
As you can see, on both graphs there are jumps both in consumed memory and in used time, and these jumps occur at the same moments.
The fact is that at the C level (and indeed at the system level), there are no arrays with non-fixed size. Each time you create an array in C, you must specify its size so that the system knows how much memory you need to allocate to it.
Then how is this implemented in PHP and how to compile those jumps on the chart?
When you create an empty array, PHP creates it with a specific size. If you fill the array and at one point you reach and exceed this size, then a new array with twice the size is created, all elements are copied into it and the old array is destroyed. Generally, this is a standard approach.
In fact, to implement arrays in PHP, we use a completely standard Hash Table data structure , which we will talk about the implementation details.
The Hash Table stores a pointer to the very first and last value (needed to arrange the arrays), a pointer to the current value (used to iterate over the array, this is what returns
Why
There are two main entities in the Hash Table, the first is the Hash Table itself, and the second is the Bucket (hereinafter bucket, so as not to get bored).
The buckets themselves store the values, that is, each value has its own bucket. But besides this, the original key is stored in the bucket, pointers to the next and previous buckets (they are needed to arrange the array, because in PHP the keys can go in any order you want), and, again, something else.
Thus, when you add a new element to the array, if there is no such key there, then a new bucket is created under it and added to the Hash Table.
But the most interesting thing is how these buckets are stored in the Hash Table.
As mentioned above, HT has a certain array of pointers to buckets, while buckets are available in this array at a certain index, and this index can be calculated by knowing the key of the bucket. It sounds a little complicated, but in fact, everything is much simpler than it sounds. Let's try to parse how an item is obtained by key from HT:
About the mask: let's say the array of pointers contains 4 elements, so the mask is three, that is 11 in the binary system.
Now, if we get a number like 123 (1111011) as a key, then after masking we get 3 (3 & 123), this number can already be used as an index.
After that, we will try to add elements with keys 54 and 90 to the Hash Table, with mask 3. And both of these keys will be equal to two after masking.
The buckets turn out to have a couple more cards in their sleeves. Each bucket also has a pointer to the previous and next bucket, for which the indices (hashes from the keys) are equal.
Thus, in addition to the main doubly linked list that runs between all buckets, there are also small doubly linked lists between those buckets whose indices are equal. That is, we get the following picture:

Let's go back to our case with keys 54 and 90, and mask 3. After you add 54, the HT structure will look something like this:
Now add an element with a key of 90, now everything will look something like this:
Now let's add some elements before the nTableSize overflow (I remind you that the overflow will only happen when nNumOfElements> nTableSize).
Add elements with keys 0, 1, 3 (those that were not there, and after applying the masks they will remain the same), this is what will happen:
What happens after the array overflows is called rehash. Essentially, iterating over all existing buckets (via pListNext), assigning their neighbors (collisions), and adding references to them in arBuckets.
But what actually happens when an element is received by key? Something else will be added to the previous algorithm:
So until either the buckets in pNext run out (then Notice will be thrown), or until a match is found.
It is worth noting that in PHP almost everything is built on this HashTable structure alone: all variables lying in any scope actually lie in HT, all class methods, all class fields, even class definitions themselves, lie in HT, it is actually a very flexible structure. Among other things, HT provides almost the same speed of fetching / inserting / deleting and the complexity of all three is O (1), but with the caveat for a small overhead in case of collisions.
By the way, here I implemented a Hash Table in PHP itself. Well, that is, implemented PHP arrays in PHP =)
What are arrays at the PHP level?
At the PHP level, an array is an ordered list crossed with map. Roughly speaking, PHP mixes these two concepts; as a result, it turns out, on the one hand, a very flexible data structure, on the other hand, perhaps not the most optimal, more precisely, as Anthony Ferrara put it:
PHP arrays are a great one-size-fits-all data structure. But like all one-size-fits-all, jack-of-all-trades usually means master of none.
Link to the letter

(the picture depicts a HashTable with Bucket, V. Vasnetsov)
And here's the beginning - let's try to measure the memory and time consumed by each inserted value. We will do this using the following scripts:
// time.php
$ar = array();
$t = 0;
for ($i = 0; $i < 9000; ++$i) {
$t = microtime(1);
$ar[] = 1;
echo $i . ":" . (int)((microtime(1) - $t) * 100000000) . "\n";
}
// memory.php
$ar = array();
$m = 0;
for ($i = 0; $i < 9000; ++$i) {
$m = memory_get_usage();
$ar[] = 1;
echo $i . ":" . (memory_get_usage() - $m) . "\n";
}
We run these scripts
php time.php > timeand php memory.php > memory, and draw graphs on them, because there is a lot of data and look at the numbers for a long time (time data were collected many times and aligned to avoid unnecessary jumps on the graph). 
(on the X axis - the number of el-ets in the array)
As you can see, on both graphs there are jumps both in consumed memory and in used time, and these jumps occur at the same moments.
The fact is that at the C level (and indeed at the system level), there are no arrays with non-fixed size. Each time you create an array in C, you must specify its size so that the system knows how much memory you need to allocate to it.
Then how is this implemented in PHP and how to compile those jumps on the chart?
When you create an empty array, PHP creates it with a specific size. If you fill the array and at one point you reach and exceed this size, then a new array with twice the size is created, all elements are copied into it and the old array is destroyed. Generally, this is a standard approach.
And how is this implemented?
In fact, to implement arrays in PHP, we use a completely standard Hash Table data structure , which we will talk about the implementation details.
The Hash Table stores a pointer to the very first and last value (needed to arrange the arrays), a pointer to the current value (used to iterate over the array, this is what returns
current()), the number of elements represented in the array, an array of pointers to Bucket (about them further), and one more thing.Why
do we
need buckets
and where
do we
put them
There are two main entities in the Hash Table, the first is the Hash Table itself, and the second is the Bucket (hereinafter bucket, so as not to get bored).
The buckets themselves store the values, that is, each value has its own bucket. But besides this, the original key is stored in the bucket, pointers to the next and previous buckets (they are needed to arrange the array, because in PHP the keys can go in any order you want), and, again, something else.
Thus, when you add a new element to the array, if there is no such key there, then a new bucket is created under it and added to the Hash Table.
But the most interesting thing is how these buckets are stored in the Hash Table.
As mentioned above, HT has a certain array of pointers to buckets, while buckets are available in this array at a certain index, and this index can be calculated by knowing the key of the bucket. It sounds a little complicated, but in fact, everything is much simpler than it sounds. Let's try to parse how an item is obtained by key from HT:
- If the key is string, then the string is hashed to integer-a (the DJBX33A hash algorithm is used):
- The original value of the hash is taken as magic 5381
- For each key symbol, multiply the hash by 33 and add the character number in ASCII
- A mask (bitwise and) is always applied to the resulting numeric key, which is always equal to the size of the array (which is with buckets) minus 1
- As a result, this key can be used as an index to get the desired pointer to the Bucket from the array
About the mask: let's say the array of pointers contains 4 elements, so the mask is three, that is 11 in the binary system.
Now, if we get a number like 123 (1111011) as a key, then after masking we get 3 (3 & 123), this number can already be used as an index.
After that, we will try to add elements with keys 54 and 90 to the Hash Table, with mask 3. And both of these keys will be equal to two after masking.
What to do with collisions?
The buckets turn out to have a couple more cards in their sleeves. Each bucket also has a pointer to the previous and next bucket, for which the indices (hashes from the keys) are equal.
Thus, in addition to the main doubly linked list that runs between all buckets, there are also small doubly linked lists between those buckets whose indices are equal. That is, we get the following picture:

Let's go back to our case with keys 54 and 90, and mask 3. After you add 54, the HT structure will look something like this:
{
nTableSize: 4, // размер массива указателей на ведра
nTableMask: 3, // маска
nNumOfElements: 1, // число элементов в HT
nNextFreeElement: 55, // это будет использовано тогда, когда вы захотите добавить элемент в конец массива (без ключа)
...,
arBuckets: [
NULL,
NULL,
0xff0, // представим, что это указатель на Bucket, а сам он описан ниже
NULL
]
}
0xff0: {
h: 54, // числовой ключ
nKeyLength: 0, // это длина ключа, в случае когда он строковый
pData: 0xff1, // указатель на значение, в данном случае на структуру zval
...
}
Now add an element with a key of 90, now everything will look something like this:
{
nTableSize: 4,
nTableMask: 3,
nNumOfElements: 2,
nNextFreeElement: 91,
...,
arBuckets: [
NULL,
NULL,
0xff0, // здесь все так же всего один Bucket
NULL
]
}
0xff0: {
h: 54,
pListNext: 0xff2, // здесь хранится указатель на следующий Bucket по порядку (для итерирования)
pNext: 0xff2, // а сюда попал новый Bucket с таким же хешем
...
}
0xff2: {
h: 90,
pListLast: 0xff0, // это предыдущий элемент
pLast: 0xff0, // а это тот же предыдущий элемент
...
}
Now let's add some elements before the nTableSize overflow (I remind you that the overflow will only happen when nNumOfElements> nTableSize).
Add elements with keys 0, 1, 3 (those that were not there, and after applying the masks they will remain the same), this is what will happen:
{
nTableSize: 8, // теперь размер вдвое больше (прям как в той рекламе)
nTableMask: 7,
nNumOfElements: 5,
nNextFreeElement: 91, // это число осталось неизменным
...,
arBuckets: [ // теперь некоторые ведра переместились на новые места, с учетом новой маски и следовательного нового индекса
0xff3, // key = 0
0xff4, // key = 1
0xff2, // key = 90 - теперь здесь сидит ключ 90 (его индекс 90 & 7 = 2), а его бывший сосед съехал на 6-й индекс
0xff5, // key = 3
NULL,
NULL,
0xff0, // key = 54
NULL
]
}
0xff0: {
h: 54,
pListNext: 0xff2, // порядок остался тот же, поэтому это значение неизменно
pNext: NULL, // а здесь теперь ничего
...
}
0xff2: {
h: 90,
pListNext: 0xff3,
pListLast: 0xff0,
pLast: NULL,
...
}
0xff3: {
h: 0,
pListNext: 0xff4,
pListLast: 0xff2,
...
}
0xff4: {
h: 1,
pListNext: 0xff5,
pListLast: 0xff3,
...
}
0xff5: {
h: 3,
pListNext: NULL, // он был добавлен последним
pListLast: 0xff4,
...
}
What happens after the array overflows is called rehash. Essentially, iterating over all existing buckets (via pListNext), assigning their neighbors (collisions), and adding references to them in arBuckets.
But what actually happens when an element is received by key? Something else will be added to the previous algorithm:
- If the key is string, then the string is hashed to integer-a (the DJBX33A hash algorithm is used):
- The original value of the hash is taken as magic 5381
- For each key symbol, multiply the hash by 33 and add the character number in ASCII
- A mask (bitwise and) is always applied to the resulting numeric key, which is always equal to the size of the array (which is with buckets) minus 1
- We take out a bucket on an index
- If the key of this bucket is equal to the desired one, the search is completed, otherwise:
- In the loop we take a bucket from pNext (if it exists) and see if the key is equal
So until either the buckets in pNext run out (then Notice will be thrown), or until a match is found.
It is worth noting that in PHP almost everything is built on this HashTable structure alone: all variables lying in any scope actually lie in HT, all class methods, all class fields, even class definitions themselves, lie in HT, it is actually a very flexible structure. Among other things, HT provides almost the same speed of fetching / inserting / deleting and the complexity of all three is O (1), but with the caveat for a small overhead in case of collisions.
By the way, here I implemented a Hash Table in PHP itself. Well, that is, implemented PHP arrays in PHP =)
