One of the methods of protest is the filing and collective signing of various kinds of petitions. But since the list of signatories to the petition is open, there are often situations when those who disagree with the “party’s course” are threatened and repressed by the administration.

Is it possible to create a system that allows anonymous collection of signatures, but at the same time gives the opportunity to verify each vote? I bring to your attention my solution to this problem.

Formulation of the problem

There is a limited circle of people, for example, students of an institute, employees of an organization, or citizens of a country. Some of them sign a message (petition, collective appeal, etc.). The proposed signing algorithm has the following properties:

1. It is possible to make sure that each signatory belongs to the specified circle of persons.
2. It is possible to verify that most signatures belong to different persons.
3. There is no way to determine to whom exactly this or that signature belongs.
4. It is not possible to determine whether a particular person has left his signature or not.
5. Any signatory can, at his request, put a personalized one instead of an anonymous signature.
6. Any anonymous signer may subsequently, at his request, provide evidence that he has signed.

The system is based on asymmetric cryptography , digital signature algorithms and key certification .

Preparatory stage

Each participant (Fig. 1 - A, B, ... Z ) generates a key pair, public and private. We will call these keys personalized . The public key is published and confirmed by a certification center, which may be the dean's office of the institute, the personnel department of the enterprise or the administrative apparatus of the state. The purpose of the certificate is to confirm that this key really belongs to the specified person, and that this person has the right to participate in collective signing.


Fig. 1. Public key certification scheme

This stage is carried out once, regardless of the number of messages signed in the future. The certified key database can be stored centrally or distributed.

Vote formation

Each signer generates another key pair - the so-called anonymous keys . Using the private key, he signs the message, and the public publishes anonymously. Electronic signature (EDS) and the corresponding public key are one vote .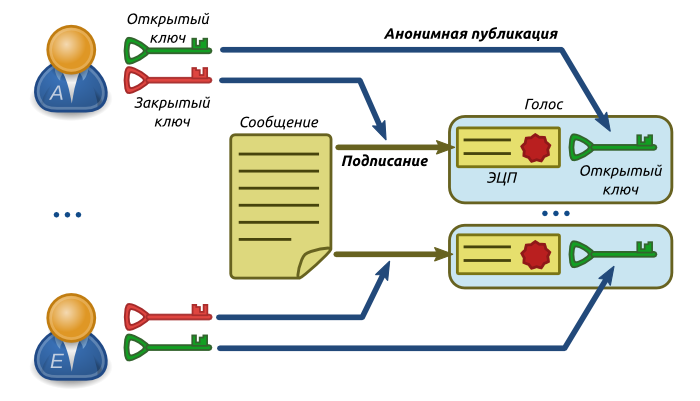


Fig. 2. Voting scheme

If the signatory wants to refuse anonymity, he can use his personalized key for signing and not generate anonymous keys at all.

Voice check

The initial verification of votes consists in the fact that the observer (in the role of which anyone can play) checks the signature of each vote using the corresponding public anonymous key. Thus, the observer makes sure that this voice is formed specifically for this particular message. But so far nothing can be said either about the uniqueness of the signatories, nor about their belonging to the indicated circle of persons.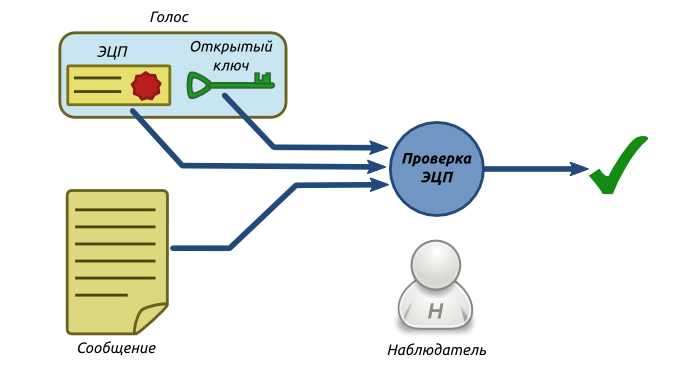


Fig. 3. The scheme of the initial voice check

Signature Verification

Subsequently, verification of signatories is carried out. This check can be either selective or complete, depending on the number of signatories and technical capabilities.

The observer publishes a request to verify a specific voice using an anonymous public key as an identifier. The signatory whose key is published in the request (Fig. 4 - A ) generates a random control message and publishes it anonymously. In principle, the observer can also generate this message by attaching it to the request.

Then A signs the control message with his anonymous private key. Next, A selects a certain group of persons, including himself (in Fig. 4 - A, B, C) It does not matter whether the signer is someone from the group other than A , and besides, it is impossible to establish. And it breaks the digital signature of the control message into fragments, in accordance with the number of group members and distributes these fragments among them.

The division into fragments in the figure is shown conditionally. Simply cutting text, even with rearranging characters, is a bad decision. It is better to use one of the secret sharing algorithms .

Each member of the group (including A himself ) signs his fragment with his personalized private key and then publishes it.


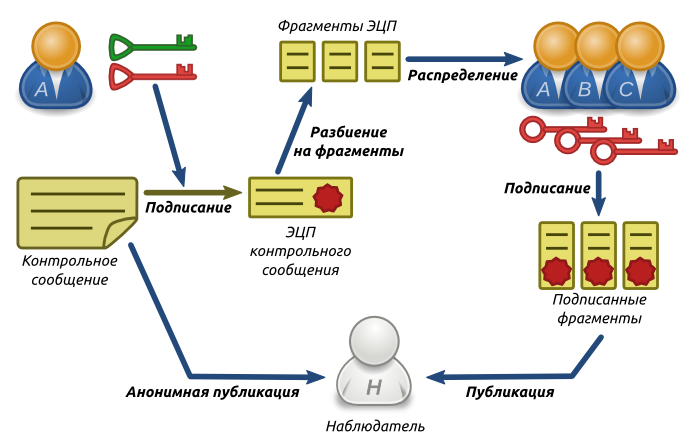
Fig. 4. Signature verification scheme

Thus, the observer receives evidence that the voice was formed by someone from the group {A, B, C} , but it is impossible to say who exactly. This makes it very difficult for the administration to apply reprisals to signatories. The group size can be chosen arbitrarily, the higher it is, the higher the reliability, but the more difficult (technically) to organize the distribution of fragments. It is necessary to prohibit repeated verification of the voice, otherwise it becomes possible to calculate the signatory by looking for intersections of the groups involved in each verification. Or to demand that the composition of the group does not change upon repeated verification.

If the signatory wants to deanonymize, he performs all the same actions, only does not collect the group, but simply signs the control message with his private keys: anonymous and personalized.

Fragmentation and signing

Let us dwell in more detail on the fragment distribution algorithm. The following requirements are imposed on him:

1. None of the group members and outside observers should be able to find out who initiated the procedure.
2. Even if all members of the group, except A , are conspiring, they should not have the opportunity to prove that it is A who is the initiator.
3. A person who is not part of the group should not be able to initiate the procedure.

The latter requirement renders unsuitable simple anonymous distribution of fragments. After all, then it becomes possible for the person to “generate a voice” and undergo verification by sending fragments to the others and not signing with their personalized key.

The fragment distribution diagram is shown in Fig. 6. Suppose A is the initiator. He signs with his private key Personalize occasional snippet, and then sends all the fragments Bed and . First of all, B verifies the signature of A using a certified public key, and making sure that A is the one he claims to be, publishes the signed fragment.

Then B removes the signature from the messageAnd , signed with his private key Personalize following snippet and sends all the fragments C . Similarly, C verifies the signature of B , publishes this fragment, and signs the next.

At the end of the chain, the message is again forwarded to A , which checks the signature of the last participant ( C ) and publishes the last fragment.


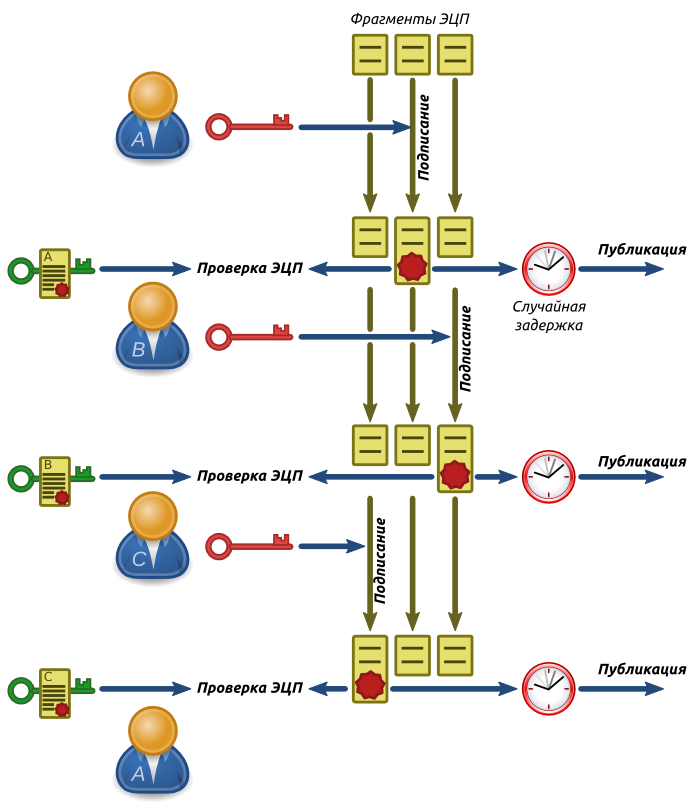
Fig. 5. Scheme of distribution and signing of fragments

For each participant, except the initiator, the procedure looks exactly the same and there is no way to determine where the beginning of the chain and where its end. Even if B and C conspire and determine the sequence of transfers, Awill be able to claim that he is in the chain after C (respectively, B is the initiator), and B with C will have no way to prove the opposite.

To prevent timing attacks, the publication of signed fragments must be done after the completion of the procedure, or introduce random delays before publication. Also, all members of the group must pre-cache the public keys and certificates so that the order could not be established by the time of access to the certification server.

Verification Completion

The observer received signed fragments verifies each signature of the public keys A , B and C . Then he collects from the fragments the signature of the control message and verifies it using the original control message and the anonymous public key from the verified voice. If the verification of all EDS was successful, the verification is considered passed.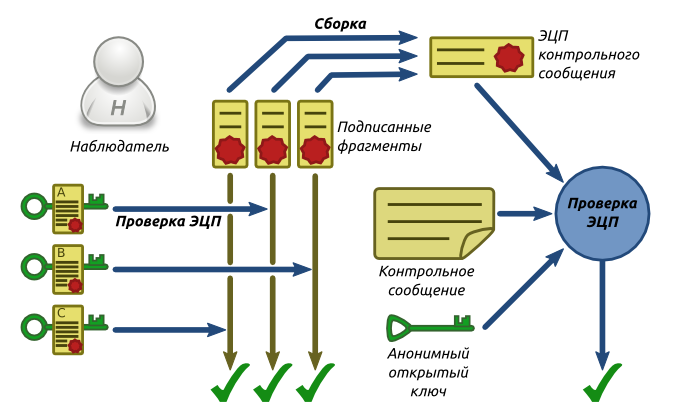


Fig. 6. Scheme of the final verification stage

All operations performed by the observer can be repeated by any other party, since the initial data (voice, control message and signed fragments) are published in the public domain.

Conclusion

Despite the fact that a two-day search for existing analogues of the proposed algorithm did not yield results, I would not be surprised at all if it turns out that I invented another bike. If this is true, I will be grateful for the links. After all, cycling is a great exercise for the brain. I will also be very grateful to the community for the search for inaccuracies, vulnerabilities, and places where the algorithm can be improved.

Thank you for attention!

UPD

I really invented a bike. To solve this problem, the class of algorithms Group / Ring signatures is intended . Thanks grich for the tip!