What happened to the Fermi paradox

The Fermi paradox lies in the fact that the probability of an extraterrestrial civilization is usually estimated quite high, and there is nothing to see signs of its existence. Recently, a preprint by Sanders and co-authors “Dissolving the Fermi paradox” appeared on arxiv , which has already been interpreted as the abolition of this paradox (true), idle chatter in the absence of data (most likely, but true for the Fermi paradox in general, and not just for this article) , and as evidence of the non-existence of aliens and / or low L (false). In this article we will try to figure out what the preprint actually contains.

What's the matter?

First of all, the Drake equation itself. It is presented on the KDPV; the last multiplier is a joke, and the rest should be understood as follows: in the observable universe (or our galaxy, or any other space) there is$$stars Every star with probability$$has a planet. Each of these planets with probability$$is in the Goldilocks area, has a livable chemical composition, etc. On every potentially life-sustaining planet, with probability$$ (per unit of time) life arises, which with probability $$ achieves rationality and probability $$gets in touch. And finally, every rational species that emerges exists$$years from birth to extinction. If you multiply it all, you get a number of reasonable species in a given area.

The time between the origin of the mind and the appearance of a civilization noticeable in the interstellar distances is neglected. In the case of the Earth, for example, billions of years have passed from the appearance of the planet to the appearance of life and from the appearance of life to the appearance of the species Homo sapiens . Technological progress is incomparably faster - the emergence of Homo sapiens is less than ten million years from the message of Arecibo. Interstellar colonization has not yet begun, but this is also, in the worst case, a matter of a couple of million years. Compared with pre-technological stages - within the limits of error.

Which, how to say it more practical, is quite high. From the order of magnitude for the number of stars and the probability that they have planets up to 200 orders of magnitude (two hundred orders of magnitude, the estimates differ in$$times) for the probability of abiogenesis. The ungrateful thing is to evaluate the probabilities from a single observation. However, scientists published various estimates$$ and most often came to the conclusion that $$or even $$. What, in fact, is the Fermi paradox: according to our best estimates, there should be other reasonable races in the galaxy, and there is no reliable evidence of their existence.

The problem is obviously not in the galaxy: if the estimates differ from the observed reality, then so much the worse for the estimates. Either one of the parameters is greatly overestimated ( and God bless us if it is L ), or we somehow incorrectly believe. Sandberg et al. Protect the latest version.

And how to count correctly?

It would seem to multiply a handful of real numbers - not Bin Newton. The catch is that in such a situation, the multiplication of numbers relies on the assumption that they are somehow known to us. As we saw above, this assumption is very far from reality.

Consider a simplified example: let the Drake equation have nine parameters and all nine are uniformly distributed in the range$$. The best point estimate for each such parameter is 0.1 and their product gives a probability of one civilization per billion stars. In the galaxy from$$ There should be about 100 civilizations of stars, and the likelihood that this will not happen even once - $$. Such probabilities are usually illustrated with phrases like “if every atom in <some very big thing like the solar system> for <some very long time like its age>”. That in this case sounds quite appropriate, but in fact it is impossible not to reject such a null hypothesis. The Fermi paradox rises to its full height.

If we do not use point estimates, and for each parameter we take a random variable from the corresponding range, then the galaxy is empty in 21.45% of simulations. The fact that something happened to the probability of a little more than one-fifth is not a paradox. This is slightly less likely that a pair of kings will beat all the other hands on the 9-player hold'em table , and I personally go all-in with pocket kings at the first opportunity.

The same logic can be applied to real estimates of the parameters of the Drake equation. If we collect them from literature and drive away the simulations, we get the following picture:



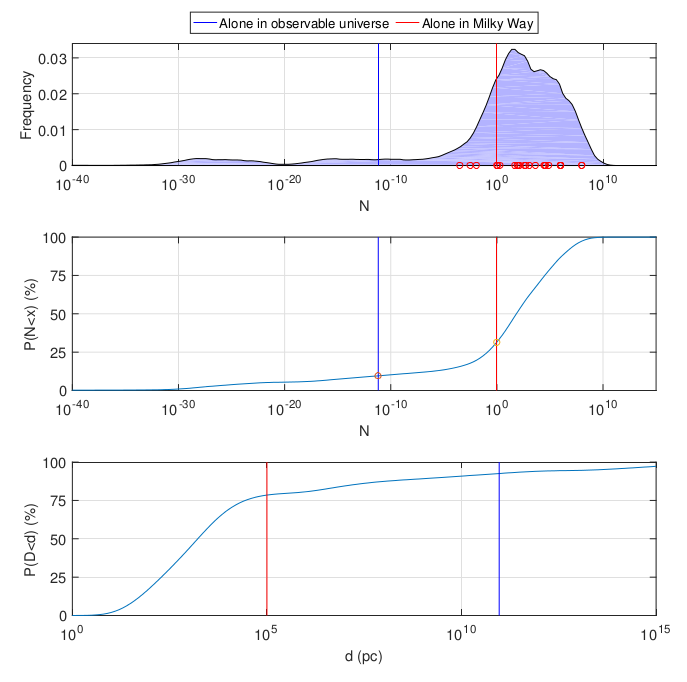
Top down: probability density function for the number of civilizations in our galaxy, cumulative distribution density for it, cumulative distribution density of the distance to the nearest observable civilization in parsecs. All - on a logarithmic scale. The red and blue lines indicate the probability that we are the only civilization in our galaxy and the observable universe. Circles on the top chart - normalized literary ratings$$.

In general, the result is rather optimistic: the greatest probability density falls on the multiplicity of civilizations (average 53 million, median 100). But for the purposes of the Fermi paradox, the figures are roughly the same as in the simplified example: with a probability of twenty percent of something, the Milky Way contains only one civilization (ours). By the way, a rather counterintuitive consequence: the probability that the Milky Way, not counting the Earth , contains exactly one civilization (except ours), is almost the same.

Instead of taking parameter estimates from the literature directly, one can construct distributions and calculate them analytically. A range of estimates is taken up to the order of magnitude and each parameter is considered log-normal or log-uniformly distributed in the corresponding interval. The result shifts somewhat to the left, but the meaning is the same:



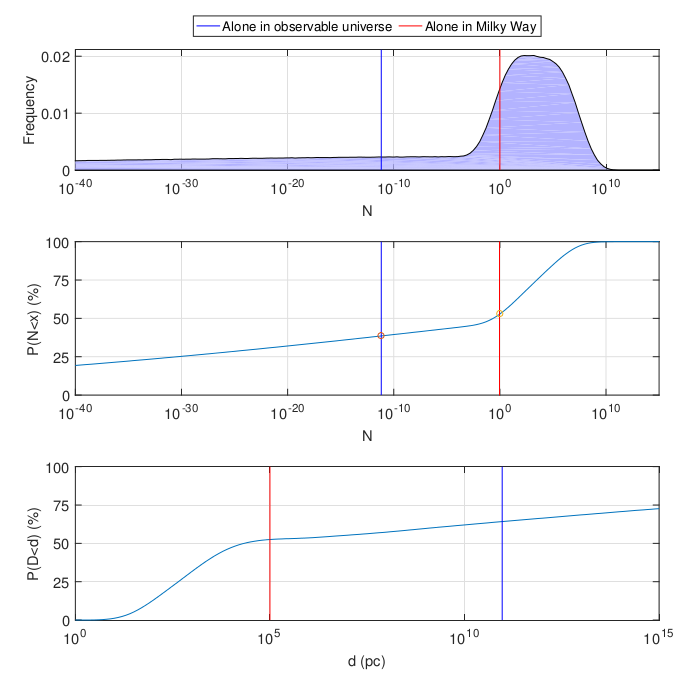
What does all this mean? The correct answer to the question “is there life in the universe or is it not there” is still “I don't know”. Arguably graceful Bayesian statistics are worth little in the absence of experimental data. The answer to the question “how much we should be surprised by the observed$$". He used to be “Very strong, so either life is a very rare thing, or we will all die in a nuclear war or something like that, ” and now it’s become “Well, in principle, not very likely, but nothing extraordinary.” The probability of nuclear war and / or meeting with a dinosaur on Nevsky by aliens fell only in the Bayesian sense: we are a little less sure that this will happen. Whether these events actually occur or not depends on the factors of the real world (roughly speaking, Putin, Trump and Zorblax, Galactic Eater), and not the mathematics used to discuss them.