Handling 2D Collisions Using LibCanvas
In most modern games, it is impossible to do without the detection and further processing of collisions (shot, jump, banal rebound from an obstacle). At first glance, their implementation seems quite simple, but is it really so? I’ll try to briefly explain the essence of the problems that I encountered.
By tradition, after reading several articles, you begin to feel like a god who can do anything. I think many have encountered a similar problem and can imagine what will follow it ... correctly, a series of big problems. But first things first.
Preparation of the “landscape”
So where to start? It seems to me that it is best to start with static objects, because it is much easier to work with them (no need to worry about redrawing, changing position / shape and other things).
var background = new LibCanvas('#canv') .size(512, 512).start(); //создаем объект LibCanvas
background.createShaper({ //и строим на нем некоторое препятствие
shape : shape,
stroke: '#00f',
fill : '#004'
});Creating an object concept
Next, you can consider, in fact, the “object” (that which moves around the canvas and will bounce off obstacles) . I believe that consideration of the object should begin from the end, namely, from what it will have to be able to do in the end.
Each one will have his own list, but for me it looks like this:
- the object must know its position and size
- the object must know the direction and speed of its movement
- the object must know what it looks like
- the object must be able to print onto the canvas, as well as “reprint” (delete from one place and appear in another)
- the object must be able to detect collisions with the borders of the canvas
- the object must be able to detect and handle collisions with obstacles
Object implementation
To begin with, we need to create a separate layer for moving objects (so as not to redraw other layers each time, for example, background) :
var cont = background.createLayer('cont');Now on this layer you need to place the object, which will be set as follows:
var object = {
center: {x, y}, // центр объекта
speed: {x, y}, // скорость
size, // его размер
buffer, // изображение на холсте
redrawBuffer(), // функция, для изменения object.buffer
print(), // перенос изображения из буффера на холст
redraw(), // перенос изображения из одного места холста на другое
animate(), // определение столкновений с границами холста
findBounce() // определение и обработка столкновений с препятствиями
};The following question arises: how to fill in the attributes of this object? Let's go in order.
Center, speed and size
Let us catch 2 clicks on the canvas - the coordinates of the first is the center of the object, and using the coordinates of the second it will be easy to calculate the components 'x' and 'y' of the speed of the object.
No sooner said than done. We realize:
cont.listenMouse(); // начинаем “слушать” мышь
var mouse = cont.mouse;
var flag = false; // необходим для определения клика – первый или второй
mouse.addEvent('mousedown', function() {
flag = !flag;
});
cont.addRender(function() {
if(mouse.inCanvas) {
if(flag) {
object.size = size; //устанавливаем необходимый размер объекта
object.center.center.moveTo( mouse.point );
object.speed.x = 0; // а также не забываем обнулить скорость
object.speed.y = 0;
}
else { // если второй клик
object.speed.x = mouse.point.x – object.center.x; // при втором клике устанавливаем скорость объекта
object.speed.y = mouse.point.y - object.center.y;
}
}
});So, let's go further.
What is object.buffer, object.redrawBuffer, object.redraw and why are they actually needed
A bit of theory - when you call the cont.update () function , a request is sent to redraw to the next rendering stage (if you synchronously call “update” five times in a row, then the redraw will be done only once - when the next frame is rendered) . But, one way or another, the entire canvas will be redrawn, which is rather inefficient (a little math: canvas (512 * 512) = 262144 points, the size of the object - even if 50 * 50 = 2500 points, which is about 10 times smaller than the whole canvas ) .
Since we will move our object, which means we will redraw the canvas many times, it will be much more efficient to simply cut the image from one place and paste it into another. This is the easiest way, for those who do not want to think, but want to solve problems directly “in the forehead”. The following option is much more interesting, at least for me: we don’t cut the image of the object from the canvas and save it to the buffer each time we move, but we have two functions - redrawBuffer () and redraw (fromX, fromY, toX, toY) . In case of changing the appearance of the object, the first one is suitable: redrawBuffer (), which changes the contents of the buffer. To move, you can use the redraw function (fromX, fromY, toX, toY), which “cleans” the place under the object in the “old” place and inserts the image from the buffer into the “new” one:
redraw: function(canvas, beforeX, beforeY, afterX, afterY) {
var params = {
fromX: (beforeX - this.size),
fromY: (beforeY - this.size),
size: (this.size*2),
toX: (afterX - this.size),
toY: (afterY - this.size)
}
canvas.ctx.clearRect(params.fromX - 1, params.fromY - 1, params.size + 2, params.size + 2);
canvas.ctx.drawImage(this.buffer, params.toX, params.toY);
}Object reaction to collisions with canvas borders
It is realized to horror simply - if the object has reached the upper or lower edge, then:
object.speed.y = -object.speed.y;if right or left:
object.speed.x = -object.speed.x;Detection and handling of collisions with obstacles
How to understand where the object should bounce after colliding with an obstacle of arbitrary shape? The answer to this question can be given to us by old school books with a course in physics / geometry - “the angle of incidence is equal to the angle of reflection”. Since not everyone can remember physics and geometry, I think it’s worth recalling that these angles are counted from the normal (perpendicular) to the surface at a point:
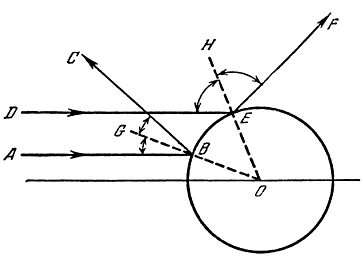
Here 'H' and 'G' are normals. 'A' and 'D' - speeds before a collision. 'C' and 'F' are speeds after a collision.
But, as often happens, in words everything is quite simple, but in reality, alas, no.
So, I'll start with a fairly general algorithm:
- We move the object until it encounters an obstacle.
- We find the normal
- Change speed
- We return to paragraph 1
We move the object until it encounters an obstacle.
With moving everything is simple: draw an object, change the position of its center, erase the old one, draw a new one - that’s all movement. But how to understand that two objects (object and background) collided? To do this, I want to recall that now the canvas has two layers (“background” - static and “object” - dynamic) , and we need to understand that 2 objects intersected (or just touched). After reading this article, I more or less imagined an algorithm for finding the intersection:
- we get an image of a layer with an object and an image of a layer with an obstacle
- recall that: “ Pixels are stored in objects of type ImageData. Each object has three properties: width, height and data. The data property is of type CanvasPixelArray and contains an array of elements of size width * height * 4 bytes; that means each pixel contains RGBA color. ”
- write a simple loop in which there is only one condition
var pixels1 = background.ctx.getImageData( x,y,size,size);
var pixels2 = cont.ctx.getImageData( x,y,size,size);
for(var i = 0; i < pixels2.length; i += 4 ) {
if((pixels1[i+3] != 0) && (pixels2[i+3] != 0)) {
/* имеем столкновение */
break;
}
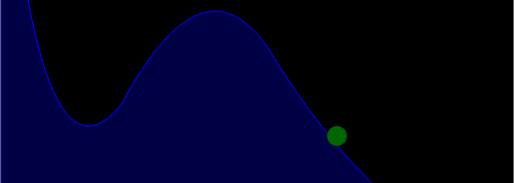
}At this stage, I would again advise you to ask about efficiency - is it worth it to run 2 * 512 * 512 pixels with each movement of the object? Of course not. It is possible without any consequences to reduce the “search zone” to the square into which the object can be accommodated (of course, if there is only one moving object) . But is it possible to reduce this area even more, say, to 1 pixel? Yes you can. But this further “decrease” will affect the accuracy of the collision. As an example, I’ll give a picture where the green circle is the object and the blue bar is the obstacle:

If we were to take the “search zone” equal to (object.size * 2) * (object.size * 2) (object.size - radius), then the collision would be established, but if only 1 pixel (center) was selected for the calculation, then the collision is not defined.
How to act for you is a purely personal matter, but I decided to sacrifice accuracy and began to work with the center of the object.
Collision is established, but what's next? What to do with the scary word “normal”?
We find the normal
There are two ways - the right one and mine.
Method 1. Correct:
- find the touch zone
- we find the boundary points of the obstacle from this zone
- interpolate them and find the normal equation at the point of tangency

Method 2. Incorrect:
- we get the zone of intersection of the object and the obstacle.
- we find the center of this zone:
var avgPoint{x:0, y:0, number:0};
for(var i = 0; i < pixels2.length; i += 4 ) {
if((pixels1[i+3] != 0) && (pixels2[i+3] != 0)) {
avgPoint.x += (i/4)%(this.size*2);
avgPoint.x += Math.round((i/4)/(this.size*2));
}
}
avgPoint.x = Math.round((avgPoint.x / avgPoint.number) + this.center.x - this.size);
avgPoint.y = Math.round((avgPoint.y / avgPoint.number) + this.center.y - this.size); - we connect the found center of the “intersection zone” (avgPoint.x, avgPoint.y) with the center of the object. This will be normal.

Change speed
So, we open the textbooks again and find out that when reflected, the normal component of the velocity changes sign, while the tangential (normal to the perpendicular) remains unchanged.
So we have the task of expanding the velocities from the (x, y) coordinate system into the (n, t) coordinate system. Here the usual geometry from high school comes to the rescue:
var hyp = Math.hypotenuse((avgPoint.y - object.center.y),(avgPoint.x - object.center.x))
var sinNA = (avgPoint.y – object.center.y)/hyp;
var cosNA = (object.center.x - avgPoint.x)/hyp;
var nSpeed = this.speed.x * cosNA - this.speed.y * sinNA;
var tSpeed = this.speed.x * sinNA + this.speed.y * cosNA;
nSpeed = -nSpeed;
object.speed.x = (tSpeed * sinNA + nSpeed * cosNA);
object.speed.y = (tSpeed * cosNA - nSpeed * sinNA);That's all, our object can change the direction of speed depending on the shape of the obstacle encountered. It remains to combine all the functions and objects in the final script and see the
result .
On this my article is over, thanks for your attention!
