Mysterious Number 6174
- Transfer
The number 6174 is truly mysterious. At first glance, it may seem that there is nothing unique in it. But as we will see later, everyone who knows how to count can discover the secret that makes the number 6174 so special.
This is a simple action, but Kaprekar found that it leads to an amazing result. Let's see how it works, for example, on the number 2005. From these numbers we can get the maximum number 5200, and the minimum number 0025, that is 25. Subtractions will look like this:
5200 - 0025 = 5175
7551 - 1557 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
When we reach 6174, the function repeats itself, returning 6174 each time. We call the number 6174 a fixed point for this function. This number makes the series of subtractions stop, but is it really just this that makes it special? Another surprise awaits us here. Let's try to repeat the operation on some other number, for example, 1789.
9871 - 1789 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
We got 6174 again!

When we started in 2005, we reached 6174 in seven steps, and for 1789 the process took three steps. In fact, you get 6174 for any four-digit number in which all digits are not the same. This is amazing, isn't it? Kaprekar's function is so simple, but gives such an interesting result. And it gets even more interesting when we think about the reasons why all four-digit numbers reach the mysterious number 6174.
9 ≥ a ≥ b ≥ c ≥ d ≥ 0
where a, b, c, d are not the same digits, the maximum number is abcd , and the minimum is dcba .
We can calculate the result of the Kaprekar function by composing a system of equations.
abcd-
dcba
____
ABCD
which gives the following result
D = 10 + d - a (if a> d)
C = 10 + c - 1 - b = 9 + c - b (if b> c - 1)
B = b - 1 - c (if b> c)
A = a - d
for numbers, where a> b> c> d .
The result will begin to repeat if the final number ABCD can be written with the original four digits a, b, c and d . So we can find the fixed point of the Kaprekar function by going through all possible combinations {a, b, c, d} and checking whether the above conditions are satisfied. Each of 4! = 24 combinations gives a system of four equations with four unknowns, so that we should not have problems with solving this system for a, b, c and d .
It turns out that only one of these combinations has an integer solution that satisfies the requirement9 ≥ a ≥ b ≥ c ≥ d ≥ 0 . This is a combination of ABCD = bdac , and the only solution to the system of equations is a = 7, b = 6, c = 4, and d = 1 . That is, ABCD = 6174. For identical digits {a, b, c, d} , the system does not have a valid solution. Therefore, the number 6174 is the only fixed point of the Kaprekar function - our mysterious number is unique.
For three-digit numbers, the same phenomenon is observed. For example, applying the Kaprekar function to the number 753 gives the following:
753 - 357 = 396
963 - 369 = 594
954 - 459 = 495
954 - 459 = 495
The number 495 is a unique fixed point for three-digit numbers, and all three-digit numbers ultimately come down to it. You can check it yourself.
The table below shows the result: each number reaches 6174 in a maximum of seven iterations. If you have not reached 6174 in seven iterations, then you just have a calculation error and you need to try again!
My computer program checked all 8,991 numbers, but Malcolm Lines in his article [Lines, Malcolm E., A number for your thoughts: facts and speculations about numbers ..., Bristol: Hilger (1986)] proves that just 30 possible four-digit numbers to check the Kaprekar function.
As before, let's represent the four digits as abcd , where
9 ≥ a ≥ b ≥ c ≥ d ≥ 0 .
Let's calculate the first action in the chain. The maximum number is 1000a + 100b + 10c + d , and the minimum is 1000d + 100c + 10b + a . So the subtraction operation will be reduced to the following:
1000a + 100b + 10c + d - (1000d + 100c + 10b + a)
= 1000 (ad) + 100 (bc) + 10 (cb) + (da)
= 999 (ad) + 90 (bc)
A positive value (ad) is in the range from 1 to 9, and (bc) is in the range from 0 to 9. Going through all the possible options, we can see all the possible results of the first subtraction action. They are shown in the table.

We are only interested in numbers in which the digits are not the same and
a ≥ b ≥ c ≥ d ,
therefore we take only those in which (ad) ≥ (bc) . So we can ignore the entire gray area in the table containing numbers in which
(ad) <(bc) .
Now we will rearrange the numbers in the table in descending order to get the finished minimum number for the second subtraction.
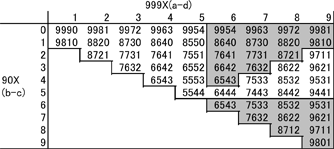
We can ignore duplicates (gray area) and there are exactly 30 numbers left to continue the operation. The following diagram shows the routes in which all these numbers come to the same result 6174.
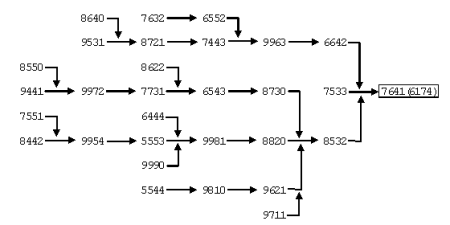
From this diagram you can see how all four-digit numbers reach 6174 and this happens in a maximum of seven iterations. But even after that, it seems to me that the number 6174 remains rather mysterious. I believe that Kaprekar, who discovered this number, was extremely smart and had a lot of time to think about this problem!
82 - 28 = 54
54 - 45 = 9
90 - 09 = 81
81 - 18 = 63
63 - 36 = 27
72 - 27 = 45
54 - 45 = 9
After a short time, we will see that all two-digit numbers form a cycle 9 → 81 → 63 → 27 → 45 → 9. Unlike three- and four-digit numbers, there is no unique fixed point.
And what about five-digit numbers? Is there a unique fixed point for them, such as 6174 and 495? To answer this question, we have to do a similar operation: check all 120 combinations{a, b, c, d, e} for ABCDE , so that the following conditions are met:
9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0
and
abcde - edcba = ABCDE .
Fortunately, all the necessary calculations have already been done on the computer and it is known that for the Kaprekar function on five-digit numbers there is no unique constant point. But all five-digit numbers come down to one of three cycles:
71973 → 83952 → 74943 → 62964 → 71973
75933 → 63954 → 61974 → 82962 → 75933
59994 → 53955 → 59994
As Malcolm Lines notes in his article, it takes a long time to check numbers with six and a large number of digits, and this work becomes extremely tedious. To save you from such a fate, the following table contains the constant points of all numbers from two to ten digits (for the rest - see Mathews Archive of Recreational Mathematics ).
Let's stop and think about a beautiful puzzle composed by Japanese author Yukio Yamamoto.
If you multiply two five-digit numbers, you can get the result 123456789. Guess these two numbers.
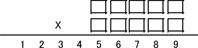
This is a very beautiful puzzle, and you can assume that some great mathematical theory is hidden behind it. But in fact, her beauty is extremely random, there are other similar, but not so beautiful examples:
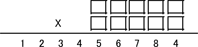
(We can give you a hint for solving these problems, and here are the answers .)
If I show you the Yamamoto puzzle, then it will be interesting for you to solve it, because it is beautiful, but if I show you the second puzzle, then it may not interest you at all . I think Kaprekar’s problem is similar to Yamamoto’s number search problem. We like these puzzles because they are beautiful. And for the same reason, it seems to us that there should be more to them than a mere coincidence. Such misunderstandings have repeatedly led to scientific discoveries in mathematics and the science of the past.
Is it enough to know that all four-digit numbers are reduced to the number 6174 as a result of the Kaprekar function, but not to know why? Until now, no one could say with certainty that a unique fixed point for three- and four-digit numbers is just a random phenomenon. It seems such an amazing property that we can expect it to have some kind of big theorem from number theory. If we could answer this question, perhaps in the end it would turn out that we are just faced with a beautiful misunderstanding, but we hope that this is not so.
Caprecar Function
In 1949, the mathematician D.R. Kaprekar from the city of Dolali (India) invented the mathematical action, which is now known as the Kaprekar function. First, select any number in which the digits do not repeat (that is, not 1111, 2222, etc.). Then rearrange the numbers to get the largest number possible and the smallest possible. Then you need to subtract the smaller from the larger - and repeat the operation with the resulting number.This is a simple action, but Kaprekar found that it leads to an amazing result. Let's see how it works, for example, on the number 2005. From these numbers we can get the maximum number 5200, and the minimum number 0025, that is 25. Subtractions will look like this:
5200 - 0025 = 5175
7551 - 1557 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
When we reach 6174, the function repeats itself, returning 6174 each time. We call the number 6174 a fixed point for this function. This number makes the series of subtractions stop, but is it really just this that makes it special? Another surprise awaits us here. Let's try to repeat the operation on some other number, for example, 1789.
9871 - 1789 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
We got 6174 again!

When we started in 2005, we reached 6174 in seven steps, and for 1789 the process took three steps. In fact, you get 6174 for any four-digit number in which all digits are not the same. This is amazing, isn't it? Kaprekar's function is so simple, but gives such an interesting result. And it gets even more interesting when we think about the reasons why all four-digit numbers reach the mysterious number 6174.
Only 6174?
From the digits of each four-digit number, you can get the maximum number if you rearrange the numbers in descending order, and the minimum number is obtained by rearranging them in ascending order. For four digits a, b, c, d :9 ≥ a ≥ b ≥ c ≥ d ≥ 0
where a, b, c, d are not the same digits, the maximum number is abcd , and the minimum is dcba .
We can calculate the result of the Kaprekar function by composing a system of equations.
abcd-
dcba
____
ABCD
which gives the following result
D = 10 + d - a (if a> d)
C = 10 + c - 1 - b = 9 + c - b (if b> c - 1)
B = b - 1 - c (if b> c)
A = a - d
for numbers, where a> b> c> d .
The result will begin to repeat if the final number ABCD can be written with the original four digits a, b, c and d . So we can find the fixed point of the Kaprekar function by going through all possible combinations {a, b, c, d} and checking whether the above conditions are satisfied. Each of 4! = 24 combinations gives a system of four equations with four unknowns, so that we should not have problems with solving this system for a, b, c and d .
It turns out that only one of these combinations has an integer solution that satisfies the requirement9 ≥ a ≥ b ≥ c ≥ d ≥ 0 . This is a combination of ABCD = bdac , and the only solution to the system of equations is a = 7, b = 6, c = 4, and d = 1 . That is, ABCD = 6174. For identical digits {a, b, c, d} , the system does not have a valid solution. Therefore, the number 6174 is the only fixed point of the Kaprekar function - our mysterious number is unique.
For three-digit numbers, the same phenomenon is observed. For example, applying the Kaprekar function to the number 753 gives the following:
753 - 357 = 396
963 - 369 = 594
954 - 459 = 495
954 - 459 = 495
The number 495 is a unique fixed point for three-digit numbers, and all three-digit numbers ultimately come down to it. You can check it yourself.
How fast is 6174?
It was around 1975, when I first heard about the number 6174 from a friend, and then I was very impressed. I thought it would be quite simple to explain the reasons for this phenomenon, but I could not find an explanation. I checked on the computer all four-digit numbers. The program took about 50 lines in Visual Basic and it checked all 8991 four-digit combinations from 1000 to 9999, where the characters are not repeated.The table below shows the result: each number reaches 6174 in a maximum of seven iterations. If you have not reached 6174 in seven iterations, then you just have a calculation error and you need to try again!
| Iterations | Amount of numbers |
| 0 | one |
| one | 356 |
| 2 | 519 |
| 3 | 2124 |
| four | 1124 |
| five | 1379 |
| 6 | 1508 |
| 7 | 1980 |
As before, let's represent the four digits as abcd , where
9 ≥ a ≥ b ≥ c ≥ d ≥ 0 .
Let's calculate the first action in the chain. The maximum number is 1000a + 100b + 10c + d , and the minimum is 1000d + 100c + 10b + a . So the subtraction operation will be reduced to the following:
1000a + 100b + 10c + d - (1000d + 100c + 10b + a)
= 1000 (ad) + 100 (bc) + 10 (cb) + (da)
= 999 (ad) + 90 (bc)
A positive value (ad) is in the range from 1 to 9, and (bc) is in the range from 0 to 9. Going through all the possible options, we can see all the possible results of the first subtraction action. They are shown in the table.

We are only interested in numbers in which the digits are not the same and
a ≥ b ≥ c ≥ d ,
therefore we take only those in which (ad) ≥ (bc) . So we can ignore the entire gray area in the table containing numbers in which
(ad) <(bc) .
Now we will rearrange the numbers in the table in descending order to get the finished minimum number for the second subtraction.

We can ignore duplicates (gray area) and there are exactly 30 numbers left to continue the operation. The following diagram shows the routes in which all these numbers come to the same result 6174.

From this diagram you can see how all four-digit numbers reach 6174 and this happens in a maximum of seven iterations. But even after that, it seems to me that the number 6174 remains rather mysterious. I believe that Kaprekar, who discovered this number, was extremely smart and had a lot of time to think about this problem!
Two digits, five digits, six or more ...
We have already seen that four- and three-digit numbers reach a unique fixed point, but what about numbers with a different number of characters? It turns out that for them the result is not so impressive. Let's try a two-digit number, for example, 28:82 - 28 = 54
54 - 45 = 9
90 - 09 = 81
81 - 18 = 63
63 - 36 = 27
72 - 27 = 45
54 - 45 = 9
After a short time, we will see that all two-digit numbers form a cycle 9 → 81 → 63 → 27 → 45 → 9. Unlike three- and four-digit numbers, there is no unique fixed point.
And what about five-digit numbers? Is there a unique fixed point for them, such as 6174 and 495? To answer this question, we have to do a similar operation: check all 120 combinations{a, b, c, d, e} for ABCDE , so that the following conditions are met:
9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0
and
abcde - edcba = ABCDE .
Fortunately, all the necessary calculations have already been done on the computer and it is known that for the Kaprekar function on five-digit numbers there is no unique constant point. But all five-digit numbers come down to one of three cycles:
71973 → 83952 → 74943 → 62964 → 71973
75933 → 63954 → 61974 → 82962 → 75933
59994 → 53955 → 59994
As Malcolm Lines notes in his article, it takes a long time to check numbers with six and a large number of digits, and this work becomes extremely tedious. To save you from such a fate, the following table contains the constant points of all numbers from two to ten digits (for the rest - see Mathews Archive of Recreational Mathematics ).
| Discharges | Constant point |
| 2 | Not |
| 3 | 495 |
| four | 6174 |
| five | Not |
| 6 | 549945, 631764 |
| 7 | Not |
| eight | 63317664, 97508421 |
| 9 | 554999445, 864197532 |
| ten | 6333176664, 9753086421, 9975084201 |
Fine, but what is the reason?
We made sure that all three-digit numbers are reduced to 495, and all four-digit numbers are reduced to 6174 as a result of calculating the Kaprekar function. But I did not explain why all these numbers have a unique fixed point. Is this phenomenon random or does it have a deeper mathematical explanation? It is wonderful and mysterious that this could be a mere coincidence.Let's stop and think about a beautiful puzzle composed by Japanese author Yukio Yamamoto.
If you multiply two five-digit numbers, you can get the result 123456789. Guess these two numbers.

This is a very beautiful puzzle, and you can assume that some great mathematical theory is hidden behind it. But in fact, her beauty is extremely random, there are other similar, but not so beautiful examples:

(We can give you a hint for solving these problems, and here are the answers .)
If I show you the Yamamoto puzzle, then it will be interesting for you to solve it, because it is beautiful, but if I show you the second puzzle, then it may not interest you at all . I think Kaprekar’s problem is similar to Yamamoto’s number search problem. We like these puzzles because they are beautiful. And for the same reason, it seems to us that there should be more to them than a mere coincidence. Such misunderstandings have repeatedly led to scientific discoveries in mathematics and the science of the past.
Is it enough to know that all four-digit numbers are reduced to the number 6174 as a result of the Kaprekar function, but not to know why? Until now, no one could say with certainty that a unique fixed point for three- and four-digit numbers is just a random phenomenon. It seems such an amazing property that we can expect it to have some kind of big theorem from number theory. If we could answer this question, perhaps in the end it would turn out that we are just faced with a beautiful misunderstanding, but we hope that this is not so.
