Microcontroller random number generation

A lot has been written about random number generators, but almost always, when it comes to implementation, it is implied (or explicitly stated) that we are talking about x86 / x64 and other "adult" architectures. At the same time, forums devoted to the development of devices on microcontrollers are full of questions like “how can I generate a random number on% controllername%?”. Moreover, the range of answers extends from “see Google / Wikipedia” to “use the standard function”. Far from always this “standard function” exists and suits the developer in all respects, more often the other way around: either the numbers are far from random, the speed is too low, or the resulting code does not fit into free memory at all.
Let's try to figure out what random number generation algorithms are, how to choose a suitable one, and most importantly, what are the features of the implementation of these algorithms on controllers.

Assessment of "chance"

Applications for RNG can be found in a variety of ways, from toys to serious cryptography. Accordingly, the requirements for the generator also vary greatly. To assess the quality (level of "randomness") of the generator, there are special tests. Here are the most basic ones:

• Frequency test. It consists in counting the number of zeros and ones in a sequence of bits. Units and zeros should be approximately equal.
• Test for a sequence of identical bits. We search for rows of identical bits of the form 000 ... 0 or 111 ... 1. The distribution of frequencies encountered by the series, depending on their length, should correspond to such a distribution for a truly random signal.
• Spectral test. The discrete Fourier transform is applied to the original sequence. The resulting spectrum should not have significant peaks that would indicate the presence of periodic sequence properties.
• Autocorrelation test. The correlation value between copies of the sequence shifted relative to each other is calculated. The test allows you to find duplicate sections in a sequence.

There are special kits that include dozens of similar tests:
NIST - was used in the AES contest to evaluate encryption algorithms.
DIEHARD is one of the most rigorous sets available.

PRSP Algorithms

Any sequence generated by a hard-coded algorithm cannot be considered truly random, therefore, when speaking about algorithmic generators, the term pseudo-random sequence is used. Any pseudorandom number generator (PRNG) is looped sooner or later, another thing is that this “late” can occur in a few milliseconds, or maybe in a few years. The cycle length depends on the size of the internal state of the generator N (in fact, this is the amount of memory needed by the generator), and ranges from 2 ^{(N / 2)} to 2 ^N bits.
A huge number of PRSP algorithms were invented, but not all of them are convenient for implementation on microcontrollers. We are very limited in speed and available memory, many controllers do not support real arithmetic and even multiplication instructions. Bearing in mind such restrictions, we consider some well-known algorithms.

Linear congruent method

The next member of the sequence is calculated by the formula
X _{i + 1} = (aX _i + c) mod m
The number m determines the maximum period of the sequence, the integers a and c are the “magic” coefficients. It is reasonable to choose the number m equal to the power of two, in which case the reduction operation modulo reduces to discarding the most significant bits. In order to get the maximum period, the following conditions must be met:
- c and m must be coprime,
- a-1 must be a multiple of p for all prime divisors p of the number m ,
- if m is a multiple of 4 (and in our case it will be a multiple), then a-1 must be a multiple of 4.
There is one more subtlety: as a result, only the high bits of the state variable X should be taken, since for the lower bits the statistical randomness parameters much worse. A linear congruent algorithm is usually implemented as standard rand () in many libraries.

Pros:

• the maximum possible period for a given size of the state variable;
• fast enough;
• often already implemented in the compiler library.

Minuses:

• multiplication operation is required;
• not all bits are equally random.

Summary: A quick and easy algorithm for not-so-critical applications.

Fibonacci method with delays

This algorithm uses the relation
X _i = X _i-a - X _i-b ,
where the state variable X is an unsigned integer. The delay values a and b are taken not just any, but strictly determined; to achieve maximum quality, pairs (17.5), (55.24) or (97.33) are recommended. The greater the delay, the longer the period and the better the spectral properties of the sequence. On the other hand, for the generator to work, it is required to store max {a, b} of the previous numbers, which is not always acceptable. Also, to start the generator, you need max {a, b} numbers, which are usually obtained using a simple PRSP.

Pros:

• does not require multiplication operations;
• all bits of a random number are equivalent in statistical properties.

Minuses:

• requires a large amount of memory;
• requires a large array of numbers to run.

Summary: a very high-quality, but resource-intensive algorithm.

Linear Feedback Shift Register

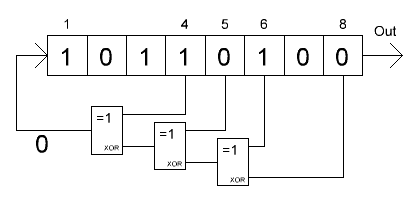
The state variable is stored in a register of length N. Generating the following state involves two steps:

1. The value of the bit C = X _i1 xor X _i2 xor ... X _{ik is calculated} , where i1, i2 ... ik are the register bit numbers, called taps .
2. Register is shifted by one bit to the right, the leftmost bit is set to On .

The output of the generator is the rightmost (or leftmost, or any other) bit of the register, that is, a pseudo-random sequence is generated one bit per iteration. With correctly selected branch numbers, the generator period will be 2 ^N - 1. “Minus one”, since there is a forbidden zero state of the register. Branch numbers for N from 3 to 168 can be found in this document .
In addition to the configuration described above, which, by the way, is called the Fibonacci configuration (not to be confused with the PRNG method of the same name!), There is a so-called. Galois configuration.

Instead of using the sum of bits of the tap sequence to generate the new leftmost bit, XOR each bit of the tap sequence with the rightmost bit is executed, then the entire register is cycled to the right. This scheme is more difficult to understand, but easier to implement, since all XOR operations can be performed simultaneously. In terms of the length of the period and the quality of the pseudo-random numbers, the Fibonacci and Galois schemes are equivalent.

Pros:

• very simple implementation, even arithmetic is not required, only bit operations and shifts;
• very fast algorithm (especially Galois scheme);
• good statistical properties.

Minuses:

• you need to check the initial value for inequality to zero.

Summary: a very fast and fairly high-quality algorithm.

Cryptographic Algorithms

For use in cryptography, the PRSP is presented with another essential requirement: irreversibility . All the above algorithms do not have this property: knowing several output values ​​of the PRNG, it is possible, having solved a simple system of equations, to find the parameters of the algorithm (the same “magic” constants a, b, c , etc.). And knowing the parameters, you can reproduce the entire pseudo-random sequence.
Any sufficiently strong block cipher can be used as a cryptographically robust PRNG algorithm. Choosing a secret key, you can get blocks of pseudorandom numbers by applying the algorithm to consecutive natural numbers. For N-bit block cipher period will be no more than 2 ^{of N} . The security of such a scheme depends entirely on the security of the key.
All modern cryptographic algorithms are tested for use as a PRNG, that is, using a certified algorithm, you do not need to specifically care about the statistical and spectral properties of the output stream. You only need to worry about the computational "gluttony" of cryptographic algorithms. If you need to perform a large number of encryption operations, it makes sense to choose a controller with hardware cryptographic units. Often in such controllers there is also a very good crypto-resistant hardware PRNG.

Sources of Entropy

As already mentioned, using only deterministic algorithms, it is impossible to generate a truly random number. Therefore, usually a combination of PRNG + an external source of entropy is used . The source of entropy is used to set the initial value for the PRNG, and the task of the latter is to ensure the spectral and statistical purity of the sequence. What can be used as a source of entropy? Yes, almost anything.

User activity

If the device interacts with the user in any way, it’s a pretty good solution to use the user’s entropy as a source. For example, the time it takes to press a button, measured accurate to the microsecond (or rather, its lower digits), is completely unpredictable. However, often the device must work autonomously, which means we are losing this wonderful channel of information.

Analog to digital converter

Many controllers have built-in ADCs. And in many controllers they are of very mediocre quality, made simply "to be." The low-order bits of the ADC result almost always contain significant noise, even if a constant voltage is measured. This can be used: connect the ADC input to the supply voltage through the divider, take a few dozen measurements, take the low-order bits - this is a great random number. If the ADC contains a built-in preamplifier, turn it on, it is also noisy.

Asynchronous Generators

You can use the period difference of two unsynchronized clocks. Most controllers contain, for example, a watchdog timer. To increase reliability, it is clocked from a separate generator, not connected in any way with the main clock signal. It is enough to count the number of ticks of the main clock signal for one watchdog period. If you select the periods so that the counter overflows many times during the measurement, you can get a fairly random number. The disadvantage of this method is that it requires a lot of time, up to several seconds.

Real time clock

If the circuit has a real-time clock , you can use their current readings to initialize the PRNG. For example, converting the current date / time to Unix time format , we immediately get 32 ​​bits, which will never be repeated, unless you take readings more often than once per second. Using real time gives uniqueness of values, but does not give any unpredictability, therefore it is better to combine this method with others.

RC circuit

If the controller does not have any peripheral devices other than I / O ports, you can do the following: one of the legs is connected through the capacitor to the ground, and through the resistor to the supply voltage. If the controller inputs have internal pull-up resistors, an external resistor is not needed.

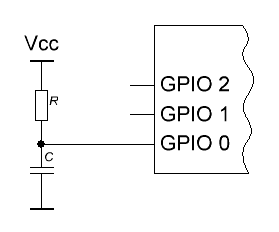
We output the signal “0” to this port - the capacitor is discharged. Switch the port to input mode - the capacitor starts charging. When the voltage across it reaches the threshold, the input will switch from state “0” to “1”. Charge time is highly dependent on many factors: supply voltage, drift of RC-circuit parameters, threshold instability, temperature, leakage, interference. By measuring it with sufficient accuracy and taking the least significant bits, you can get a good chance.

Hardware noise generator

For many serious applications (primarily cryptography), a more reliable source of entropy is required than the ones listed above. In such cases, digitizing the signal from a noise generator based on thermal , shot , or even quantum effects is used. The noisy element is usually a special diode or zener diode, the signal from which is amplified and fed to a comparator forming a binary bit stream.

In order that the threshold of the comparator does not affect the statistical properties of the received signal, two noise generators working on one comparator are used:

Conclusion

Finally, I’ll tell you a story from life. It began with the next question asked on the forum: “How do I generate a random number on the controller?”. The author of the question explained what he was doing as a term project a device emulating the throwing of a dice. After several unsuccessful attempts to understand the algorithms, the top starter shared his decision: he just threw a real die 1000 times and scored the entire free memory of the controller with the received numbers. The generator passed all the tests for "randomness" brilliantly, given that during the demonstration it spent less than a third of its "stock".
Therefore, such a solution also has the right to life, especially if very strict requirements are imposed on the randomness of numbers, but they are not required too often. Given the rapidly falling prices for memory, it may be prudent to equip the device with a USB flash drive with a “chaos margin” that is enough for the entire lifetime of the device.
Thank you for attention!

UPD1: As was rightly noted in the comments, if an attack on the RNG is supposed and the attacker has hardware access to the device, it is necessary to use external sources of entropy with great care, since it is not very difficult to replace the signal from an external source. Internal sources should be used, in addition to external sources.
It is also a good idea to accumulate entropy all your free time, and use it when you need to generate another random number. Usually in such cases the so-called Entropy pool - an array over which one of the functions of the PRNG is periodically performed, and where data from the sources of entropy are constantly mixed in.

UPD2: In many cases, it is useful to save the contents of the Entropy pool (sorry, I don’t know the normal Russian translation) in EEPROM so that after turning the device off and on it does not accumulate it again. This refers, first of all, to obtaining entropy by the method of asynchronous generators: under fairly stable conditions, the same sequence can be generated after each switching on.
If an attack is expected, take action against spoofing EEPROM content. If the controller allows, lock the read / erase / write using lock bits, when turned on, monitor the integrity of the EEPROM, at least using the simplest checksums.