Extraction from Direct of all information about competitors' campaigns
In continuation of the article by Evgeny Cheskidov Yandex. Direct. We analyze the competitive environment ” I want to show how, using not very complex calculations and the Yandex API, to get literally all the information about competitors' advertising campaigns from Direct. I must say right away that the idea has not yet been tested in practice, the very fact of the availability of all the information and, accordingly, the possibility of this calculation was shown by Cheskidov only yesterday, and the algorithm was born just now. But mathematically everything seems to converge. Caution, under the cut a lot of formulas.
i is the serial number of the advertisement on the "show all advertising results" page.
b [i] = bid, while the unknown maximum bid of the i-th ad. It follows from the Directive rules that
20 ≥ b [1] ≥ b [2] ≥ b [3] ≥ ... ≥ b [i] ≥ b [i + 1] ≥ ... ≥ 0.01 (1)
c [i] - is still unknown us the CTR of the i-th announcement, 0.01 ≤ c [i] ≤ 1.0
a [i] - the “effective rate” at which the ads are sorted in SERP, by definition
a [i] = b [i] ∙ c [i] (2)
o [i] - position of the i-th ad in SERP-e (search results page). The order in the SERP is determined by a, not b, therefore, in the general case, o [i] ≠ i. This fact is considered in detail in an article by Cheskidov.
r[j] is the inverse function to o [i], that is, r [o [i]] = o [r [i]] = i. Physically, this is the ad index i, which occupies the j-th position in SERP, if we consider that the ads with numbers j = 1 ... 3 are in the special placement, and with the numbers j = 4 ... 10 in the right block.
From the competition rules for Direct declarations in SERPa issuance, we know that
a [r [1]] ≥ a [r [2]] ≥ ... ≥ a [r [j]] ≥ a [r [j + 1]] ≥ ... ( 3)
s [i] is the number of the impression strategy for related key phrases selected for the i-th ad:
• s [i] = 0 if the phrase without quotes and negative keywords is used as a key phrase
• s [i] = 1 if you use a keyword phrase with negative keywords
• s [i] = 2 if you use a keyword phrase in quotation marks
The case s [i] = 2 can be determined by noticing the absence of an ad for a keyword with a nonexistent word, for example, [pink elephants fv243ae]. To determine the case s [i] = 1, you need to find in the Wordstat the most obvious (frequency) negative keyword for the query and check if there is an ad on demand with this negative keyword, for example [pink elephants for free].
From the “budget forecast” for each strategy s, one can extract the averaged values of the initial conditions b0, c0 and, accordingly, a0:
b0 [s, 1] - forecast of the price of the first place in special accommodation
b0 [s, 3] - forecast of the price of entry to special placement
c0 [s , 3] - forecast of CTR in special accommodation
b0 [s, 4] - forecast of first place price
c0 [s, 4] - forecast of CTR of first place
b0 [s, 10] - forecast of entry price for guaranteed impressions
c0 [s, 10] - forecast CTR in guaranteed impressions.
Once again, we note that these are average forecasts, and not real parameter values, that is,
b0 [s, i] ≠ b [i] for all i> 1
But it can be argued that the effective rate a [i] in the forecast is exactly equal to the real effective rate of the i-th place, that is,
a0 [s [i], i] = a [r [i]], and more specifically
a0 [s [3], 3] = a [r [3]] (4)
a0 [ s [4], 4] = a [r [4]] (5)
a0 [s [10], 10] = a [r [10]] (6)
Finally, denote by K [s] the total number of queries in month by keyword for each strategy.
How does a person view the results page? He reads the first ad, with some probability p clicks on it, otherwise he reads the second ad, again with some probability clicks, and so on. We translate this into the formula language and denote by Xi a discrete event equal to 1 if the user clicked on the i-th ad and 0 if he did not click:

Since thousands of users view SERP, such events are independent. Mathematicians proved that in such a model, the probability of a click on the i-th position obeys the law of geometric distribution and is equal to
P (n) = p ∙ (1-p) n , (7)
where n is the number of the advertisement, starting from zero, and p- This is a parameter that depends on a specific keyword phrase.
The P (n) function itself is not yet a CTR, since it only takes into account the position of the ad on the page. In Yandex.Direct, the CTR is also affected by the selection by which a particular ad is displayed (i.e., impression strategy), position history (accumulated CTR) and the quality of the ad itself. History can be accumulated by methodically scanning SERP. As for the quality of the ads themselves, it is approximately the same in competitive topics, and since users do not read the results and view it diagonally, it does not play a big role.
Translating from mathematical into Russian, an ad in the 8th position cannot have a CTR of 70% or at least 20%. And vice versa, of course, you can place a disgusting ad in the first place of the special placement and “crush it with money”, but whatever your budget is, as statistics are collected from users, the CTR of this ad will fall and you will inevitably fall first from the first place, and then from the shows in general.
So in this article, for simplicity, I will consider CTR as a function of position and strategy. Interested readers can take into account factors such as the history of position changes, the entry of a key phrase into the ad text, or the relevance of the ad text to the rest of the ads on the page.
It should be noted that there is still a slight irreparable discrepancy between theory and practice: in mathematics, the sequence is assumed to be infinite, and the actual output is limited. This leads to the fact that the actual CTR of the latest ads in the block is slightly overestimated relative to the theoretical probability.
In order to make it a little clear what was discussed in the previous paragraphs, I will give two graphs:
The first graph shows the CTR versus position from a report from Alexander Sadovsky :
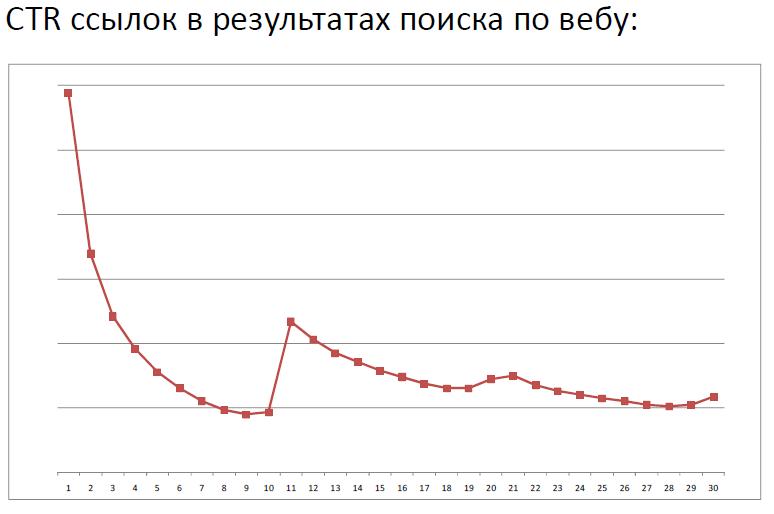
The second graph shows the probability function for a geometric distribution with different parameters p (from Wikipedia)

Knowing for each ad its position and strategy, we need to evaluate the expected CTR of this ad, that is, calculate the parameter p from formula (7).
For the right block, everything is simple, the expected CTR of the first place in the right block is given to us by Yandex, that is,
pr [s] = c0 [s, 4] (8)
which needs to be calculated for all strategies s.
Knowing pr, we can calculate the theoretical values of c1 for all i using the formula
c1 [s, r [i]] = pr [s] ∙ (1 - pr [s]) r [i] -4 (9)
For the upper block ( there another parameter p) is all a little more complicated, since Yandex does not disclose the CTR value for the first ad in special placement, but only for the third. You have to look for a reference book in mathematics and solve the cubic equation
p 3 - 2p 2+ p - c0 [s, 3] = 0 (10)
Further, similarly to (8), only the exponent will be r [i] -1.
We write expressions (1) and (3) as a system of ordinary inequalities
b [1] ≥ b [2]
b [2] ≥ b [3]
...
b [9] ≥ b [10]
b [r [1]] ∙ s [r [1]] ≥ b [r [2]] ∙ c [r [2]]
b [r [2]] ∙ s [r [2]] ≥ b [r [3]] ∙ c [r [3]]
...
b [r [9]] ∙ s [r [9]] ≥ b [r [9]] ∙ c [r [9]]
(for the case with N = 10 announcements)
Note: we won’t be able to to solve the system if there are more than 10 ads, we simply don’t see the “second page of the directive” and we don’t recognize the relationship between a [r [i]] for i> 10. Outsider ads will have to be thrown out of the calculations.
Add to the system the boundary conditions on b and c and the initial values given by equations (4) ... (6).
Thus, we obtain a system of second-order inequalities with 2N unknowns, 3N inequalities, and three equations. The property of this system is such that for each pair of unknowns b [i], c [i] there is a small hyperbolic region in which these parameters can change without violating the inequality conditions.
To resolve this uncertainty, we need to add additional restrictions on b and c in such a way that b [i] tend to zero while maintaining positions (no one will overpay for nothing), and c [i] tend to the theoretically expected values.
With these additional restrictions, we will not be able to find the real value of the maximum bids, but only the minimum necessary values so that the ads take the observed places. In practice, this means that if the most expensive ad has a bid of 10 cu, but really for the first place you need only 3.01 cu, we will find the value 3.01. But in our case, it doesn’t matter, because Yandex already tells us the largest bid for a keyword, and all other bids are consistently lower than the previous one.
We introduce the “penalty function” into the system - a measure showing how the approximate solution does not satisfy our conditions.
The structure of the penalty function will be something like this:
1. A large fine for non-fulfillment of inequalities (1) (ordering b [i]), a small fine for “overfulfillment” of these inequalities;
2. Large penalty for non-fulfillment of inequalities (2) (ordering a [i]), zero penalty for their fulfillment.
3. A very large fine for not fulfilling the boundary conditions on c [i]
4. A large fine for not fulfilling equations (4) ... (6).
5. Some penalty for deviating c [i] th from theoretical values.
Thus, we get the usual task of optimizing the penalty function, that is, finding values of b [i] and c [i] for which the value of the penalty function will be minimal. The search algorithms for such a solution have long been known from the branch of mathematics, which is called “optimization methods”. Using the appropriate algorithm, we will finally get the values b [i] and c [i], that is, bids and CTR for all competing ads.
Now the most interesting thing: knowing the bid, CTR, strategy and number of impressions K [s] for each ad, we can estimate the maximum monthly budget of each ad for this keyword. Knowing CTR and K [s] - estimate the number of clicks and, thus, the targeted traffic on the competitor’s website. And knowing the budget and the number of transitions, we can estimate the cost of each transition, that is, the quality of the advertising campaign settings. Knowing the quality of the advertising campaign, we can draw far-reaching conclusions, which, however, are no longer described by any mathematics)
Finally, knowing the semantic core of the subject area and connecting to the direct via the API, we can calculate the total budget of all advertising campaigns of competitors throughout the core in almost automatic mode. “Almost” - because the core and negative keywords still have to be selected manually.
And knowing the real budgets of all competitors ... well, you understand.
In general, Yandex provided all the information to play in Yandex.Direct with "open eyes."
Here is such an applied Data Mining in action.
1. To begin with, we introduce the following notation:
i is the serial number of the advertisement on the "show all advertising results" page.
b [i] = bid, while the unknown maximum bid of the i-th ad. It follows from the Directive rules that
20 ≥ b [1] ≥ b [2] ≥ b [3] ≥ ... ≥ b [i] ≥ b [i + 1] ≥ ... ≥ 0.01 (1)
c [i] - is still unknown us the CTR of the i-th announcement, 0.01 ≤ c [i] ≤ 1.0
a [i] - the “effective rate” at which the ads are sorted in SERP, by definition
a [i] = b [i] ∙ c [i] (2)
o [i] - position of the i-th ad in SERP-e (search results page). The order in the SERP is determined by a, not b, therefore, in the general case, o [i] ≠ i. This fact is considered in detail in an article by Cheskidov.
r[j] is the inverse function to o [i], that is, r [o [i]] = o [r [i]] = i. Physically, this is the ad index i, which occupies the j-th position in SERP, if we consider that the ads with numbers j = 1 ... 3 are in the special placement, and with the numbers j = 4 ... 10 in the right block.
From the competition rules for Direct declarations in SERPa issuance, we know that
a [r [1]] ≥ a [r [2]] ≥ ... ≥ a [r [j]] ≥ a [r [j + 1]] ≥ ... ( 3)
s [i] is the number of the impression strategy for related key phrases selected for the i-th ad:
• s [i] = 0 if the phrase without quotes and negative keywords is used as a key phrase
• s [i] = 1 if you use a keyword phrase with negative keywords
• s [i] = 2 if you use a keyword phrase in quotation marks
The case s [i] = 2 can be determined by noticing the absence of an ad for a keyword with a nonexistent word, for example, [pink elephants fv243ae]. To determine the case s [i] = 1, you need to find in the Wordstat the most obvious (frequency) negative keyword for the query and check if there is an ad on demand with this negative keyword, for example [pink elephants for free].
From the “budget forecast” for each strategy s, one can extract the averaged values of the initial conditions b0, c0 and, accordingly, a0:
b0 [s, 1] - forecast of the price of the first place in special accommodation
b0 [s, 3] - forecast of the price of entry to special placement
c0 [s , 3] - forecast of CTR in special accommodation
b0 [s, 4] - forecast of first place price
c0 [s, 4] - forecast of CTR of first place
b0 [s, 10] - forecast of entry price for guaranteed impressions
c0 [s, 10] - forecast CTR in guaranteed impressions.
Once again, we note that these are average forecasts, and not real parameter values, that is,
b0 [s, i] ≠ b [i] for all i> 1
But it can be argued that the effective rate a [i] in the forecast is exactly equal to the real effective rate of the i-th place, that is,
a0 [s [i], i] = a [r [i]], and more specifically
a0 [s [3], 3] = a [r [3]] (4)
a0 [ s [4], 4] = a [r [4]] (5)
a0 [s [10], 10] = a [r [10]] (6)
Finally, denote by K [s] the total number of queries in month by keyword for each strategy.
2. The statistical user model of Yandex
How does a person view the results page? He reads the first ad, with some probability p clicks on it, otherwise he reads the second ad, again with some probability clicks, and so on. We translate this into the formula language and denote by Xi a discrete event equal to 1 if the user clicked on the i-th ad and 0 if he did not click:

Since thousands of users view SERP, such events are independent. Mathematicians proved that in such a model, the probability of a click on the i-th position obeys the law of geometric distribution and is equal to
P (n) = p ∙ (1-p) n , (7)
where n is the number of the advertisement, starting from zero, and p- This is a parameter that depends on a specific keyword phrase.
The P (n) function itself is not yet a CTR, since it only takes into account the position of the ad on the page. In Yandex.Direct, the CTR is also affected by the selection by which a particular ad is displayed (i.e., impression strategy), position history (accumulated CTR) and the quality of the ad itself. History can be accumulated by methodically scanning SERP. As for the quality of the ads themselves, it is approximately the same in competitive topics, and since users do not read the results and view it diagonally, it does not play a big role.
Translating from mathematical into Russian, an ad in the 8th position cannot have a CTR of 70% or at least 20%. And vice versa, of course, you can place a disgusting ad in the first place of the special placement and “crush it with money”, but whatever your budget is, as statistics are collected from users, the CTR of this ad will fall and you will inevitably fall first from the first place, and then from the shows in general.
So in this article, for simplicity, I will consider CTR as a function of position and strategy. Interested readers can take into account factors such as the history of position changes, the entry of a key phrase into the ad text, or the relevance of the ad text to the rest of the ads on the page.
It should be noted that there is still a slight irreparable discrepancy between theory and practice: in mathematics, the sequence is assumed to be infinite, and the actual output is limited. This leads to the fact that the actual CTR of the latest ads in the block is slightly overestimated relative to the theoretical probability.
In order to make it a little clear what was discussed in the previous paragraphs, I will give two graphs:
The first graph shows the CTR versus position from a report from Alexander Sadovsky :

The second graph shows the probability function for a geometric distribution with different parameters p (from Wikipedia)

3. Calculation of theoretical CTR
Knowing for each ad its position and strategy, we need to evaluate the expected CTR of this ad, that is, calculate the parameter p from formula (7).
For the right block, everything is simple, the expected CTR of the first place in the right block is given to us by Yandex, that is,
pr [s] = c0 [s, 4] (8)
which needs to be calculated for all strategies s.
Knowing pr, we can calculate the theoretical values of c1 for all i using the formula
c1 [s, r [i]] = pr [s] ∙ (1 - pr [s]) r [i] -4 (9)
For the upper block ( there another parameter p) is all a little more complicated, since Yandex does not disclose the CTR value for the first ad in special placement, but only for the third. You have to look for a reference book in mathematics and solve the cubic equation
p 3 - 2p 2+ p - c0 [s, 3] = 0 (10)
Further, similarly to (8), only the exponent will be r [i] -1.
4. We assemble a system of equations.
We write expressions (1) and (3) as a system of ordinary inequalities
b [1] ≥ b [2]
b [2] ≥ b [3]
...
b [9] ≥ b [10]
b [r [1]] ∙ s [r [1]] ≥ b [r [2]] ∙ c [r [2]]
b [r [2]] ∙ s [r [2]] ≥ b [r [3]] ∙ c [r [3]]
...
b [r [9]] ∙ s [r [9]] ≥ b [r [9]] ∙ c [r [9]]
(for the case with N = 10 announcements)
Note: we won’t be able to to solve the system if there are more than 10 ads, we simply don’t see the “second page of the directive” and we don’t recognize the relationship between a [r [i]] for i> 10. Outsider ads will have to be thrown out of the calculations.
Add to the system the boundary conditions on b and c and the initial values given by equations (4) ... (6).
Thus, we obtain a system of second-order inequalities with 2N unknowns, 3N inequalities, and three equations. The property of this system is such that for each pair of unknowns b [i], c [i] there is a small hyperbolic region in which these parameters can change without violating the inequality conditions.
To resolve this uncertainty, we need to add additional restrictions on b and c in such a way that b [i] tend to zero while maintaining positions (no one will overpay for nothing), and c [i] tend to the theoretically expected values.
With these additional restrictions, we will not be able to find the real value of the maximum bids, but only the minimum necessary values so that the ads take the observed places. In practice, this means that if the most expensive ad has a bid of 10 cu, but really for the first place you need only 3.01 cu, we will find the value 3.01. But in our case, it doesn’t matter, because Yandex already tells us the largest bid for a keyword, and all other bids are consistently lower than the previous one.
We introduce the “penalty function” into the system - a measure showing how the approximate solution does not satisfy our conditions.
The structure of the penalty function will be something like this:
1. A large fine for non-fulfillment of inequalities (1) (ordering b [i]), a small fine for “overfulfillment” of these inequalities;
2. Large penalty for non-fulfillment of inequalities (2) (ordering a [i]), zero penalty for their fulfillment.
3. A very large fine for not fulfilling the boundary conditions on c [i]
4. A large fine for not fulfilling equations (4) ... (6).
5. Some penalty for deviating c [i] th from theoretical values.
Thus, we get the usual task of optimizing the penalty function, that is, finding values of b [i] and c [i] for which the value of the penalty function will be minimal. The search algorithms for such a solution have long been known from the branch of mathematics, which is called “optimization methods”. Using the appropriate algorithm, we will finally get the values b [i] and c [i], that is, bids and CTR for all competing ads.
5. PROFIT!
Now the most interesting thing: knowing the bid, CTR, strategy and number of impressions K [s] for each ad, we can estimate the maximum monthly budget of each ad for this keyword. Knowing CTR and K [s] - estimate the number of clicks and, thus, the targeted traffic on the competitor’s website. And knowing the budget and the number of transitions, we can estimate the cost of each transition, that is, the quality of the advertising campaign settings. Knowing the quality of the advertising campaign, we can draw far-reaching conclusions, which, however, are no longer described by any mathematics)
Finally, knowing the semantic core of the subject area and connecting to the direct via the API, we can calculate the total budget of all advertising campaigns of competitors throughout the core in almost automatic mode. “Almost” - because the core and negative keywords still have to be selected manually.
And knowing the real budgets of all competitors ... well, you understand.
In general, Yandex provided all the information to play in Yandex.Direct with "open eyes."
Here is such an applied Data Mining in action.
