Scanty nim
Hello!
Today I want to make out another classic problem for combinatorial games - a miserable one. Everyone knows that in the theory of games it with a normal ending occupies a central place, since all combinatorial games with a normal ending are reduced to it. Let's see how things are with the modification of the usual neem.
First, let's recall the formal definition of neem, the strategy of a game, and related theorems.
How to determine who will win in the optimal game of both rivals? This is what the Buton theorem tells us:
Let there be N heaps of neem, the number of stones in each of them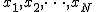 . Then the current position is losing if
. Then the current position is losing if  , where
, where - bitwise sum icon modulo 2 (xor). The proof of the theorem is based on the fact that from any position with a zero him-sum you can only go to a position with a non-zero (except for empty heaps), and from any position with a non-zero him-sum you can always go to a position with a zero. So, after the correct sequence of moves, the player with a non-zero him-sum always wins, because after his moves he leaves a zero him-sum, strictly reducing the number of stones, therefore, sooner or later he will take the last stones. Let's see how this theorem works on an example, let us have three heaps with the number of 3, 8, 15 stones in each. We write these numbers in a column in binary representation and calculate xor, it is equal to zero, so the second player, let's call him Y, is in the winning position. His strategy is in order to leave a position with zero sum in any way. Consider the possible moves, where Y adheres to his strategy and ultimately wins:
- bitwise sum icon modulo 2 (xor). The proof of the theorem is based on the fact that from any position with a zero him-sum you can only go to a position with a non-zero (except for empty heaps), and from any position with a non-zero him-sum you can always go to a position with a zero. So, after the correct sequence of moves, the player with a non-zero him-sum always wins, because after his moves he leaves a zero him-sum, strictly reducing the number of stones, therefore, sooner or later he will take the last stones. Let's see how this theorem works on an example, let us have three heaps with the number of 3, 8, 15 stones in each. We write these numbers in a column in binary representation and calculate xor, it is equal to zero, so the second player, let's call him Y, is in the winning position. His strategy is in order to leave a position with zero sum in any way. Consider the possible moves, where Y adheres to his strategy and ultimately wins:

It turns out that the strategy of the game in it is simple, it is even easier to determine the winner with the optimal strategy, now we turn to our task of a scanty neem. He has the same rules, with one exception: now the one who takes the last stone loses. Our task is to determine by the size of the heaps who will win with the optimal strategy. This time the game is scanty, which means it can not always be reduced to him, we do not have clear algorithms and approaches for solving this problem, they will have to be invented from scratch. In the solution I have proposed, we will try to reduce the miserable one to the usual one, in this case it is possible, but after some conclusions.
So, for starters, we need to find a position that will be advantageous for both a meager neem and a regular one. To do this, imagine the case when there are K piles of unit size and one heap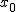 larger than one stone on the table . If we play the usual one, I will take the
larger than one stone on the table . If we play the usual one, I will take the 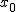 stones out, leaving one or zero so that after my move the opponent gets an even number of single piles, then I will win with any strategies; and if we play a miserable him, then I will leave an odd number of piles with one stone. Thus, we found a position in which the player wins in both games. Now we will divide all possible starting positions into two groups:
stones out, leaving one or zero so that after my move the opponent gets an even number of single piles, then I will win with any strategies; and if we play a miserable him, then I will leave an odd number of piles with one stone. Thus, we found a position in which the player wins in both games. Now we will divide all possible starting positions into two groups:
It is easy to see that in the first case, to give an answer, it is enough to check the parity of the number of heaps. In the case of parity, X wins, in the case of oddness Y. Now we consider the second case. You may notice that the optimal strategy here will be to reduce the game to the position we specified with K single heaps and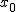 a bunch of size larger than one, let's call this position A. Moreover, no matter how the game goes, position A will be reached sooner or later by one of the players. Whoever falls into this position will win, both in a meager neem and in a normal neem, and it follows from this that we can check the initial position for profitability, as if we are playing in a regular one by calculating the xor of all the heaps. If xor is zero, then the first player to position A will be the second player, where nothing will interfere with him making a winning move in a meager neem. Otherwise, this move will go to X.
a bunch of size larger than one, let's call this position A. Moreover, no matter how the game goes, position A will be reached sooner or later by one of the players. Whoever falls into this position will win, both in a meager neem and in a normal neem, and it follows from this that we can check the initial position for profitability, as if we are playing in a regular one by calculating the xor of all the heaps. If xor is zero, then the first player to position A will be the second player, where nothing will interfere with him making a winning move in a meager neem. Otherwise, this move will go to X.
Thus, breaking the game into two cases, we easily defeat our task, here is its solution written in java:
There is no general approach to scanty games, sometimes they come down to games with a normal ending, sometimes not, here you just need quick wit and a little imagination)
Thank you for your attention.
Today I want to make out another classic problem for combinatorial games - a miserable one. Everyone knows that in the theory of games it with a normal ending occupies a central place, since all combinatorial games with a normal ending are reduced to it. Let's see how things are with the modification of the usual neem.
First, let's recall the formal definition of neem, the strategy of a game, and related theorems.
| Nimes is a mathematical game in which two players take turns taking items laid out in several piles. In one move, any number of items (greater than zero) can be taken from one pile. The player who takes the last item wins. |
How to determine who will win in the optimal game of both rivals? This is what the Buton theorem tells us:
Let there be N heaps of neem, the number of stones in each of them
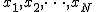 . Then the current position is losing if
. Then the current position is losing if  , where
, where - bitwise sum icon modulo 2 (xor). The proof of the theorem is based on the fact that from any position with a zero him-sum you can only go to a position with a non-zero (except for empty heaps), and from any position with a non-zero him-sum you can always go to a position with a zero. So, after the correct sequence of moves, the player with a non-zero him-sum always wins, because after his moves he leaves a zero him-sum, strictly reducing the number of stones, therefore, sooner or later he will take the last stones. Let's see how this theorem works on an example, let us have three heaps with the number of 3, 8, 15 stones in each. We write these numbers in a column in binary representation and calculate xor, it is equal to zero, so the second player, let's call him Y, is in the winning position. His strategy is in order to leave a position with zero sum in any way. Consider the possible moves, where Y adheres to his strategy and ultimately wins:
- bitwise sum icon modulo 2 (xor). The proof of the theorem is based on the fact that from any position with a zero him-sum you can only go to a position with a non-zero (except for empty heaps), and from any position with a non-zero him-sum you can always go to a position with a zero. So, after the correct sequence of moves, the player with a non-zero him-sum always wins, because after his moves he leaves a zero him-sum, strictly reducing the number of stones, therefore, sooner or later he will take the last stones. Let's see how this theorem works on an example, let us have three heaps with the number of 3, 8, 15 stones in each. We write these numbers in a column in binary representation and calculate xor, it is equal to zero, so the second player, let's call him Y, is in the winning position. His strategy is in order to leave a position with zero sum in any way. Consider the possible moves, where Y adheres to his strategy and ultimately wins:
It turns out that the strategy of the game in it is simple, it is even easier to determine the winner with the optimal strategy, now we turn to our task of a scanty neem. He has the same rules, with one exception: now the one who takes the last stone loses. Our task is to determine by the size of the heaps who will win with the optimal strategy. This time the game is scanty, which means it can not always be reduced to him, we do not have clear algorithms and approaches for solving this problem, they will have to be invented from scratch. In the solution I have proposed, we will try to reduce the miserable one to the usual one, in this case it is possible, but after some conclusions.
So, for starters, we need to find a position that will be advantageous for both a meager neem and a regular one. To do this, imagine the case when there are K piles of unit size and one heap
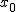 larger than one stone on the table . If we play the usual one, I will take the
larger than one stone on the table . If we play the usual one, I will take the 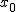 stones out, leaving one or zero so that after my move the opponent gets an even number of single piles, then I will win with any strategies; and if we play a miserable him, then I will leave an odd number of piles with one stone. Thus, we found a position in which the player wins in both games. Now we will divide all possible starting positions into two groups:
stones out, leaving one or zero so that after my move the opponent gets an even number of single piles, then I will win with any strategies; and if we play a miserable him, then I will leave an odd number of piles with one stone. Thus, we found a position in which the player wins in both games. Now we will divide all possible starting positions into two groups:- There are only a few piles on the table
- There are piles of size two or more on the table
It is easy to see that in the first case, to give an answer, it is enough to check the parity of the number of heaps. In the case of parity, X wins, in the case of oddness Y. Now we consider the second case. You may notice that the optimal strategy here will be to reduce the game to the position we specified with K single heaps and
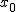 a bunch of size larger than one, let's call this position A. Moreover, no matter how the game goes, position A will be reached sooner or later by one of the players. Whoever falls into this position will win, both in a meager neem and in a normal neem, and it follows from this that we can check the initial position for profitability, as if we are playing in a regular one by calculating the xor of all the heaps. If xor is zero, then the first player to position A will be the second player, where nothing will interfere with him making a winning move in a meager neem. Otherwise, this move will go to X.
a bunch of size larger than one, let's call this position A. Moreover, no matter how the game goes, position A will be reached sooner or later by one of the players. Whoever falls into this position will win, both in a meager neem and in a normal neem, and it follows from this that we can check the initial position for profitability, as if we are playing in a regular one by calculating the xor of all the heaps. If xor is zero, then the first player to position A will be the second player, where nothing will interfere with him making a winning move in a meager neem. Otherwise, this move will go to X. Thus, breaking the game into two cases, we easily defeat our task, here is its solution written in java:
Copy Source | Copy HTML- int n = nextInt(), K = 0, nimSum = 0;
- for (int i= 0; i
- int size = nextInt();
- if (size == 1) K++;
- nimSum ^= size;
- }
- if (n - K >= 1)
- out.println(nimSum == 0 ? 'Y' : 'X');
- else
- out.println((K&1)==1 ? 'Y' : 'X');
-
There is no general approach to scanty games, sometimes they come down to games with a normal ending, sometimes not, here you just need quick wit and a little imagination)
Thank you for your attention.
