Search for similar images, parsing a single algorithm

I recently had to solve the problem of optimizing the search for duplicate images.
The existing solution runs on a fairly well-known Python library, Image Match , based on AN IMAGE SIGNATURE FOR ANY KIND OF IMAGE, authored by H. Chi Wong, Marshall Bern, and David Goldberg.
For several reasons, it was decided to rewrite everything to Kotlin, at the same time abandoning storage and searching in ElasticSearch, which requires significantly more resources, both iron and human, for support and administration, in favor of searching in the local in-memory cache.
To understand how it works, I had to immerse myself in the “reference” Python code, since the original work is sometimes not entirely obvious, and in a couple of places it makes me remember “how to draw an owl”. Actually, I want to share the results of this study, at the same time telling about some optimizations, both in terms of data volume and search speed. Maybe someone will come in handy.
Disclaimer: There is a possibility that I messed up somewhere, did it wrong or not optimally. Well, I will be glad to any criticism and comments. :)
How does it work:
- The image is converted to 8-bit black and white format (one dot is one byte in the value 0-255)
- The image is cropped in such a way as to discard 5% of the accumulated difference (more below) from each of the four sides. For example, a black frame around the image.
- A work grid is selected (9x9 by default), the nodes of which will serve as reference points of the image signature.
- For each reference point, on the basis of a certain area around it, its brightness is calculated.
- For each reference point, it is calculated how much it is brighter / darker than its eight neighbors. Five gradations are used, from -2 (much darker) to 2 (much brighter).
- All this “joy” unfolds in a one-dimensional array (vector) and is called by the image signature.
The similarity of the two images is checked as follows:
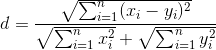
The lower the d, the better. In fact, d <0.3 is almost a guarantee of identity.
Now in more detail.
Step one
I think that talking about converting to grayscale makes little sense.
Second step
Let's say we have a picture like this:

It can be seen that there is a black frame of 3 pixels on the right and left and 2 pixels on the top and bottom, which we do not need at all in comparison.
The cutoff border is determined by this algorithm:
- For each column, we calculate the sum of the absolute differences of neighboring elements.
- We crop left and right the number of pixels whose contribution to the total cumulative difference is less than 5%.

We do the same for columns.
An important clarification: if the dimensions of the resulting image are insufficient for step 4, then we do not crop!
Step three
Well, everything is quite simple here, we divide the picture into equal parts and select the nodal points.

Fourth step
The brightness of the anchor point is calculated as the average brightness of all points in the square area around it. In the original work, the following formula is used to calculate the sides of this square:

Fifth step
For each reference point, the difference in its brightness with the brightness of its eight neighbors is calculated. For those points that lack neighbors (upper and lower rows, left and right columns), the difference is taken as 0.
Further, these differences are reduced to five gradations:
| xy | Value | Description |
|---|---|---|
| -2..2 | 0 | Identical |
| -50 ..- 3 | -1 | Darker |
| <-50 | -2 | Much darker |
| 3..50 | 1 | Brighter |
| > 50 | 2 | Much brighter |
It turns out something like this matrix:
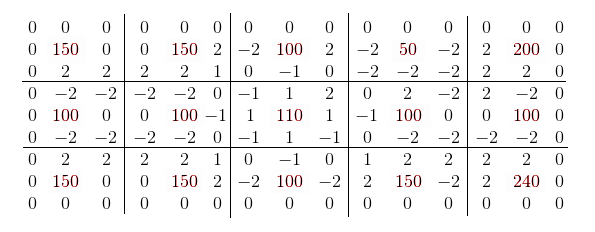
Sixth step
I think no explanation is needed.
And now about optimization
In the original work, it is rightly pointed out that from the resulting signature it is possible to completely erase zero values along the edges of the matrix, since they will be identical for all images.
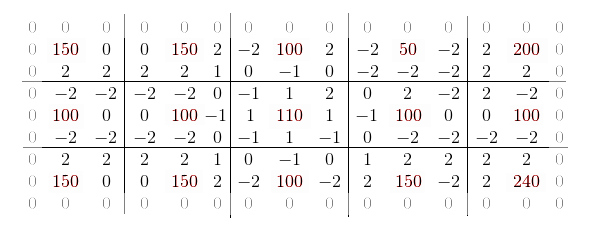
However, if you look closely, you can see that for any two neighbors their mutual gradations will be equal in absolute value. Therefore, in fact, you can safely throw out four duplicate values for each reference point, reducing the size of the signature by half (excluding side zeros).
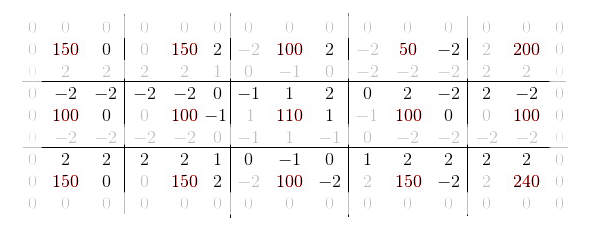
Obviously, when calculating the sum of squares, for each x there will definitely be an equal modulo x ' and the formula for calculating the norm can be written something like this (without going into reindexing):
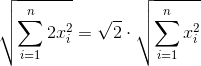
This is true both for the numerator and for both terms of the denominator.
Further in the original work, it is noted that three bits are enough to store each gradation. That is, for example, in the Unsigned Long will fit 21 gradations. This is a pretty big saving in size, but, on the other hand, it adds complexity when calculating the sum of the squares of the difference between the two signatures. I must say that this idea really hooked me with something and didn’t let go for a couple of days, until one evening it dawned on how to
We use such a scheme for storage, 4 bits per gradation:
| Graduation | Store as |
|---|---|
| -2 | 0b1100 |
| -1 | 0b0100 |
| 0 | 0b0000 |
| 1 | 0b0010 |
| 2 | 0b0011 |
Yes, only 16 gradations will fit into one Unsigned Long, against 21, but then the array of the difference of the two signatures will be calculated with one xor and 15 shifts to the right with the calculation of the number of bits set for each iteration of the shift. Those.
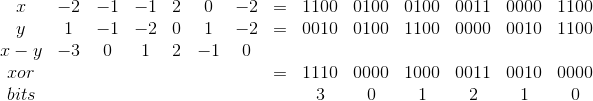
The sign does not matter to us, since all values will be squared.
In addition, if the threshold value of the distance is determined in advance, the values of which are not interesting to us anymore, then after dancing a little around the calculation formula, you can derive a rather lightweight filtering condition for a simple number of bits set.
More details about the optimization of this algorithm, with code examples, can be found in the previous article . Separately, I recommend reading comments on it - the Khabrovsk resident masyaman proposed several rather interesting methods for calculating, including packing gradations in three bits, using bit magic.
Actually, that's all. Thanks for attention. :)
