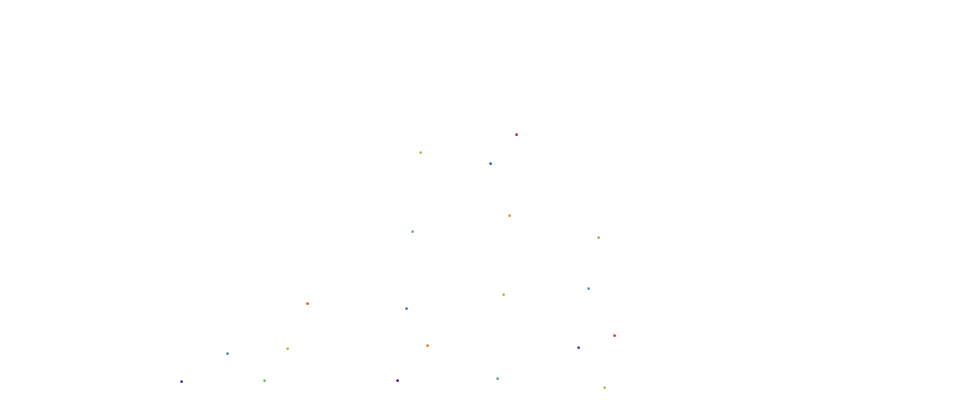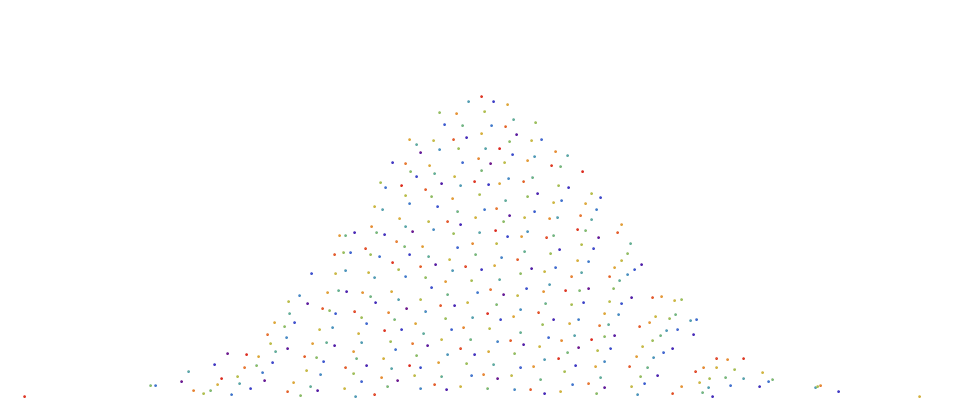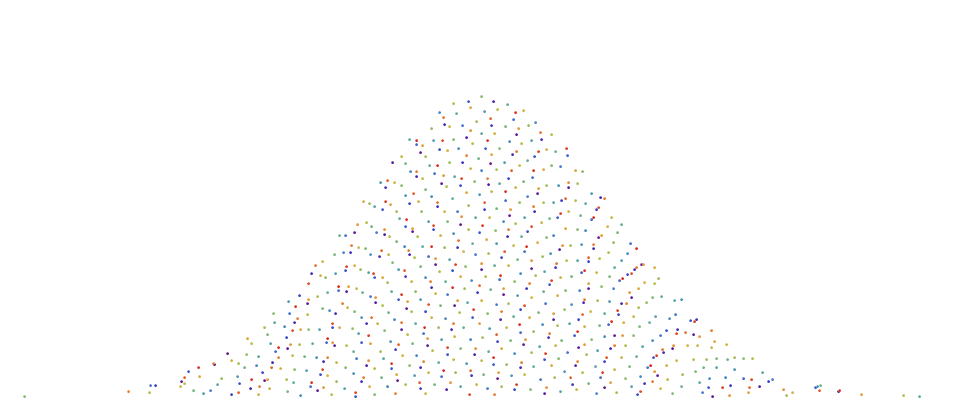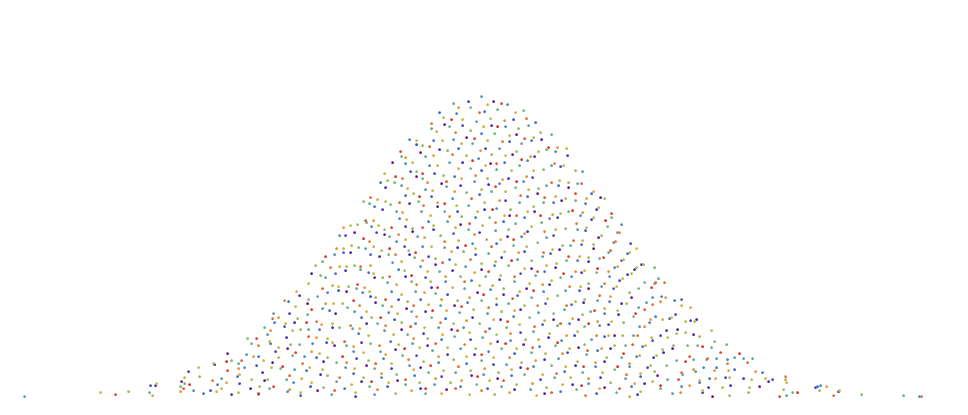Uniform distribution of points in a triangle
- Transfer
Most two-dimensional quasi-random methods are designed for unit square sampling. However, triangles are also very important in computer graphics. Therefore, I described a simple direct construction method for uniformly covering a sequence of points of a triangle of arbitrary shape.

Figure 1. A new direct method for constructing an open (infinite) quasi-random sequence with a low divergence in a triangle of arbitrary shape and size. The figure shows the distribution of points in fifteen random triangles for the first 150 points.
Low discrepancy sequences that uniformly sample / fill a square have been actively studied for nearly a hundred years. Most of these quasi-random sequences can be expanded to rectangles by simple stretching, without significantly damaging the discrepancy.
However, in this post we will consider an interesting and important extension of sequences with a low divergence into an arbitrary triangle.
As far as I could understand, very little attention was paid to the construction of sets of points and sequences uniformly distributed in a triangle. The noteworthy works of recent years by Basu [2014] , Pillands [2005] and Brandolini [2013] represent the main, if not the only articles on this topic.
These authors usually consider this problem from a very theoretical and analytical angle, and almost always solve it for a single regular triangle. In contrast to them, my post is mainly intended for the development of practical techniques in rendering graphics.
The post describes a simple method of direct construction, which does not require either acceptance / exclusion, or discarding or recursion; and most importantly, it can be applied to triangles of arbitrary size and shape.
The post consists of four sections:
You might think that placing 100 points in a square so that the minimum distance between adjacent points remains as large as possible will be easy. But what if you need to place 13 points? 47? What about 2019 points ?!
It turns out that sequences of points with low divergence provide a systematic way to solve this problem. There are many quasi-random sequences with a low divergence, from a simple Holton sequence to a more complex Sable sequence. Each of these sequences has its own advantages and disadvantages. For example, Holton sequences turn out to be more useful when placing objects in an area, because it has well-optimized local distance metrics such as nearest neighbors. The Sable sequence is prone to form more “crowded”, but the global distribution of points is very even, so it has excellent quadrature properties.
There is another sequence that I like to use, with excellent local as well as global properties. This is the sequence described in detail in my previous post “Unexpected efficiency of quasi-random sequences” .
described in detail in my previous post “Unexpected efficiency of quasi-random sequences” .
In short, we define an infinite two-dimensional sequence such that
such that
Read more about this special meaning. , which is often called a “plastic constant”, can be read on Wikipedia or Mathworld .
, which is often called a “plastic constant”, can be read on Wikipedia or Mathworld .
As a result, Figure 2 shows a comparison of different sequences with a low divergence (and a simple uniform random sample for comparison). As you can see, this random sample demonstrates the accumulation of points. Moreover, it contains areas that do not contain points at all (“white noise”), while a quasi-random sequence with a low divergence is a method of constructing a (infinite) sequence of points in a deterministic way so that at any stage the placed points are evenly distributed throughout space.
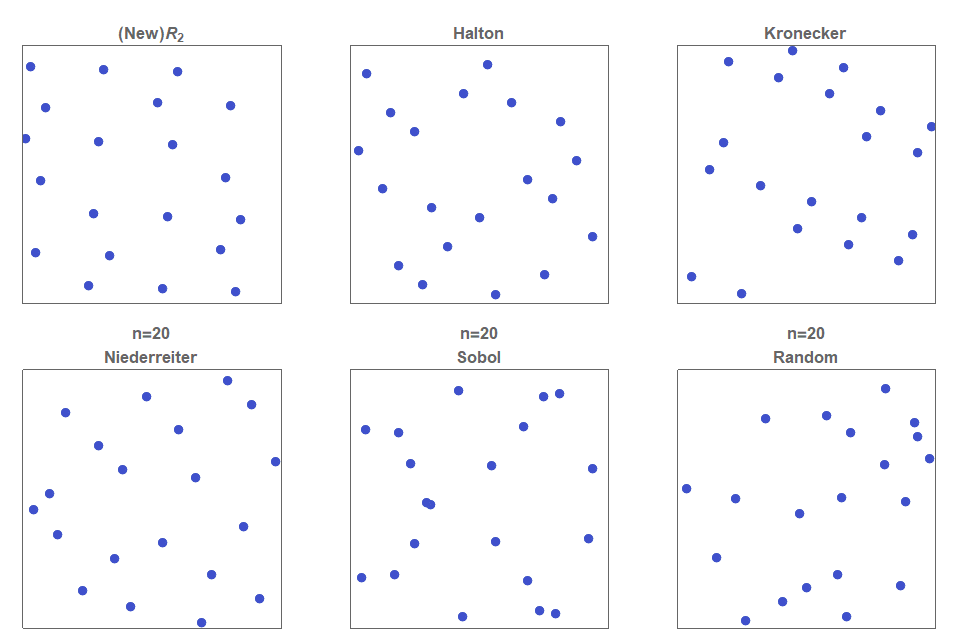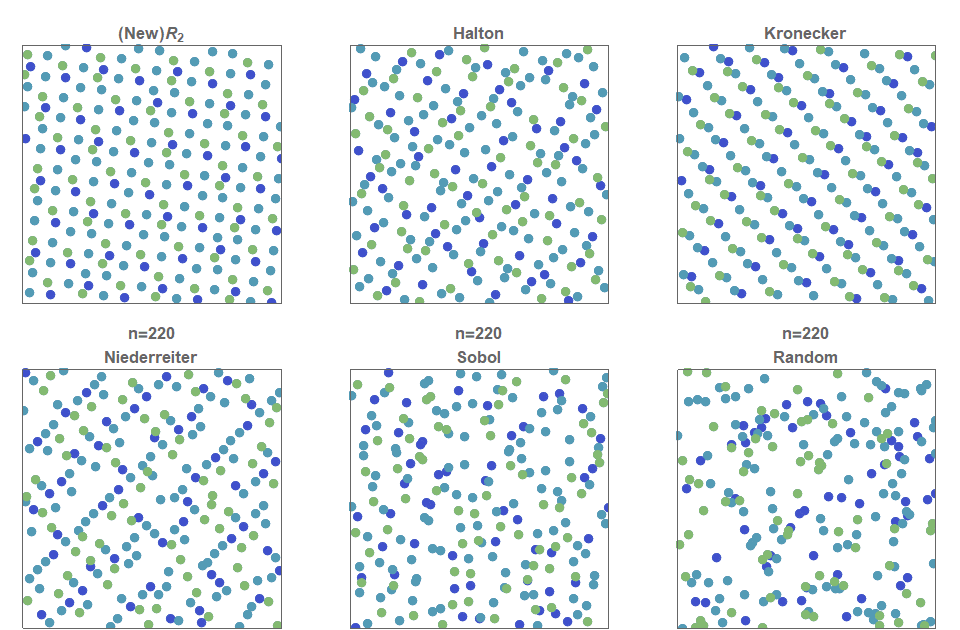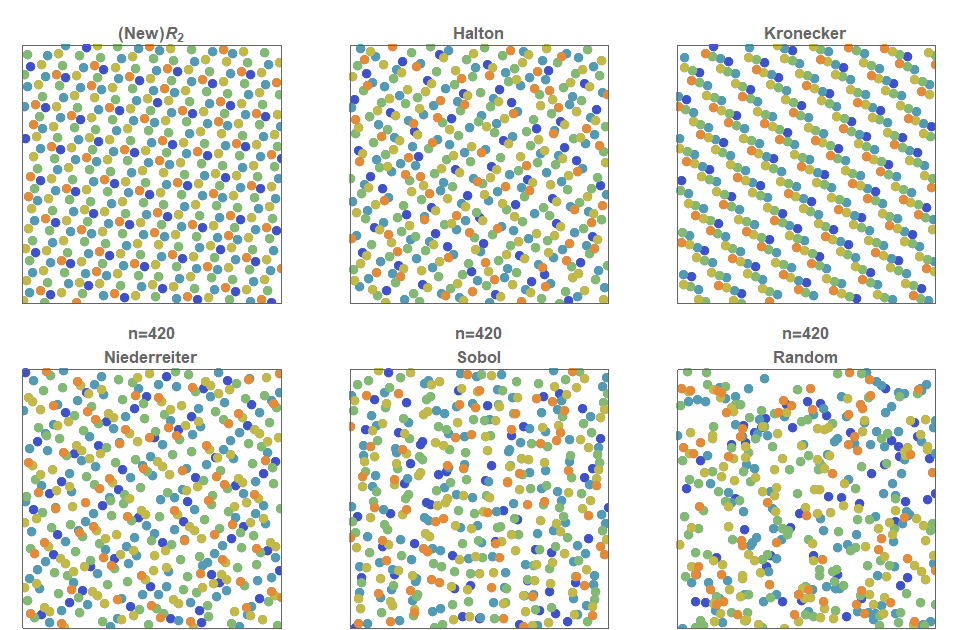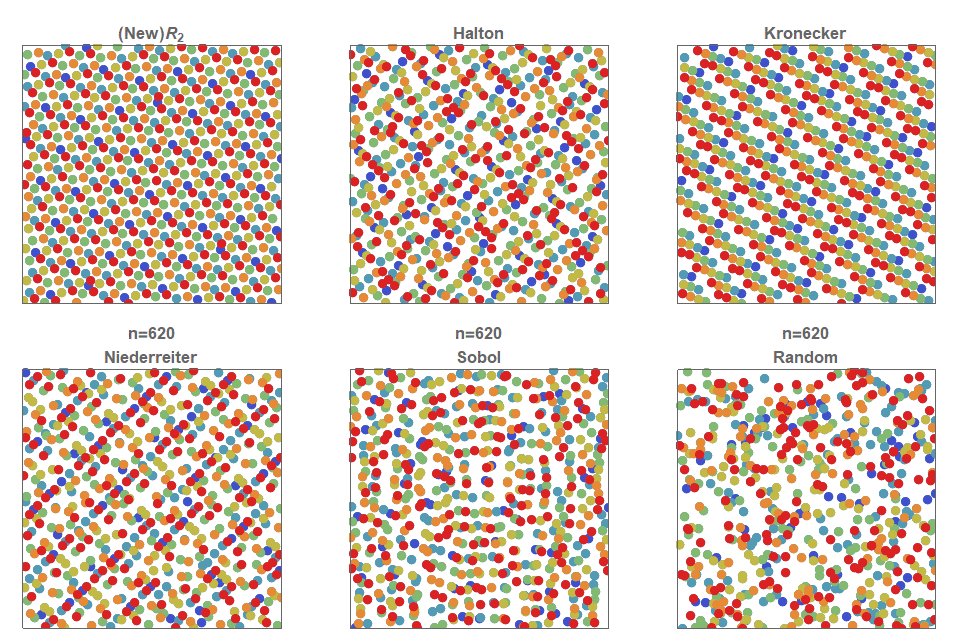
Figure 2. Illustration of the first 150 members of various low-divergence quasi-random sequences. Notice that they all create more evenly distributed points in space than a simple uniform random distribution (bottom left).
There are three well-known methods for ensuring uniform random sampling from a triangle:
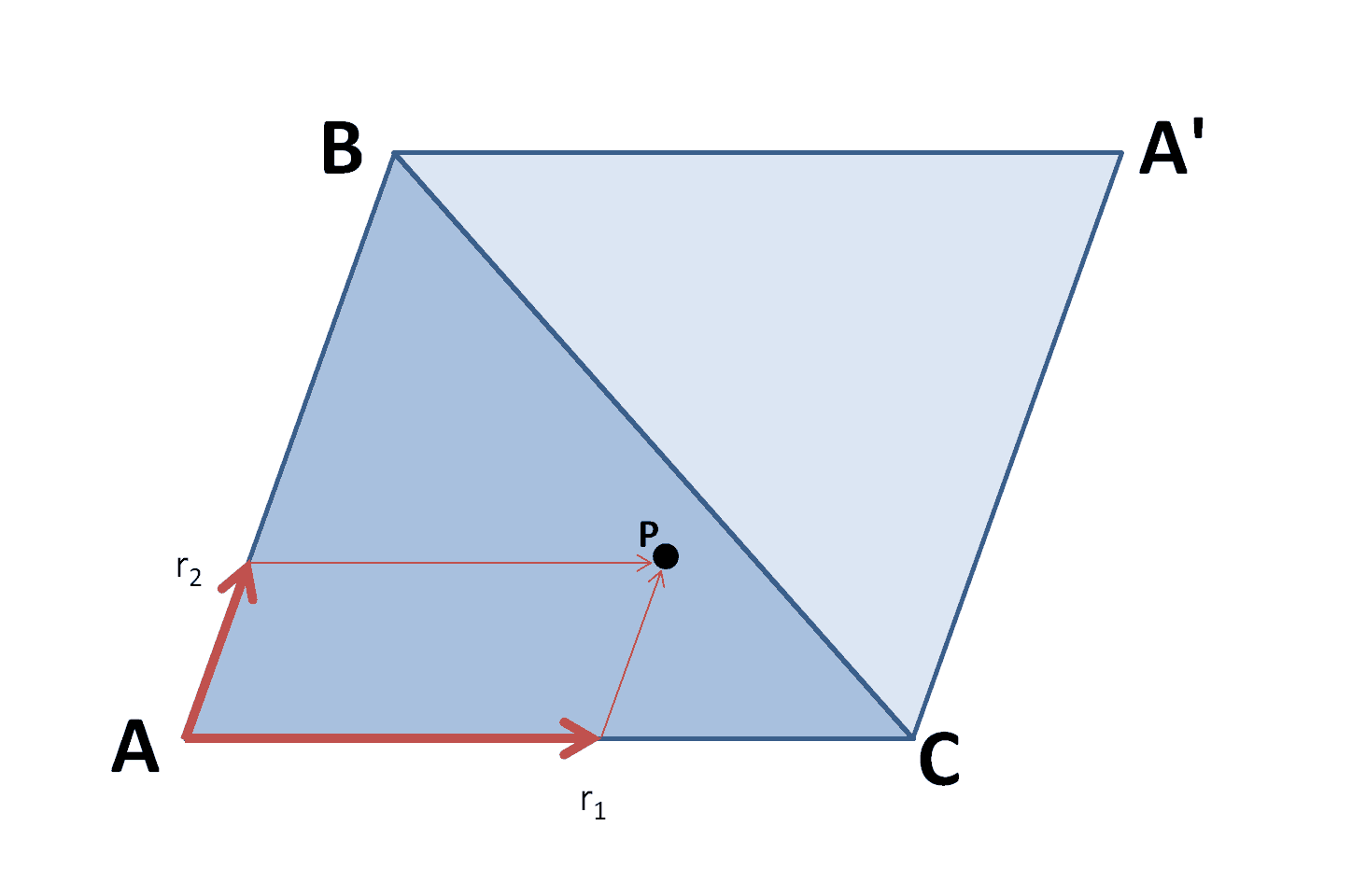
Figure 3. The parallelogram
method The parallelogram method is as follows.
For triangle consider a parallelogram
consider a parallelogram  .
.
For a point of a unit square set such a point
set such a point  , what
, what  .
.
This point will always be inside the parallelogram. However, if it appears in an additional triangle then we need to flip it back to the triangle
then we need to flip it back to the triangle  .
.
That is, if then
then  , but if
, but if  then
then  .
.
However, it is very important to understand that even though these methods provide uniform sampling from the triangle, this does not mean that such a transformation will preserve the uniform spatial arrangement (i.e., low divergence) of our quasi-random point distributions.
For example, in the case of the parallelogram method, reflection can often result in a point being very close to another existing point. Obviously, this destroys the low-divergence structure and appears as distortion / strip.
Similarly, the inverse probability distribution method applies nonlinear distortion to points. In Holton and Sable sequences, this means that two points very often push themselves very close together.
Figure 4 shows how well the low discrepancy is maintained in each of the various quasi-random sequences when transforming a region from a unit square to a triangle using the parallelogram method.

Figure 4. Comparison of the transformation of various quasi-random sequences in a triangle. Above is the Holton sequence, in the middle is the Sable sequence, below is the sequence . It can be seen that significant crowding of the points occurs in the Holton sequence, and significant band formation in the Sobol sequence. Compared to them, in sequence
. It can be seen that significant crowding of the points occurs in the Holton sequence, and significant band formation in the Sobol sequence. Compared to them, in sequence the points are distributed very evenly, and there is almost no noticeable crowding or stripes.
the points are distributed very evenly, and there is almost no noticeable crowding or stripes.
Of the three different triangulation methods and many different quasi-random sequences, the parallelogram method applied to the sequence method is the only combination that constantly creates results that are acceptable in terms of maintaining a low variance without distortion.
is the only combination that constantly creates results that are acceptable in terms of maintaining a low variance without distortion.
The excellent results of this combination can be examined in more detail in Figure 5.

Figure 5. You can see that the converted sequence provides a very simple but effective way to evenly distribute many of
provides a very simple but effective way to evenly distribute many of  points in the triangle. It works with acute-angled and obtuse-angled triangles. (Color indicates the arrangement).
points in the triangle. It works with acute-angled and obtuse-angled triangles. (Color indicates the arrangement).
The parallelogram method requires the choice of two sides of the triangle as basis vectors.
If vertices are marked in random order, then the patterns of points usually resemble those shown in Figure 6.
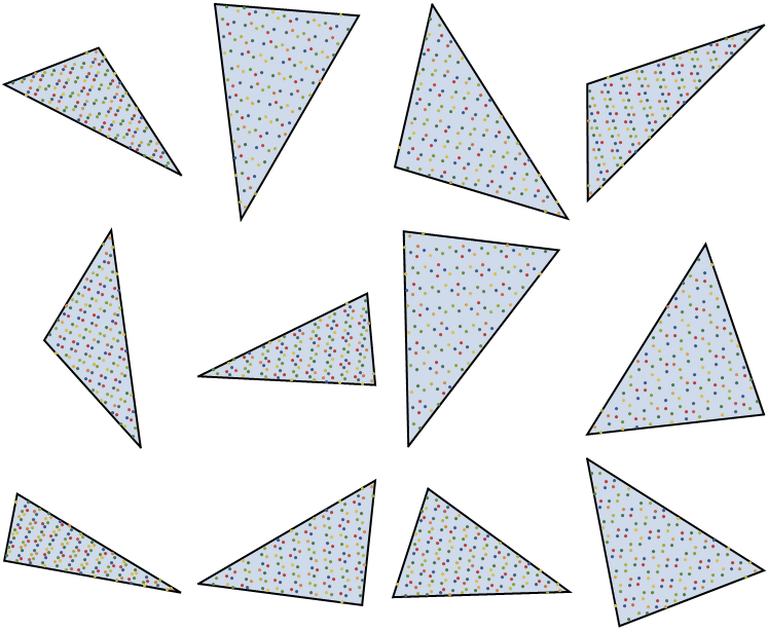
Figure 6. Patterns of points obtained by randomly choosing the order of vertices. Note that in most cases, distortion is clearly noticeable.
However, it turns out that with a careful choice of the order of the vertices, distortions can be significantly reduced. Most notably, if you label the triangle so that is the largest angle (i.e., the largest side is against it), then the sides
is the largest angle (i.e., the largest side is against it), then the sides  and
and  are used as two sides of a parallelogram.
are used as two sides of a parallelogram.
If we take this order, we get the point patterns shown in Figures 1, 4 and 5. Above,
however, even with a certain order of vertices, in some cases, distortion effects are still noticeable. They are most noticeable when one of the angles in the triangles is very small. In the case of obtuse triangles, when the smallest angle is less than 30 degrees, some distortion is noticeable, and in the case of acute-angled triangles, when the smallest angle is less than 20 degrees, distortion becomes visible. (If the sampled triangles are part of the Delaunay mesh, then such distortion problems can be minimal, because Delaunay triangulation is specifically designed to minimize the number of triangles with small angles.)
Unfortunately, the parallelogram technique cannot be used for other shapes, because it uses triangle symmetry. For some figures, good results can be obtained using the inverse probability distribution method. The following is an example of how the sequence with a low divergence, you can convert to a region bounded by a Gaussian curve while maintaining a uniform distance between points.
with a low divergence, you can convert to a region bounded by a Gaussian curve while maintaining a uniform distance between points.
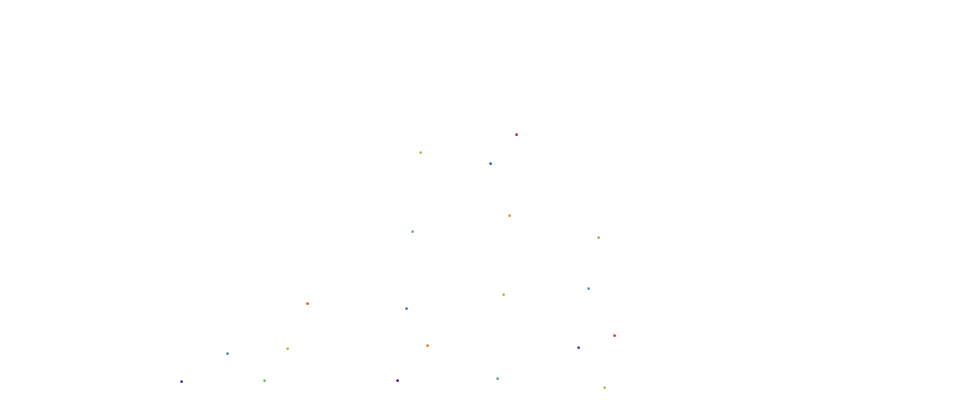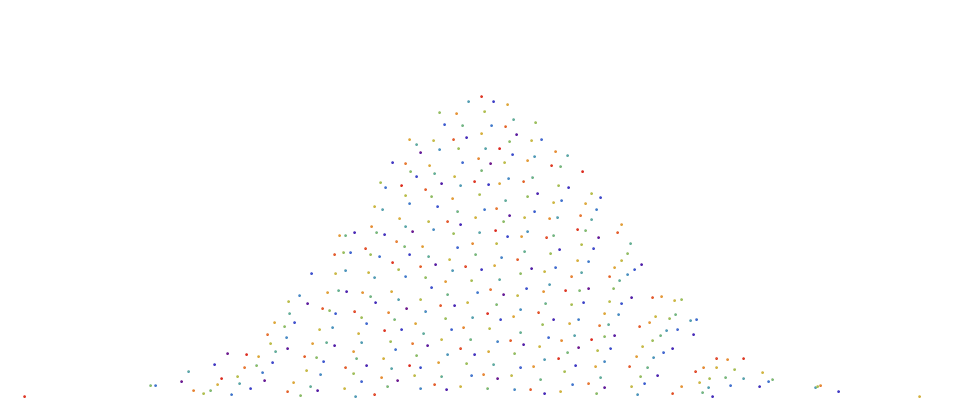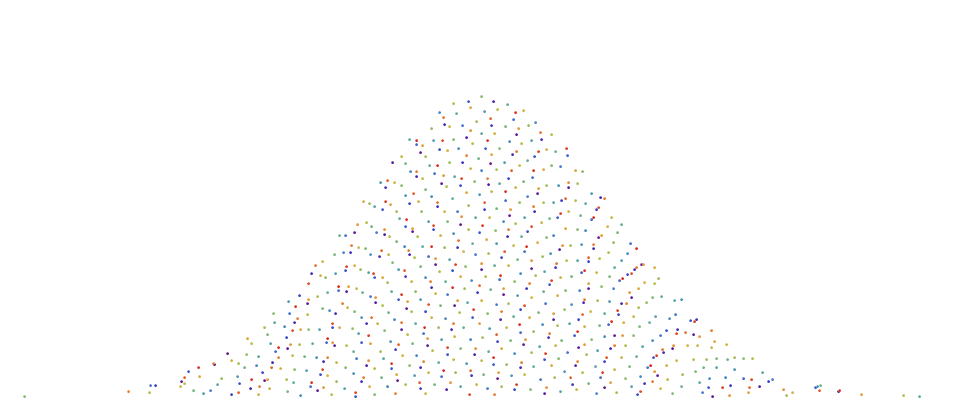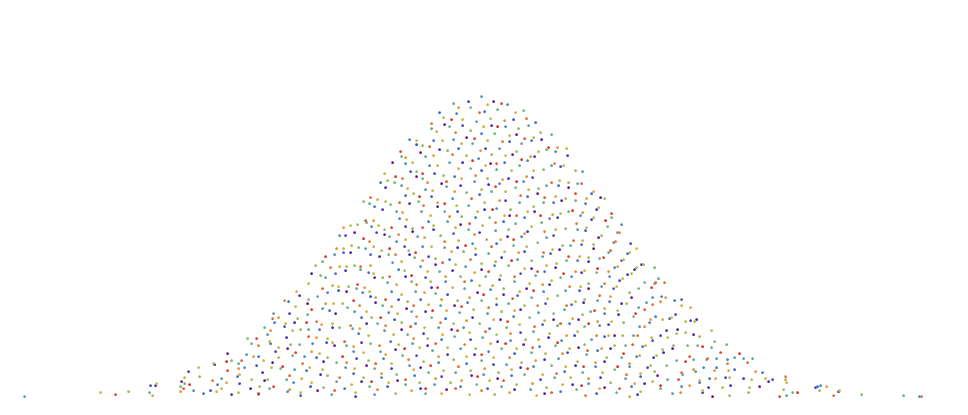

Figure 1. A new direct method for constructing an open (infinite) quasi-random sequence with a low divergence in a triangle of arbitrary shape and size. The figure shows the distribution of points in fifteen random triangles for the first 150 points.
Short review
Low discrepancy sequences that uniformly sample / fill a square have been actively studied for nearly a hundred years. Most of these quasi-random sequences can be expanded to rectangles by simple stretching, without significantly damaging the discrepancy.
However, in this post we will consider an interesting and important extension of sequences with a low divergence into an arbitrary triangle.
As far as I could understand, very little attention was paid to the construction of sets of points and sequences uniformly distributed in a triangle. The noteworthy works of recent years by Basu [2014] , Pillands [2005] and Brandolini [2013] represent the main, if not the only articles on this topic.
These authors usually consider this problem from a very theoretical and analytical angle, and almost always solve it for a single regular triangle. In contrast to them, my post is mainly intended for the development of practical techniques in rendering graphics.
The post describes a simple method of direct construction, which does not require either acceptance / exclusion, or discarding or recursion; and most importantly, it can be applied to triangles of arbitrary size and shape.
The post consists of four sections:
- Squared random sequences
- Overlay a unit square on a triangle.
- Distortion reduction
- Further generalizations
1. Quasi-random sequence of points
You might think that placing 100 points in a square so that the minimum distance between adjacent points remains as large as possible will be easy. But what if you need to place 13 points? 47? What about 2019 points ?!
It turns out that sequences of points with low divergence provide a systematic way to solve this problem. There are many quasi-random sequences with a low divergence, from a simple Holton sequence to a more complex Sable sequence. Each of these sequences has its own advantages and disadvantages. For example, Holton sequences turn out to be more useful when placing objects in an area, because it has well-optimized local distance metrics such as nearest neighbors. The Sable sequence is prone to form more “crowded”, but the global distribution of points is very even, so it has excellent quadrature properties.
There is another sequence that I like to use, with excellent local as well as global properties. This is the sequence
In short, we define an infinite two-dimensional sequence
Read more about this special meaning.
As a result, Figure 2 shows a comparison of different sequences with a low divergence (and a simple uniform random sample for comparison). As you can see, this random sample demonstrates the accumulation of points. Moreover, it contains areas that do not contain points at all (“white noise”), while a quasi-random sequence with a low divergence is a method of constructing a (infinite) sequence of points in a deterministic way so that at any stage the placed points are evenly distributed throughout space.

Figure 2. Illustration of the first 150 members of various low-divergence quasi-random sequences. Notice that they all create more evenly distributed points in space than a simple uniform random distribution (bottom left).
2. The imposition of a unit square on a triangle
There are three well-known methods for ensuring uniform random sampling from a triangle:
- parallelogram method ,
- Kramer’s method and
- inverse probability distribution method.

Figure 3. The parallelogram
method The parallelogram method is as follows.
For triangle
For a point of a unit square
This point will always be inside the parallelogram. However, if it appears in an additional triangle
That is, if
However, it is very important to understand that even though these methods provide uniform sampling from the triangle, this does not mean that such a transformation will preserve the uniform spatial arrangement (i.e., low divergence) of our quasi-random point distributions.
For example, in the case of the parallelogram method, reflection can often result in a point being very close to another existing point. Obviously, this destroys the low-divergence structure and appears as distortion / strip.
Similarly, the inverse probability distribution method applies nonlinear distortion to points. In Holton and Sable sequences, this means that two points very often push themselves very close together.
Figure 4 shows how well the low discrepancy is maintained in each of the various quasi-random sequences when transforming a region from a unit square to a triangle using the parallelogram method.

Figure 4. Comparison of the transformation of various quasi-random sequences in a triangle. Above is the Holton sequence, in the middle is the Sable sequence, below is the sequence
Of the three different triangulation methods and many different quasi-random sequences, the parallelogram method applied to the sequence method
The excellent results of this combination can be examined in more detail in Figure 5.

Figure 5. You can see that the converted sequence
3. Other aspects
Distortion
The parallelogram method requires the choice of two sides of the triangle as basis vectors.
If vertices are marked in random order, then the patterns of points usually resemble those shown in Figure 6.

Figure 6. Patterns of points obtained by randomly choosing the order of vertices. Note that in most cases, distortion is clearly noticeable.
However, it turns out that with a careful choice of the order of the vertices, distortions can be significantly reduced. Most notably, if you label the triangle so that
If we take this order, we get the point patterns shown in Figures 1, 4 and 5. Above,
however, even with a certain order of vertices, in some cases, distortion effects are still noticeable. They are most noticeable when one of the angles in the triangles is very small. In the case of obtuse triangles, when the smallest angle is less than 30 degrees, some distortion is noticeable, and in the case of acute-angled triangles, when the smallest angle is less than 20 degrees, distortion becomes visible. (If the sampled triangles are part of the Delaunay mesh, then such distortion problems can be minimal, because Delaunay triangulation is specifically designed to minimize the number of triangles with small angles.)
Other shapes
Unfortunately, the parallelogram technique cannot be used for other shapes, because it uses triangle symmetry. For some figures, good results can be obtained using the inverse probability distribution method. The following is an example of how the sequence