mzavatsky February 11, 2016 at 14:37

Kinematics of a Delta Robot

From the sandbox

Back in 2009, I got excited about building my own industrial robot that could do something useful (namely, sort small parts on a conveyor belt). I must say right away that I built a robot (the result you see in the title photo), and at the same time, as a by-product, I wrote a short article about the kinematics of delta robots on the forum TrossenRobotics - an American seller of robot parts kits. They just held a competition for authors at that time. Of course, I did not win the competition, but the article in English remained. Several times I tried to translate it into my native language, but I managed to complete what I started only now.

If you want to build your model of a delta robot, or just to figure out how you can derive kinematic formulas for this type of robot (without going beyond the school curriculum in algebra and geometry) - welcome to cat. For those who do not really like theory, at the end of the article are examples of ready-made code in C.

What is a delta robot

The Swiss scientist Raymond Clavel invented the delta robot ( wiki ) in the early 1980s, the following is an illustration from the original US4976582 patent for “A device for moving and positioning an element in space”:

The robot consists of two platforms: a fixed upper base (1) and a small movable platform (8) connected by three levers. Each lever consists of two parts: the upper shoulder (4) is rigidly connected to the engine (3) located on the upper base, and the lower one is a parallelogram (5), in the corners of which the so-called universal joints (6, 7) ( wiki) that allow angles to change. Each parallelogram is connected to the upper arm by a hinge (16) so that its upper side always remains perpendicular to its arm and parallel to the plane of the upper base. Thanks to this, the movable platform of the robot attached to the lower sides of the parallelograms will also always be parallel to the upper base. We can control the position of the platform by changing the angle of rotation of the upper levers relative to the base of the robot using motors.

In the center of the lower platform (8), the so-called the working body (in English the term end effector is used) of the robot (9). This may be a manipulator, a gripping device or, for example, an extruder in the case of a 3D printer. Additionally, another engine (11) can be used, which provides rotation of the working body through the rod (14).

The main advantage of delta robots is speed: heavy engines are placed on a fixed base, only the levers and the lower platform move, which they try to make from light composite materials, thereby reducing their inertia. Here, for example, an article on Geektimes with a couple of very effective videos.

Task statement

To build your own delta robot, you need to learn how to solve two problems. In the first situation, we know the position to which we want to move the robot arm of our robot (for example, we want to grab a cookie that is on the conveyor at a point with coordinates (x, y, z) . To do this, we need to determine the angles at which we they must rotate the motors connected with the levers of the robot in order to set it in the correct position for gripping.The procedure for determining these angles is called the inverse (in some Russian-language sources the word “inverse” is used) kinematic problem.
In the second situation, we know the angles that the control motors of the robot are turned on (if we use servomotors, we can easily find the corners by reading the readings from the angle sensors), and we want to find the position of the robot platform in space (for example, to adjust its position) . This is a direct kinematic task.

We formalize both tasks. Both the fixed base of the robot and its moving platform can be represented as equilateral triangles: in the diagram below, they are painted in green and pink, respectively. The rotation angles of the robot arms relative to the base plane (they are also the rotation angles of the motors) are designated as Ѳ ₁ , Ѳ ₂ and Ѳ ₃ , and the coordinates of the point are E ₀located in the center of the mobile platform and in which the robot arm of our robot will be fixed in real life - like (x ₀ , y ₀ , z ₀ ) .

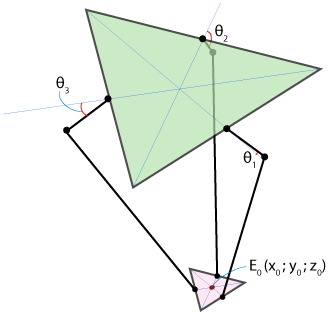
It turns out that we must come up with two functions:

f _inverse (x ₀ , y ₀ , z ₀ ) → (Ѳ ₁ , Ѳ ₂ , Ѳ ₃ ) to solve the inverse kinematic problem and
f _forward (Ѳ ₁ , Ѳ ₂ , Ѳ ₃ ) → (x ₀ , y ₀ , z ₀ ) to solve the direct kinematic problem.

Inverse kinematics

Let's set some key parameters that are determined by the geometric dimensions of our robot:

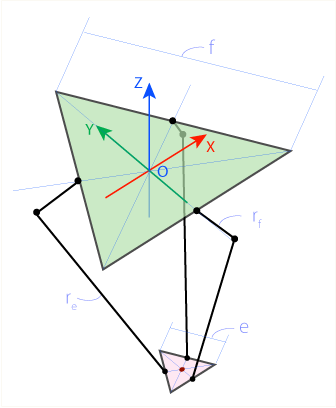
Let us denote the length of the side of the upper base f , the side of the lower platform e , the length of the upper arm of the lever r _f and the length of the lower arm (long side of the parallelogram) r _e . For calculations, we choose a coordinate system with a reference point that coincides with the geometric center of the upper triangle. The Z axis will be directed upward, so the z-coordinate of the moving platform will always be negative.

The design of the robot implies that the lever F ₁ J ₁ (see the figure below) can only rotate in the YZ plane , while describing a circle of radius r _f centered at a pointF ₁ (in this place it is attached to the engine). Unlike F ₁ , the nodes J ₁ and E ₁ use universal joints, thanks to which the shoulder E ₁ J ₁ can freely rotate relative to E ₁ , describing a sphere of radius r _e centered at the point E ₁ .

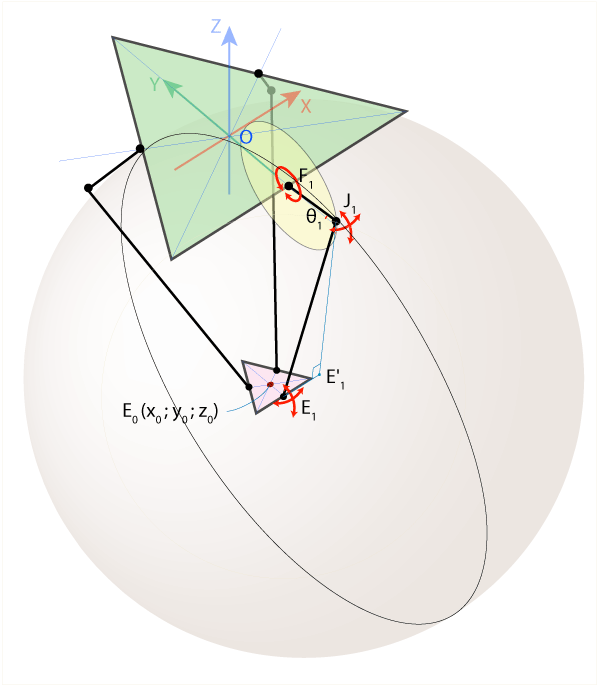
The intersection of this sphere and the YZ plane is a circle centered at the point E ' _{1 of} radius E' ₁ J ₁ , where the point E ' ₁ is located as the projection of the point E ₁ on the YZ plane . Then the point J ₁ will be at the intersection of two circles with centers at points E ' ₁ and F ₁ , and we can determine the radii of these circles. There is a slight subtlety: the circles intersect at two points, but we are only interested in one of them - with a smaller value of the y coordinate, because we want the arms of the robot to always stick out “elbows” out. Having thus determined the coordinates of the point J ₁ , we can easily find the angle угол _{1 of} interest to us .

For ease of perception, the projection of our three-dimensional image onto the YZ plane is shown below :

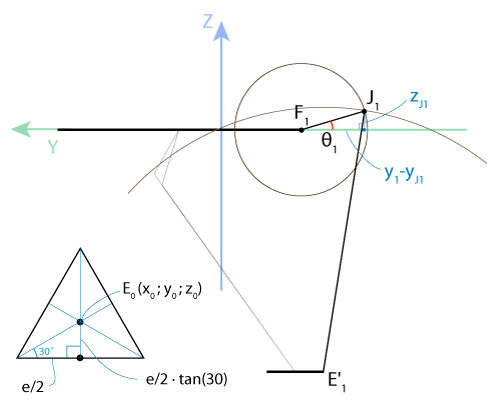
The lower platform is an equilateral triangle, the center of which is the point E ₀ (x ₀ , y ₀ , z ₀ ) . Mean distance

$E_0E_1 = {e \ over2} \ tan (30 ^ o) = {e \ over2 \ sqrt3},$

which gives us the following coordinates of the point E ₁ and its projection E ' ₁ on the plane YZ :

$E_1 (x_0, y_0- {e \ over2 \ sqrt3}, z_0) \ Rightarrow E'_1 (0, y_0- {e \ over2 \ sqrt3}, z_0)$

The distance E ₁ E ' ₁ = x ₀ , then, according to the Pythagorean theorem,

$E'_1J_1 = \ sqrt {E_1J_1 ^ 2-E_1E'_1 ^ 2} = \ sqrt {r_e ^ 2-x_0 ^ 2}$

Since the upper platform is also an equilateral triangle, the coordinates of the point F ₁ will be

$F_1 (0, {-f \ over {2 \ sqrt3}}, 0)$

To find the coordinates of the point J ₁ , which is the intersection of two circles, it is necessary to solve the system of equations:

$\ begin {equation *} \ begin {cases} (y_ {J_1} -y_ {F_1}) ^ 2+ (z_ {J_1} -z_ {F_1}) ^ 2 = r_f ^ 2 \\ (y_ {J_1} - y_ {E'_1}) ^ 2+ (z_ {J_1} -z_ {E'_1}) ^ 2 = r_e ^ 2-x_0 \ end {cases} \ end {equation *}$

We know the coordinates of the centers of circles, if we substitute them, we get the following expression:

$\ begin {equation *} \ begin {cases} (y_ {J_1} + {f \ over {2 \ sqrt3}}) ^ 2 + z_ {J_1} ^ 2 = r_f ^ 2 \\ (y_ {J_1} -y_0 + {e \ over {2 \ sqrt3}}) ^ 2+ (z_ {J_1} -z_0) ^ 2 = r_e ^ 2-x_0 \ end {cases} \ end {equation *}$

If you open the brackets and subtract one equation from the other, you can linearly express the z-coordinate of the point J _{1 in} terms of the y-coordinate, after which, substituting it in the second equation, we get the usual quadratic equation for y, from which two solutions we choose the smallest (more about this we talked above). And thus obtaining the coordinates of the point J ₁ , we find the angle

$\ theta_1 = \ arctan \ left ({z_ {J_1} \ over {y_ {F_1} -y_ {J_1}}} right$

All the expressions turned out to be quite simple due to the successful choice of the coordinate system: the lever arm F ₁ J ₁ always moves in the YZ plane , so we can simply ignore the x coordinate . To preserve this advantage when finding the two remaining angles Ѳ ₂ and Ѳ ₃ , we use the symmetry of the construction of the delta robot. First, turn our coordinate system 120 ° counterclockwise in the XY plane around the Z axis :

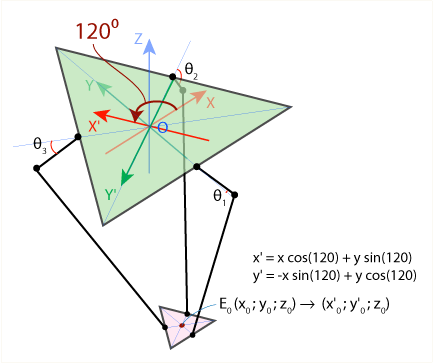
We got a new coordinate system X'Y'Z ' , and in this new system we can use our ready-made formulas to find the angle Ѳ ₂ . The only subtlety is that we must first recalculate the coordinates of the point E ₀ in the new frame of reference. This is easily done using the well-known formula (transformations when the system rotates around the origin), shown in the figure above. To find the angle Ѳ ₃it will also be necessary to rotate the original frame of reference, but now clockwise. This technique is very conveniently implemented in the form of a program: it is enough to write a function to calculate the angle Ѳ in the YZ plane, and then call it three times for each of the angles and reference systems.

Direct kinematics

Let's try to solve the inverse problem: now we know the angles Ѳ ₁ , Ѳ ₂ and Ѳ ₃ , and we want to find the coordinates (x ₀ , y ₀ , z ₀ ) of the point E ₀ located in the center of the moving platform of our robot. Knowing the angles, we can easily find the coordinates of the points J ₁ , J ₂ and J ₃ (see the figure below). Lever shoulders J ₁ E ₁ , J ₂ E ₂ and J ₃ E₃ can freely rotate around points J ₁ , J ₂ and J _3, respectively, forming in space three spheres with radii r _e .

We use a tricky technique: we displace the centers of each of these spheres from the points J ₁ , J ₂ , J ₃ in the XY plane in the direction of the Z axis , using the displacement vectors E ₁ E ₀ , E ₂ E ₀ and E ₃ E _0, respectively (in the figure they shown as red arrows). After this transformation, it turns out that all three spheres intersect at the point E ₀ , as shown in the figure below:

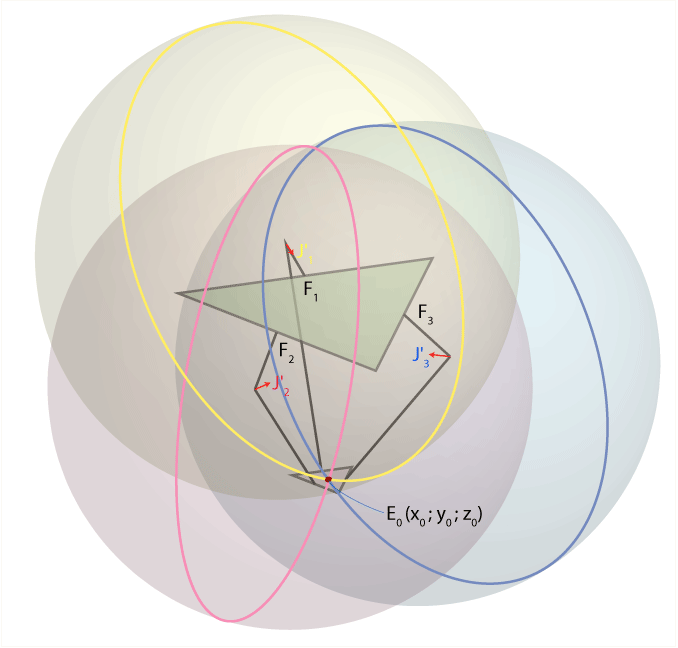
It turns out that to determine the coordinates (x ₀ , y ₀ , z ₀ ) of the point E _0, we must find the intersection point of three spheres, the radii and coordinates of the centers of which are known to us. In other words, we need to solve a system of three equations describing three-dimensional spheres:

$(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2 = r_e ^ 2,$

where (x _i , y _i , z _i ) are the coordinates of the centers of the spheres J ' ₁ , J' ₂ and J ' ₃ , which can be found as follows:

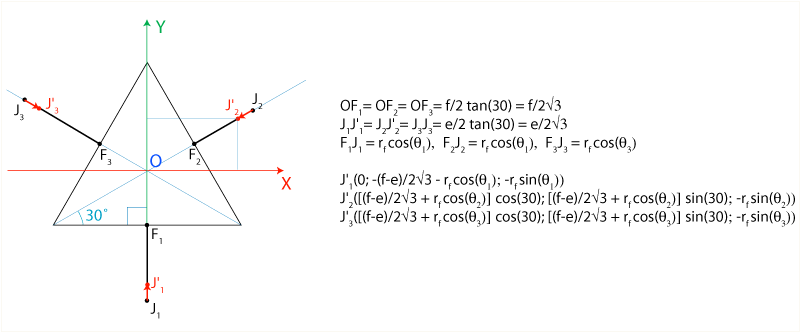
Below, to shorten the notation, I will use the notation (x ₁ , y ₁ , z ₁ ) , (x ₂ , y ₂ , z ₂ ) and (x ₃ , y as the coordinates of the points J ' ₁ , J' ₂ and J ' ₃₃ , z ₃ ), respectively. I also want to note that x ₁ = 0 (since the point J ' ₁ is in the YZ plane ). We get the following system of equations:

$\ begin {equation *} \ begin {cases} x ^ 2 + (y-y_1) ^ 2 + (z-z_1) ^ 2 = r_e ^ 2 \\ (x-x_2) ^ 2 + (y-y_2) ^ 2+ (z-z_2) ^ 2 = r_e ^ 2 \\ (x-x_3) ^ 2 + (y-y_3) ^ 2 + (z-z_3) ^ 2 = r_e ^ 2 \ end {cases} \ end { equation *} \ Rightarrow \ begin {equation *} \ begin {cases} x ^ 2 + y ^ 2 + z ^ 2-2y_1y-2z_1z = r_e ^ 2-y_1 ^ 2-z_1 ^ 2 \\ x ^ 2 + y ^ 2 + z ^ 2-2x_2x-2y_2y-2z_2z = r_e ^ 2-x_2 ^ 2-y_2 ^ 2-z_2 ^ 2 \\ x ^ 2 + y ^ 2 + z ^ 2-2x_3x-2y_3y-2z_3z = r_e ^ 2-x_3 ^ 2-y_3 ^ 2-z_3 ^ 2 \ end {cases} \ end {equation *}$

We introduce the notation

$w_i = x_i ^ 2 + y_i ^ 2 + z_i ^ 2$

and subtracting the second and third from the upper equation, as well as the third from the second, we get:

$\ begin {equation *} \ begin {cases} x_2x + (y_1-y_2) y + (z_1-z_2) z = (w_1-w_2) / 2 \\ x_3x + (y_1-y_3) y + (z_1-z_3) z = (w_1 -w_3) / 2 \\ (x_2-x_3) x + (y_2-y_3) y + (z_2-z_3) z = (w_2-w_3) / 2 \ end {cases} \ end {equation *}$

Subtracting the second from the first equation (thus reducing y ) and the third from the second (reducing x ), we can express x and y in terms of z :

$x = a_1z + b_1 \ qquad y = a_2z + b_2$

$a_1 = {1 \ over {d}} \ left [(z_2-z_1) (y_3-y_1) - (z_3-z_1) (y_2-y_1) \ right] \ qquad a_2 = - {1 \ over {d}} \ left [(z_2-z_1) x_3- (z_3-z_1) x_2 \ right]$

$b_1 = - {1 \ over {2d}} \ left [(w_2-w_1) (y_3-y_1) - (w_3-w_1) (y_2-y_1) \ right] \ qquad b_2 = {1 \ over {2d}} \ left [(w_2-w_1) x_3- (w_3-w_1) x_2 \ right]$

$d = (y_2-y_1) x_3- (y_3-y_1) x_2$

Now, substituting x and y , expressed through z , in the equation for the first circle (centered at the point J ' ₁ ), we obtain:

$(a_1 ^ 2 + a_2 ^ 2 + 1) z ^ 2 + 2 (a_1 + a_2 (b_2-y_1) -z_1) z + (b_1 ^ 2 + (b_2-y_1) ^ 2 + z_1 ^ 2-r_e ^ 2) = 0$

It remains to solve this quadratic equation (in the standard way, through the discriminant) to find z (we remember that we must choose the smallest of the two z !), And through it x and y .

Source code examples

Below are examples of functions for calculating the kinematics of a delta robot in C. The names of the variables correspond to the notation used in the article, angles theta1, theta2and are theta3indicated in degrees.

// размеры робота
// (обозначения см. на схеме)
const float e = 115.0;     // сторона подвижной платформы
const float f = 457.3;     // сторона неподвижного основания
const float re = 232.0;
const float rf = 112.0;
// тригонометрические константы
const float sqrt3 = sqrt(3.0);
const float pi = 3.141592653;    // PI
const float sin120 = sqrt3/2.0;
const float cos120 = -0.5;
const float tan60 = sqrt3;
const float sin30 = 0.5;
const float tan30 = 1/sqrt3;
// прямая кинематика: (theta1, theta2, theta3) -> (x0, y0, z0)
// возвращаемый статус: 0=OK, -1=несуществующая позиция
int delta_calcForward(float theta1, float theta2, float theta3, float &x0, float &y0, float &z0) {
    float t = (f-e)*tan30/2;
    float dtr = pi/(float)180.0;
    theta1 *= dtr;
    theta2 *= dtr;
    theta3 *= dtr;
    float y1 = -(t + rf*cos(theta1));
    float z1 = -rf*sin(theta1);
    float y2 = (t + rf*cos(theta2))*sin30;
    float x2 = y2*tan60;
    float z2 = -rf*sin(theta2);
    float y3 = (t + rf*cos(theta3))*sin30;
    float x3 = -y3*tan60;
    float z3 = -rf*sin(theta3);
    float dnm = (y2-y1)*x3-(y3-y1)*x2;
    float w1 = y1*y1 + z1*z1;
    float w2 = x2*x2 + y2*y2 + z2*z2;
    float w3 = x3*x3 + y3*y3 + z3*z3;
    // x = (a1*z + b1)/dnm
    float a1 = (z2-z1)*(y3-y1)-(z3-z1)*(y2-y1);
    float b1 = -((w2-w1)*(y3-y1)-(w3-w1)*(y2-y1))/2.0;
    // y = (a2*z + b2)/dnm;
    float a2 = -(z2-z1)*x3+(z3-z1)*x2;
    float b2 = ((w2-w1)*x3 - (w3-w1)*x2)/2.0;
    // a*z^2 + b*z + c = 0
    float a = a1*a1 + a2*a2 + dnm*dnm;
    float b = 2*(a1*b1 + a2*(b2-y1*dnm) - z1*dnm*dnm);
    float c = (b2-y1*dnm)*(b2-y1*dnm) + b1*b1 + dnm*dnm*(z1*z1 - re*re);
    // дискриминант
    float d = b*b - (float)4.0*a*c;
    if (d < 0) return -1; // несуществующая позиция
    z0 = -(float)0.5*(b+sqrt(d))/a;
    x0 = (a1*z0 + b1)/dnm;
    y0 = (a2*z0 + b2)/dnm;
    return 0;
}
// обратная кинематика
// вспомогательная функция, расчет угла theta1 (в плоскости YZ)
int delta_calcAngleYZ(float x0, float y0, float z0, float &theta) {
    float y1 = -0.5 * 0.57735 * f; // f/2 * tg 30
    y0 -= 0.5 * 0.57735 * e;       // сдвигаем центр к краю
    // z = a + b*y
    float a = (x0*x0 + y0*y0 + z0*z0 +rf*rf - re*re - y1*y1)/(2*z0);
    float b = (y1-y0)/z0;
    // дискриминант
    float d = -(a+b*y1)*(a+b*y1)+rf*(b*b*rf+rf);
    if (d < 0) return -1; // несуществующая точка
    float yj = (y1 - a*b - sqrt(d))/(b*b + 1); // выбираем внешнюю точку
    float zj = a + b*yj;
    theta = 180.0*atan(-zj/(y1 - yj))/pi + ((yj>y1)?180.0:0.0);
    return 0;
}
// обратная кинематика: (x0, y0, z0) -> (theta1, theta2, theta3)
// возвращаемый статус: 0=OK, -1=несуществующая позиция
int delta_calcInverse(float x0, float y0, float z0, float &theta1, float &theta2, float &theta3) {
    theta1 = theta2 = theta3 = 0;
    int status = delta_calcAngleYZ(x0, y0, z0, theta1);
    if (status == 0) status = delta_calcAngleYZ(x0*cos120 + y0*sin120, y0*cos120-x0*sin120, z0, theta2);  // rotate coords to +120 deg
    if (status == 0) status = delta_calcAngleYZ(x0*cos120 - y0*sin120, y0*cos120+x0*sin120, z0, theta3);  // rotate coords to -120 deg
    return status;
}

Used Books

I took all the key ideas about the kinematics of the delta robot from the work of prof. Paul Zsombor-Murray " Descriptive Geometric Kinematic Analysis of Clavel's" Delta "Robot ." I honestly admit that my mathematical training was not enough to understand it to the end, so a lot had to be deduced by myself.

Conclusion

Thanks to everyone who read this article to the end. I hope for someone it will be useful and inspire to create their own versions of the delta robot.

Tags: