Ask Ethan No. 41: A Date with a Remote Part of the Universe
- Transfer
The reader asks:
Of course, the speed of light is finite, and this fact can tell us a lot about some of the distant objects of the universe.

Here is the brightest star in the night sky: Sirius. It is located at a distance of 8.6 light years from us - that is, the light coming from it to us at the present time was emitted by it 8.6 years ago. It also means that if someone in the Sirius area could see us, he would see the Earth as it was 8.6 years ago.
Simply determine the age of the light from the star that we see. We measure the distance to the star, and, knowing the speed of light, we can calculate the time. This is true for any two points in the Universe that remain approximately at the same distance from each other during the passage of light between them.
You can also calculate the distances to different objects, knowing how they are arranged and work. For example, some types of stars change the luminosity with time, and there is a close relationship between the periods of brightness and their observed brightness.
If you can measure how much time a cycle of changing the luminosity of a star from bright to dim and vice versa takes, and you can determine the class and type of a given star, then you can tell how far away it is from us.

This method is suitable for measuring the distances of one star clusters and not very distant galaxies. After that, other details of the interrelations of different properties of galaxies (rotation, surface brightness fluctuations, velocity spread) allow us to calculate distances to even more distant objects of the Universe.

Among other things, we can use supernovae (in particular, the well-known type Ia supernovae with standard brightness), for very accurate measurements of distances to the most distant parts of the Universe. Even if they exploded billions of years ago.
But there is a problem with a simple measurement of the distance to objects and an attempt to calculate the elapsed time using the same method that we used, for example, in the case of Sirius. The problem is this: most of the Universe does not remain at the same distance from the Earth, even approximately. The universe is expanding!

The space itself is expanding - objects that are not connected to each other by gravity, with time move away from each other. This, of course, complicates the task, and for almost the entire 20th century it posed serious obstacles to determining how far we look into the past. After all, we could not just take a distant galaxy, measure the distance to it, and immediately find out:
To do this, you need to get more information than the simple current distance to the object.
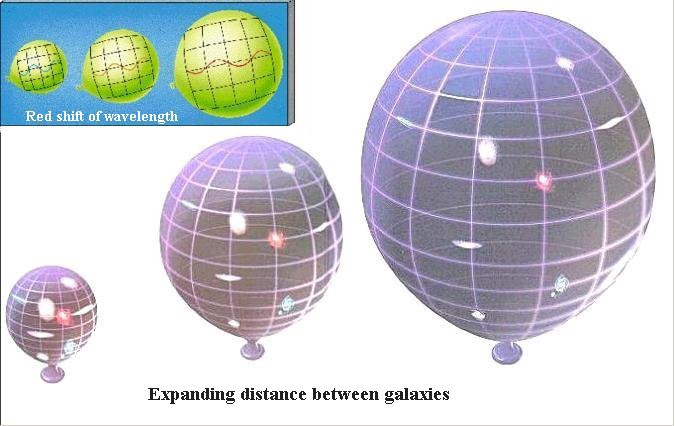
More precisely, two facts. Firstly, you need to know the full history of the expansion of the Universe, that is, the speed of expansion at the moment when the light leaves a distant object, the speed of expansion at the moment when we receive this light, and the speed of expansion between these two events.
Sounds complicated? In fact, everything is simpler. Einstein's general theory of relativity, talking about gravity, simply does not leave us with many options. If we can measure the current expansion rate (what we have been able to do since the 1920s), and can calculate the current energy content of the Universe, we can calculate the entire history of the expansion of the Universe from the Big Bang.
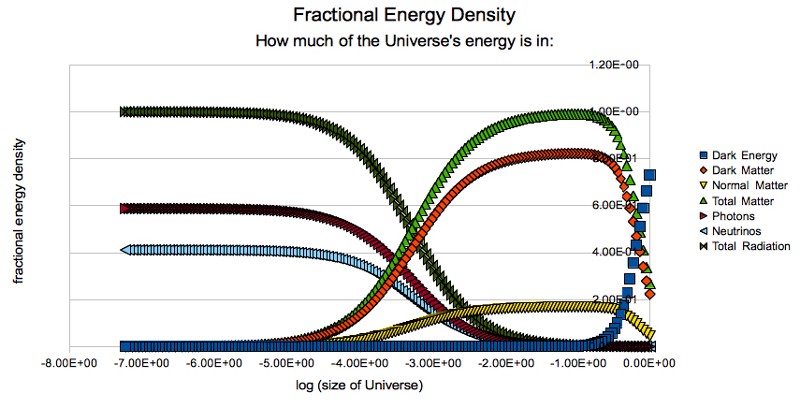
And the second fact? We need to measure the degree of redshift of the light that came to us from the object. As the structure of the universe expands, the wavelengths of light also stretch, and the light becomes redder. But since it is known that all light undergoes a redshift, and we know how atoms, stars and light behave, we can only take the appropriate measurements and find out how the redshift of light from a distant object occurs.
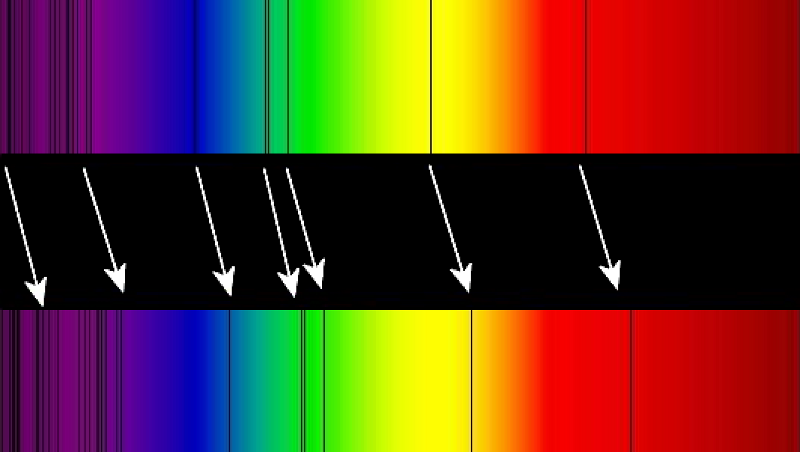
And that’s it. The distance to the object can be measured by various methods. The distance to a supernova is calculated through its light curve, as well as through the redshift (for a supernova, through spectral analysis).
We take these two facts, add the well-known history of the expansion of the Universe, and get the amount of time elapsed between the emission of the initial photon and its arrival in our eye.

This is how we learn how long ago this or that event in the Universe happened. Since we know that 13.82 billion years have passed since the Big Bang, we can calculate the age of the Universe at that moment when the light was emitted by any of the objects of interest to us.
I once attended a conversation about a supernova 12 billion years old, and when I answered the question “How is its age known?”, I said that this was due to the speed of light and the time it takes for it to travel a certain distance. But what if we were in another part of the universe? How would we know the age of this supernova? And then he would not be different?
Of course, the speed of light is finite, and this fact can tell us a lot about some of the distant objects of the universe.

Here is the brightest star in the night sky: Sirius. It is located at a distance of 8.6 light years from us - that is, the light coming from it to us at the present time was emitted by it 8.6 years ago. It also means that if someone in the Sirius area could see us, he would see the Earth as it was 8.6 years ago.
Simply determine the age of the light from the star that we see. We measure the distance to the star, and, knowing the speed of light, we can calculate the time. This is true for any two points in the Universe that remain approximately at the same distance from each other during the passage of light between them.

You can also calculate the distances to different objects, knowing how they are arranged and work. For example, some types of stars change the luminosity with time, and there is a close relationship between the periods of brightness and their observed brightness.
If you can measure how much time a cycle of changing the luminosity of a star from bright to dim and vice versa takes, and you can determine the class and type of a given star, then you can tell how far away it is from us.

This method is suitable for measuring the distances of one star clusters and not very distant galaxies. After that, other details of the interrelations of different properties of galaxies (rotation, surface brightness fluctuations, velocity spread) allow us to calculate distances to even more distant objects of the Universe.

Among other things, we can use supernovae (in particular, the well-known type Ia supernovae with standard brightness), for very accurate measurements of distances to the most distant parts of the Universe. Even if they exploded billions of years ago.
But there is a problem with a simple measurement of the distance to objects and an attempt to calculate the elapsed time using the same method that we used, for example, in the case of Sirius. The problem is this: most of the Universe does not remain at the same distance from the Earth, even approximately. The universe is expanding!

The space itself is expanding - objects that are not connected to each other by gravity, with time move away from each other. This, of course, complicates the task, and for almost the entire 20th century it posed serious obstacles to determining how far we look into the past. After all, we could not just take a distant galaxy, measure the distance to it, and immediately find out:
- how far she was from us the moment she let out the light
- how far is she from us now that this light has reached us
- how long did it take the light to cover this distance
To do this, you need to get more information than the simple current distance to the object.

More precisely, two facts. Firstly, you need to know the full history of the expansion of the Universe, that is, the speed of expansion at the moment when the light leaves a distant object, the speed of expansion at the moment when we receive this light, and the speed of expansion between these two events.
Sounds complicated? In fact, everything is simpler. Einstein's general theory of relativity, talking about gravity, simply does not leave us with many options. If we can measure the current expansion rate (what we have been able to do since the 1920s), and can calculate the current energy content of the Universe, we can calculate the entire history of the expansion of the Universe from the Big Bang.

And the second fact? We need to measure the degree of redshift of the light that came to us from the object. As the structure of the universe expands, the wavelengths of light also stretch, and the light becomes redder. But since it is known that all light undergoes a redshift, and we know how atoms, stars and light behave, we can only take the appropriate measurements and find out how the redshift of light from a distant object occurs.

And that’s it. The distance to the object can be measured by various methods. The distance to a supernova is calculated through its light curve, as well as through the redshift (for a supernova, through spectral analysis).
We take these two facts, add the well-known history of the expansion of the Universe, and get the amount of time elapsed between the emission of the initial photon and its arrival in our eye.

This is how we learn how long ago this or that event in the Universe happened. Since we know that 13.82 billion years have passed since the Big Bang, we can calculate the age of the Universe at that moment when the light was emitted by any of the objects of interest to us.
