Road safety issues, parse points
Road safety issues, parse points
How is it that a car with extremely simple controls (forward, backward, left, right) causes more than a million people to die annually? Obviously, this is not due to the complexity of driving, but to the problems of traffic management (speed limits, sequencing, etc.). We set the task to find a complete solution to every traffic problem. In this article we will consider the conceptual level, that is, what should be done to fully solve each problem. And how to implement it and how much it will cost, we will consider later.
1. The problem of lack of information
The first thing you need to make any management decision is the most complete information about the management object. And here we find out that the driver in the general case has no complete information and cannot even be theoretically. That is, even if we put all existing sensors on the car, we still will not get the full information necessary for making management decisions, for any money.

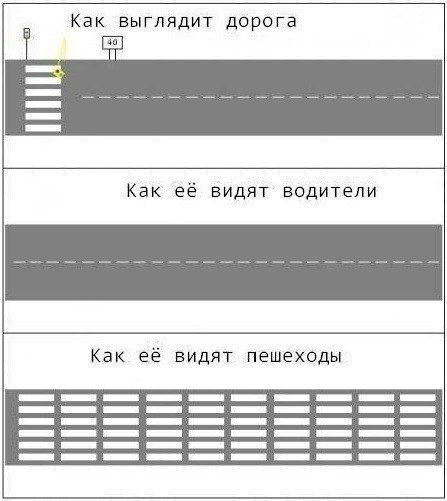
Do you need a camera showing if there is a pedestrian around the corner of the building?
From the car you can not see what happens even behind the nearest parked car, not to mention what is happening around the corner. And no sensors installed on the car (radar, lidar, and so on) will not help here. In part, promising Car-to-Car systems can help here, but they will not be able to completely solve the problem, as there will be cases when there are no other cars in the vicinity. Accordingly, we need an external (relative to the car) source of constant traffic information. That is, the infrastructure of complete and continuous monitoring of all roads and roadside territory. Unfortunately, even promising Car-to-I Car-to-X systems (vehicle-infrastructure and car-everything) cannot fully solve the problem either. Since, in principle, they do not possess completeness, which at some point will even reduce safety. For example, if there are no systems, then before a blind turn, the driver slows down, because he does not know what is there. And if the CarToX systems are installed on 99% of cars, then the driver thinks that since the information from around the corner has not arrived, it means that with a probability of 99% there is nothing dangerous there, and consequently, there is no need to slow down. It is clear that with a probability of 1% around the corner there may be a broken truck or a fallen tree. But since the probability of this is very small, many drivers will not slow down and, accordingly, will enter the truck at a higher speed than in the absence of additional information from CarToX. then the driver thinks that once the information has not been received from the corner, it means that with a probability of 99% there is nothing dangerous there, and consequently, there is no need to slow down. It is clear that with a probability of 1% around the corner there may be a broken truck or a fallen tree. But since the probability of this is very small, many drivers will not slow down and, accordingly, will enter the truck at a higher speed than in the absence of additional information from CarToX. then the driver thinks that once the information has not been received from the corner, it means that with a probability of 99% there is nothing dangerous there, and consequently, there is no need to slow down. It is clear that with a probability of 1% around the corner there may be a broken truck or a fallen tree. But since the probability of this is very small, many drivers will not slow down and, accordingly, will enter the truck at a higher speed than in the absence of additional information from CarToX.

The solution is obvious, it is necessary to remove the sensors from the car and evenly place it all along the road.
Thus, in order to fully solve the problem of limited and insufficient visibility from a car, it is necessary to create an external infrastructure for full continuous monitoring of all roads from the existing light poles. It is quite possible, we just put as many cameras as needed, and as often as needed.
2. Divination, in principle, cannot solve the problem of lack of information
Since the transport is moving at high speed and has great inertia, it is not enough just to know the exact coordinates of all road users. Need accurate information about their intentions. Existing traffic rules prescribe the driver to predict the actions of other road users. Obviously, if you are not Baba Vanga, then accurate predictions are impossible. Again, even promising CarToX systems cannot completely solve the problem, since, in principle, they do not have completeness and reliability. But the solution to this problem is well known. This is a central dispatch, for example, as in aviation. That is, instead of the existing principle “food as I want”, a permissive principle is introduced “in agreement with the dispatcher”. Thus, the dispatcher will have all accurate information about the intentions of all drivers.
3. The problem of completeness of information and its community

Sometimes just the beyond amount of information falls on the driver. And many signs should not just be recognized, but also remembered for their area of operation. And if the sign is not visible behind the branches of trees? And if he was blown away, or the homeless were taken for scrap? And the information should be GENERAL for all. That is, one-way traffic must be correctly displayed from two directions, otherwise a head-on collision is possible in which everyone will consider himself right. Another problem is that almost all signs are permanent. But speed limits are highly dependent on specific weather conditions, but the signs do not reflect this.
Well, the main question, why do you need all these signs? They are needed to somehow streamline the existing chaos. That is, these are crutches, which in no way solve the problem of chaos. But it is completely solved by a single reference system (central dispatching).
4. There are many forecasts and one plan.
The disadvantage of central dispatching systems is the exponential growth of scaling calculations. Since the addition of N + 1 participants makes it necessary to build predictions of its interaction with the already existing N participants. Thus, not only the dispatcher, but also a high-speed computer cannot cope with the dispatching of a huge number of cars. Another disadvantage of the central dispatch is its work in real time (any situation must be settled here and now). It is obvious that situations may arise by chance that, in principle, do not have a safe solution (the task of a trolley is not about an automatic car, but about existing chaotic traffic, which is sometimes impossible to solve even theoretically safely). But there is a complete solution! You just have to abandon the forecasts and go to the previously known and agreed road traffic plan. Thus, instead of a set of probabilistic forecasts of the road situation, we get one previously known road map. Moreover, computationally, this is a simple and long-solved task of constructing routes on a graph of the road network. It is even an order of magnitude simpler than the existing construction of routes, since it does not operate with probabilities, but has full information from the central dispatch. Even a home computer can cope with such a task, or rather many computers with a hierarchical structure of interconnections. Thus, AUTOMATIC central dispatching of all traffic in real time becomes possible. That is, the problem of lack of information is completely solved. instead of a set of probabilistic forecasts of the road situation, we get one previously known road map. Moreover, computationally, this is a simple and long-solved task of constructing routes on a graph of the road network. It is even an order of magnitude simpler than the existing construction of routes, since it does not operate with probabilities, but has full information from the central dispatch. Even a home computer can cope with such a task, or rather many computers with a hierarchical structure of interconnections. Thus, AUTOMATIC central dispatching of all traffic in real time becomes possible. That is, the problem of lack of information is completely solved. instead of a set of probabilistic forecasts of the road situation, we get one previously known road map. Moreover, computationally, this is a simple and long-solved task of constructing routes on a graph of the road network. It is even an order of magnitude simpler than the existing construction of routes, since it does not operate with probabilities, but has full information from the central dispatch. Even a home computer can cope with such a task, or rather many computers with a hierarchical structure of interconnections. Thus, AUTOMATIC central dispatching of all traffic in real time becomes possible. That is, the problem of lack of information is completely solved. This is a simple and long-solved problem of constructing routes on a graph of the road network. It is even an order of magnitude simpler than the existing construction of routes, since it does not operate with probabilities, but has full information from the central dispatch. Even a home computer can cope with such a task, or rather many computers with a hierarchical structure of interconnections. Thus, AUTOMATIC central dispatching of all traffic in real time becomes possible. That is, the problem of lack of information is completely solved. This is a simple and long-solved problem of constructing routes on a graph of the road network. It is even an order of magnitude simpler than the existing construction of routes, since it does not operate with probabilities, but has full information from the central dispatch. Even a home computer can cope with such a task, or rather many computers with a hierarchical structure of interconnections. Thus, AUTOMATIC central dispatching of all traffic in real time becomes possible. That is, the problem of lack of information is completely solved. AUTOMATIC central dispatching of all traffic in real time becomes possible. That is, the problem of lack of information is completely solved. AUTOMATIC central dispatching of all traffic in real time becomes possible. That is, the problem of lack of information is completely solved.
At the same time, central dispatching + full continuous video surveillance solves an extremely important problem of information reliability that is practically unsolvable by other means. How in systems CarToX guarantee that you get reliable information from other cars, and not fake from hackers?
5. There are many possible solutions, so conflicts are inevitable. And one plan
Have you ever wondered where conflicts and rudeness on the road come from? From multivariate! That is, when there are competing options that are strictly not registered in the SDA, there will always be conflicts.
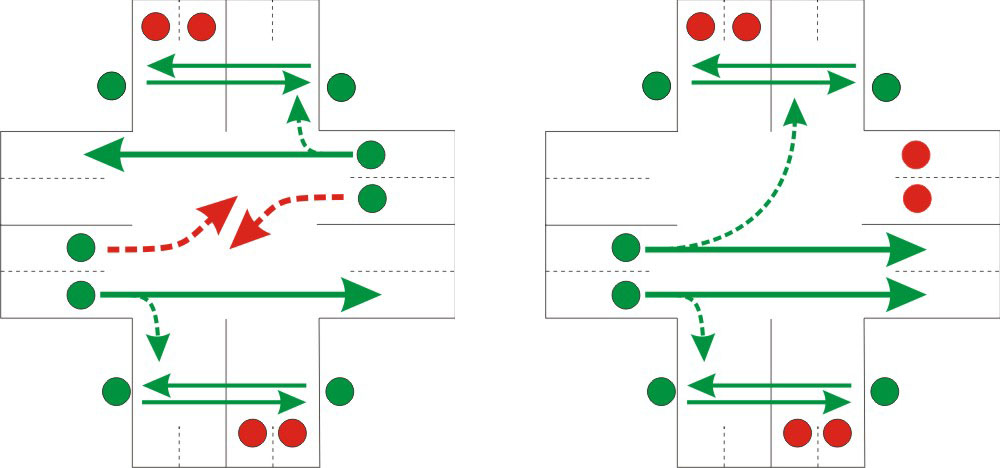
And nothing can be done with this, since for any person there are only two options: his opinion and the wrong opinion. But the way to resolve any conflict situations is well known - it is an independent arbitrator. Automatic central dispatching can act as such arbiter. Moreover, why do we need an arbitrator? We do not need an arbitrator! After all, an arbitrator is needed to resolve conflict situations that arise, but we have a planned movement, which the arbitrator himself plans. That is, it is sufficient at the planning stage to create a plan in such a way that potential conflict situations simply do not arise. Then neither conflicts, nor automobile rudeness on their basis will be in principle!
6. Who is to blame and what to do with it
Anyone who has faced with the analysis of the accident, knows that the true culprit is unequivocally very difficult to establish. Objective information is not available or it is not enough, and the witnesses are often the interested persons themselves. And the problem here is fundamental, since, in principle, the correct, in this context safe, trajectory is missing from the existing traffic rules. That is, if both drivers grossly violated the traffic rules, and both drove through a double solid to the oncoming lane, but left at the same time without a collision, then this incident will not even get into the reports. And if one driver strictly follows the traffic rules and brakes directly, then there will be a head-on collision. Moreover, in the court of this driver can even be found guilty, since he did not fulfill another paragraph of the traffic rules and did not do everything possible to avoid a collision. And the traffic rules are full of such contradictions. As a result almost always, at least in something, you can blame any driver. Please note that the traffic police, which created such contradictory traffic rules, will always have nothing to do with it. On the other hand, it is clear that it is impossible to paint all potentially dangerous cases. But there is a solution! It is necessary that automatic central dispatch prescribes the RIGHT trajectory of each transport. This can be done very simply with the most reliable and simple graphic modeling. That is, no two paths on the road plan should ever intersect. Thus, the first to deviate from its correct trajectory is to blame. As a result, the issue of responsibility is always solved objectively and unequivocally. will always have nothing to do with it. On the other hand, it is clear that it is impossible to paint all potentially dangerous cases. But there is a solution! It is necessary that automatic central dispatch prescribes the RIGHT trajectory of each transport. This can be done very simply with the most reliable and simple graphic modeling. That is, no two paths on the road plan should ever intersect. Thus, the first to deviate from its correct trajectory is to blame. As a result, the issue of responsibility is always solved objectively and unequivocally. will always have nothing to do with it. On the other hand, it is clear that it is impossible to paint all potentially dangerous cases. But there is a solution! It is necessary that automatic central dispatch prescribes the RIGHT trajectory of each transport. This can be done very simply with the most reliable and simple graphic modeling. That is, no two paths on the road plan should ever intersect. Thus, the first to deviate from its correct trajectory is to blame. As a result, the issue of responsibility is always solved objectively and unequivocally. This can be done very simply with the most reliable and simple graphic modeling. That is, no two paths on the road plan should ever intersect. Thus, the first to deviate from its correct trajectory is to blame. As a result, the issue of responsibility is always solved objectively and unequivocally. This can be done very simply with the most reliable and simple graphic modeling. That is, no two paths on the road plan should ever intersect. Thus, the first to deviate from its correct trajectory is to blame. As a result, the issue of responsibility is always solved objectively and unequivocally.
7. Interaction issues

So, all conflicts in the planned central dispatch system are excluded. It remains to add a device that interacts with each participant with the central dispatching system and, already through it, with all other road users. For this purpose, an individual traffic light (IC) for cars and pedestrians is installed in each vehicle, which provides permanent two-way communication with the automatic dispatcher. It consists of two screens, one inside the car for the driver and the other in front of the car for pedestrians. Thus, absolutely all intersections and junctions become traffic-controlled and all restrictions are contextual. At the same time physically, traffic lights and road signs are not needed anywhere at all. I.e,
8. Interaction with pedestrians

How to plan actions of pedestrians? And they do not need to plan, it is enough to safely manage them. Indeed, from a security point of view, while a pedestrian is on the sidewalk, he is not interested in the road safety system. That is, where and how pedestrians walk on the sidewalk does not affect safety in any way (collision of pedestrians with each other is not fatal).
Thus, it is enough for us to guarantee the safety of crossing the road by pedestrians in places convenient for a pedestrian. To do this, an “Individual traffic light” (IC) for pedestrians is installed in front of each car (red and green LED strip at the top of the windshield outside the car). Since this pedestrian IS is controlled by a common automatic central dispatch, it guarantees the safety of pedestrians. And since this traffic light moves with cars, a pedestrian crossing can be anywhere where a dispatcher will give cars a command to stop in order to let pedestrians pass. That is, in any place where it is convenient to cross a pedestrian, but not at any time.
That is, very inconvenient off-street pedestrians become meaningless!

Central dispatch fully regulates the movement of pedestrians on the road and transport (improved adaptive traffic lights).
There are three fundamental differences from existing pedestrian traffic lights:
- Green existing pedestrian traffic lights do not guarantee safety (that a pedestrian will not be knocked down by a third-row road from a pedestrian that the pedestrian does not see), and a green IP guarantees security, since the central dispatch sees everything and controls all transport. That is, the green pedestrian IP will light up only when ALL cars in this area stop.
- The IC allows the pedestrian to safely cross the road at any place convenient for him, and the existing pedestrian traffic light (crossing) forces the pedestrian to become an intruder, since the probability of getting hit by a car is significantly less than the cost of hundreds of meters to the nearest crosswalk.
- All pedestrian traffic lights are “adaptive”, that is, a situation when there is no one, but the red light is completely out of date.
It remains only to agree on how the pedestrian will let the central dispatch know that he is going to cross the road. For example, you can simply write to the traffic regulations that such a request is to stop a pedestrian under a lantern or a transition sign. At the same time, no “call” buttons for pedestrians are needed.
Thus, in such a system, if a pedestrian is certainly not a suicide, then he will never go to the red light of the IC, since it is GUARANTEED dangerous.
9. Lack of time to respond
Since we have a guaranteed safe plan and the exact coordinates of the entire transport, simply by subtracting two vectors (real from the planned one), at the earliest possible stage, we determine only potentially dangerous situations. This solves the problem of lack of time to respond. For example, now the driver sees that the oncoming car is slightly shifted to the center line. What to do? And nothing, since the reason for this shift is completely unknown: maybe the driver drives around the pit and then returns to his lane, or maybe the driver lost control and this is the initial phase of going into the oncoming lane?
Now, as they say, not everything is so simple!
The problem is that when the departure to the oncoming lane becomes obvious, the reaction time may not be enough. But the presence of a guaranteed safe trajectory in the plan completely solves this problem. In this example, it is precisely known that this is the initial phase of departure to the oncoming lane, since there is no pit detour in the plan. Consequently, this is the initial phase of loss of control and we must begin to respond.
10. And how to safely disperse
So there is a dangerous situation, conditionally, two cars are driving head-on. What to do? We need to make a coordinated decision (either both to the left or both to the right). So where, left or right? It is clear that the second will respond to the decision of the first. But who should turn first? Now there is no definite answer to these questions in principle (the unwritten rules are unwritten because they do not always work).

Bypassing the oncoming fool on the left
And here again the central dispatch system helps us out, which gives an unambiguous command, for example, both to the left (which contradicts both the written and unwritten rules) but does not lead to an accident.
11. What about cyclists?

Naturally, absolutely all road users who are constantly on the road, that is, everyone except for pedestrians, are required to connect and follow the instructions of the central dispatch. And cyclists, as the least protected transport, are most interested in this.
12. No fines needed.
Since the automatic dispatch is known for the plan and the reality, then already with a minimum deviation, even at the initial stage, a warning is issued. For example, if you press on the gas with the same intensity, then in a few seconds you will exceed the speed. If this minimum excess occurs by chance, the driver will correct and there will be no real speeding. Accordingly, there is simply nothing to fine him for! Similarly, with all other violations, for example, the driver simply will not receive permission to park in a prohibited place. Thus, the only violation that remains is the intentional (after several warnings) ignoring the dispatcher's commands. It is clear that the driver in respect of whom it is objectively and documented that he deliberately violated the traffic rules should not just be denied a driver’s license,
13. А что делать с неадекватными водителями и злостными нарушителями?
Why all these correct warnings, if they can be ignored, and accordingly it will be impossible to guarantee safety?

Two seconds, 22 corpses.
Therefore, in order to guarantee safety, that is, strict implementation of the plan, the “Individual Traffic Light” in each vehicle is connected to the vehicle’s control authorities and can remotely block any still potentially dangerous driver actions. This guarantees 100% road safety up to a technical failure. For this, the existing serial emergency braking systems need to be improved, using the possibilities of complete information and planned movement. That is, they will not work in some simplest situations, as they are now, but in absolutely all dangerous situations.
Thus, intentionally, the SDA can only be broken once. A ride without a license in the system of complete observation is impossible in principle.
14. Responsibility

Ever since kindergarten, parents teach children that: “Got on the road, you are responsible for your own safety.” And we must not look at the traffic lights, but at the cars, since not a single traffic light has killed any pedestrians yet. Otherwise you will be right, but dead. And got behind the wheel of a vehicle of increased danger, so you are responsible for everything.
And do drivers and pedestrians want to be responsible for the actions of other road users, which they cannot influence in any way? The question is not so stupid. Since, if there is logic in responsibility for one’s actions, then there is no logic in responsibility for others! Therefore, all responsibility for the organization of traffic should be assigned to the automatic central dispatch system, which has all the information and can directly influence the actions of all road users through the road and pedestrian Individual Traffic Lights. That is, Euclid is responsible for the safety of the plan with its geometry; specific programmers are responsible for the practical implementation of this geometry.
15. Why then the driver?
Since the driver essentially becomes only the performer, and the computer can be performed much better than a person, a full-fledged automatic car of the fifth level is obtained by itself, as a by-product. In this case, there is no point in a driver who safely drives a car, to prohibit the enjoyment of driving. Although the classic approach to an automatic car suggests in the long term a complete ban on "meat" drivers. But about this in the next article ...
The result: having consistently examined all the main problems of road traffic, we came to the conclusion that all of them can be completely solved. And the funny picture in the title of the article can in principle be implemented in practice.
This is the second article of the cycle. An overview of the principle of operation of such a system "ITS SPRUT" can be viewed in the first article of the link cycle
PS Since supporters of the
Immediately answer why I contacted the criticism of Vision Zero. The problem is that while Vision Zero is considered ideal and non-alternative, other concepts are simply not considered! What for? After all, we have the perfect solution Vision Zero, we have it in the road maps and that's it. Therefore, the leading Russian organization for innovation, the National Technological Initiative (STI), writes to me: “The project idea is recognized as expedient, but cannot be implemented within the Avtonet Roadmap, since it does not correspond to any of its directions, and cannot be CONSIDERATION Working Group Avtonet ".

To be continued …
