The classic confusion associated with the Big Bang
- Transfer
One of the most confusing properties of the Big Bang is associated with the expansion of the universe. Any reasonable person, having heard about the Big Bang, will imagine something expanding that he has already seen in life: a cloud of smoke exploding outward, or an exploding ball filled with air. It `s naturally. And, having imagined this, an intelligent person will ask the question: “But what is the universe expanding into?”
This reasonable, but, at first glance, paradoxical question is simply incorrectly asked. These are the consequences of what you imagined was completely wrong. I will try to correct your train of thought.
Let's go back and look at fig. 3 of the article about one-dimensional worlds. We reproduced the necessary part of this figure in fig. 1 in this article. Pay attention to two completely different representations of the aeolian line (measurements of possible wind directions, which include such directions as north, southeast, west-north-west, etc.). One of the representations is a straight line segment, the left end of which coincides with the right. Another is a loop on a plane. Just a second, you say, they look different. The loop surrounds a certain area, it has an inner and outer part. There is no such segment. So how can they portray the same thing?
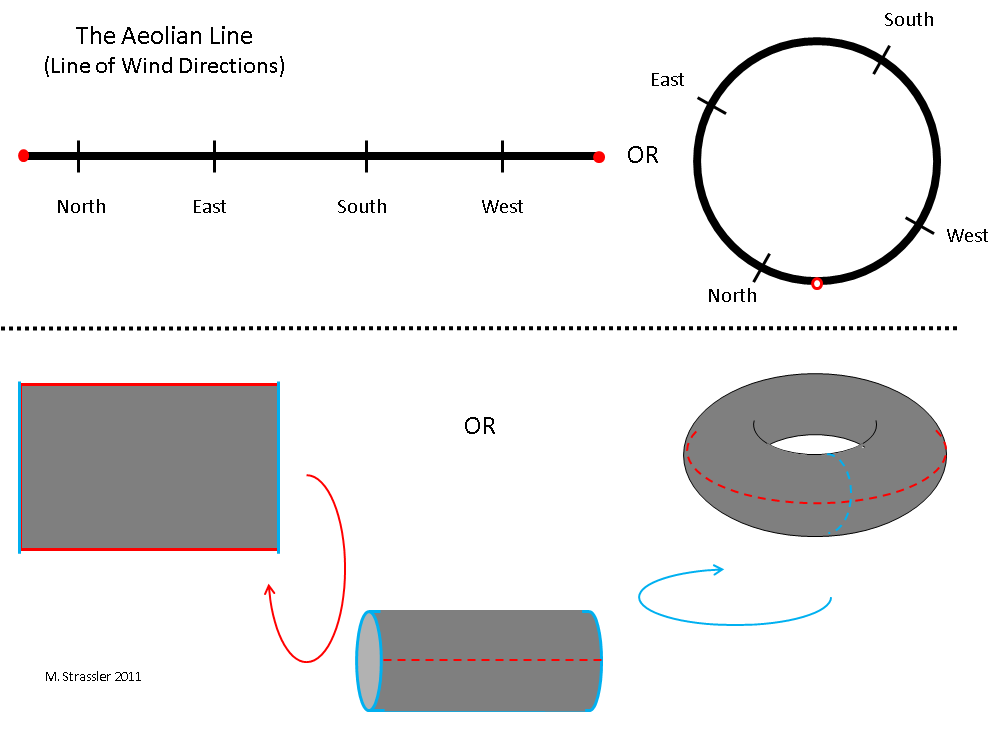
Fig. 1
Yes, this is, indeed, an extremely important question, and the answer to it is necessary for understanding spaces. Two images - a loop and a segment with two coincident ends - really represent the same one-dimensional eolian line. The area surrounded by the loop is only a property of the representation we have chosen, and not a property of the aeolian line itself! We must not confuse the properties of the images we use for visualization with the properties of spaces! This is easy to do, but it’s very important not to.
As another example, a donut (torus) is shown, which seems to have internal and external parts. But this is not so. Just as a circle can be represented by a segment with a left end coinciding with the right, so a torus can be represented as a rectangle in which the upper side coincides with the lower and the left with the right.
To check this, take a piece of paper. Connect the top edge to the bottom. You will get a cylinder. Use imagination to bend its right and left ends so that they touch - and you will immediately see that the torus should turn out.
A rectangle with matching sides does not have any “inside” and “outside”, so the cylinder or torus does not have this either. In other words, the properties of space can be studied if you travel inside it. To see that the circle has an inside and an outside, you need to cross it: but if your circle is an Aeolian line, then this is impossible. The wind cannot be asked to cross the circle from north to southeast. It can only move in a circle, across the east or across the west. Only the line itself is inherent in the Aeolian line!
Similarly, you cannot ask the tightrope walker with fig. 6 articles about one-dimensional worlds go from one part of a circular rope to another. The only safe option for his movement will be to circle. Therefore, the wind or tightrope walker cannot find out whether or not the circle has internal and external parts.
This concept is crucial to understanding the expansion of the universe. If you belong to the majority, you probably thought (as I did in my youth): “What is it expanding into?” In asking this question, you made the same mistake that applies to the circle: you confused something expanding with the idea of something expanding.
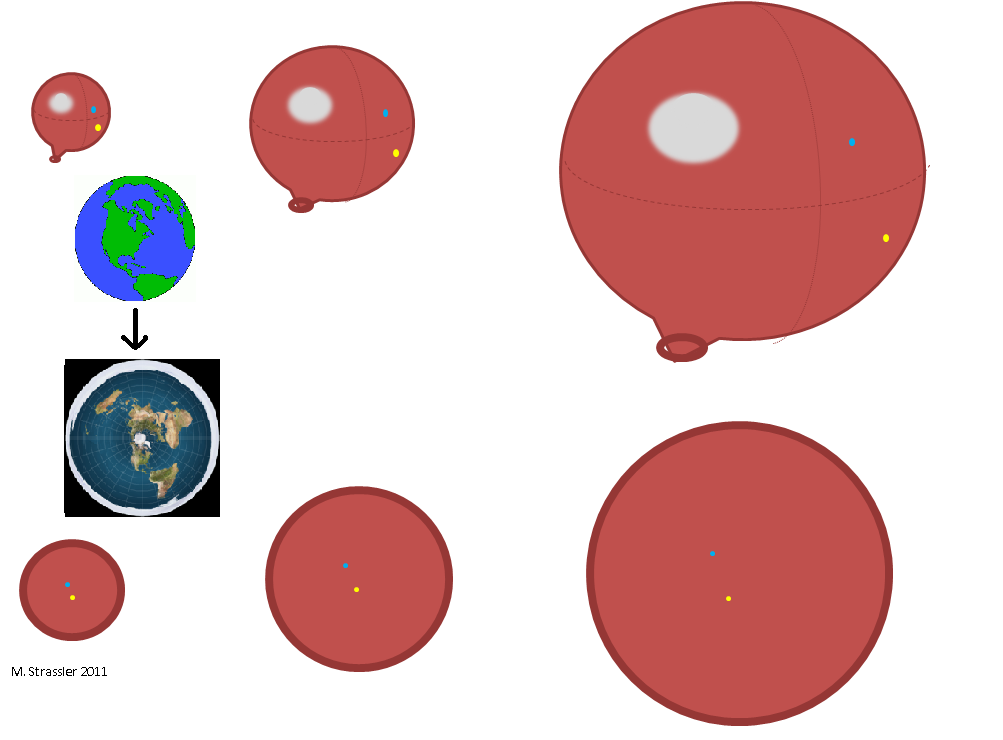
Fig. 2
For example, you can imagine an expanding ball. The ball looks to us as if it expands into a larger three-dimensional space in which it is located. But if you were an ant on a ball, you would not know anything about any inner or outer parts there; you would only know that the space through which you are able to move has become larger. You could even, as an ant cartographer, imagine this space as a disk, whose edges are brought together at one point (for example, at that point through which the balloon is inflated). You would not think about the “inside” and “outside”, you would only know that the distance between the yellow and blue points (and between any pair of points on the ball) is growing.
Another two-dimensional surface is the surface of the Earth itself. Suppose you woke up one morning and the Earth’s surface doubled. You would not know if the view of the Earth has changed for an observer from outer space, or if the diameter of the Earth has grown. You would only be aware that a trip to work or for groceries takes longer than before.
The fact that the inner or outer part of the ball is a property of representing the expanding space, and not the space itself, is more obvious in the example with an infinite plane. The infinite plane may well expand, although it does not expand to anything. It fills the same space after expansion, as before it, just the distances between objects in space (for example, between the points shown in the figure) grow. The plane essentially grows in size, but it is not inside a larger space, and therefore, obviously, cannot expand into this larger space. It just can expand, that's all.
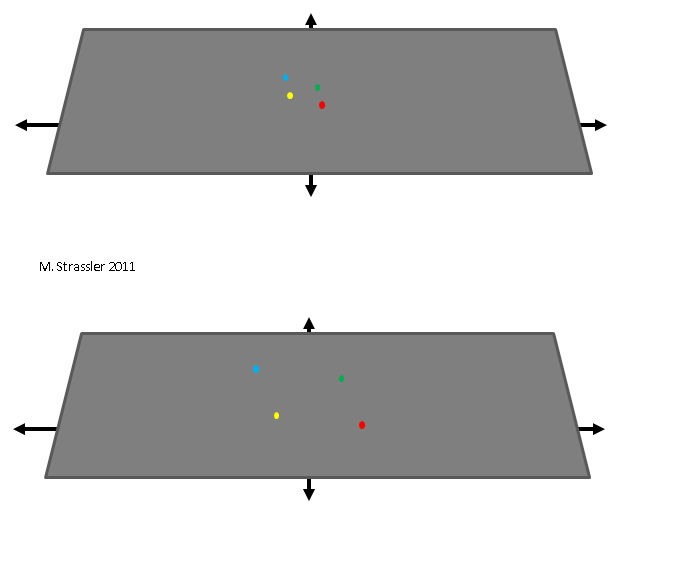
Fig. 3
So with the universe. As the plane just described, the space of the Universe is simply expanding. You cannot see it from the outside, there is simply no “outside”. But the expansion of the Universe can be determined even on the plane itself: the distance between any large objects of the Universe (in particular, between galaxies, huge universal star cities) grows and grows as the Universe expands. Over time, traveling from one galaxy to another will take more and more time. That is what the Big Bang did: took small sections of space and turned them into huge ones. It was not an explosion, it was not like a bomb explosion. This is an extension of the space itself.
This reasonable, but, at first glance, paradoxical question is simply incorrectly asked. These are the consequences of what you imagined was completely wrong. I will try to correct your train of thought.
Let's go back and look at fig. 3 of the article about one-dimensional worlds. We reproduced the necessary part of this figure in fig. 1 in this article. Pay attention to two completely different representations of the aeolian line (measurements of possible wind directions, which include such directions as north, southeast, west-north-west, etc.). One of the representations is a straight line segment, the left end of which coincides with the right. Another is a loop on a plane. Just a second, you say, they look different. The loop surrounds a certain area, it has an inner and outer part. There is no such segment. So how can they portray the same thing?

Fig. 1
Yes, this is, indeed, an extremely important question, and the answer to it is necessary for understanding spaces. Two images - a loop and a segment with two coincident ends - really represent the same one-dimensional eolian line. The area surrounded by the loop is only a property of the representation we have chosen, and not a property of the aeolian line itself! We must not confuse the properties of the images we use for visualization with the properties of spaces! This is easy to do, but it’s very important not to.
As another example, a donut (torus) is shown, which seems to have internal and external parts. But this is not so. Just as a circle can be represented by a segment with a left end coinciding with the right, so a torus can be represented as a rectangle in which the upper side coincides with the lower and the left with the right.
To check this, take a piece of paper. Connect the top edge to the bottom. You will get a cylinder. Use imagination to bend its right and left ends so that they touch - and you will immediately see that the torus should turn out.
A rectangle with matching sides does not have any “inside” and “outside”, so the cylinder or torus does not have this either. In other words, the properties of space can be studied if you travel inside it. To see that the circle has an inside and an outside, you need to cross it: but if your circle is an Aeolian line, then this is impossible. The wind cannot be asked to cross the circle from north to southeast. It can only move in a circle, across the east or across the west. Only the line itself is inherent in the Aeolian line!
Similarly, you cannot ask the tightrope walker with fig. 6 articles about one-dimensional worlds go from one part of a circular rope to another. The only safe option for his movement will be to circle. Therefore, the wind or tightrope walker cannot find out whether or not the circle has internal and external parts.
This concept is crucial to understanding the expansion of the universe. If you belong to the majority, you probably thought (as I did in my youth): “What is it expanding into?” In asking this question, you made the same mistake that applies to the circle: you confused something expanding with the idea of something expanding.

Fig. 2
For example, you can imagine an expanding ball. The ball looks to us as if it expands into a larger three-dimensional space in which it is located. But if you were an ant on a ball, you would not know anything about any inner or outer parts there; you would only know that the space through which you are able to move has become larger. You could even, as an ant cartographer, imagine this space as a disk, whose edges are brought together at one point (for example, at that point through which the balloon is inflated). You would not think about the “inside” and “outside”, you would only know that the distance between the yellow and blue points (and between any pair of points on the ball) is growing.
Another two-dimensional surface is the surface of the Earth itself. Suppose you woke up one morning and the Earth’s surface doubled. You would not know if the view of the Earth has changed for an observer from outer space, or if the diameter of the Earth has grown. You would only be aware that a trip to work or for groceries takes longer than before.
The fact that the inner or outer part of the ball is a property of representing the expanding space, and not the space itself, is more obvious in the example with an infinite plane. The infinite plane may well expand, although it does not expand to anything. It fills the same space after expansion, as before it, just the distances between objects in space (for example, between the points shown in the figure) grow. The plane essentially grows in size, but it is not inside a larger space, and therefore, obviously, cannot expand into this larger space. It just can expand, that's all.

Fig. 3
So with the universe. As the plane just described, the space of the Universe is simply expanding. You cannot see it from the outside, there is simply no “outside”. But the expansion of the Universe can be determined even on the plane itself: the distance between any large objects of the Universe (in particular, between galaxies, huge universal star cities) grows and grows as the Universe expands. Over time, traveling from one galaxy to another will take more and more time. That is what the Big Bang did: took small sections of space and turned them into huge ones. It was not an explosion, it was not like a bomb explosion. This is an extension of the space itself.
