TAU for the smallest: an example of the implementation of the PID controller in Unity3D
- Tutorial
Instead of introducing
Automatic control systems (ACS) are designed to automatically change one or more parameters of the control object in order to establish the required mode of operation. An automatic control system ensures the maintenance of the constancy of the set values of the controlled parameters or their change in accordance with a given law or optimizes certain criteria for the quality of control. For example, such systems include:
- stabilization systems
- software control systems
- tracking systems
This is a fairly wide class of systems that can be found anywhere. But what does this have to do with Unity3D, and probably games in particular? In principle, direct: self-propelled guns are implemented in any game that uses simulation as a gameplay element, such games include, for example, Kerbal Space Programm, Digital Combat Simulator (formerly Lock On), Strike Suit Zeroetc. (who knows more examples - write in the comments). In principle, any game that simulates real physical processes, including just kinematics with dynamics of motion, can implement these or those self-propelled guns - this approach is simpler, more natural, and the developer already has a set of ready-made tools provided by all sorts of Vyshnegradsky, Lyapunov, Kalman , Chebyshev and other Kolomogorovs, so you can do without the invention of a bicycle, because it has already been invented, so much so that a separate science has turned out: The theory of automatic control. The main thing here is not to overdo it. Only one problem here: they do not talk about TAU everywhere, not to everyone, often little and not very clear.
A bit of theory
The classic automatic control system shown in the following figure:
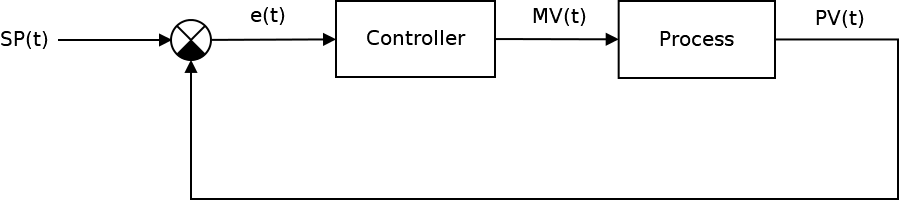
The key element of any self-propelled guns is the regulator, which is a device that monitors the state of the control object and provides the required control law. The management process includes: computing or control signal error error e ( t ) as the difference between the desired setting (set point or SP ) and the current process value (process vale or PV ), then the controller generates control signals (manipulated value, or MV ) .
One of the types of regulators is the proportional-integral-differentiating (PID) regulator , which generates a control signal, which is the sum of three terms: proportional, integral and differential.

Where, e ( t ) mismatch error, and also,P = K p ⋅ e ( t ) - proportional,I = K i ⋅ ∫ t 0 e ( τ ) d τ - integral,D = K d ⋅ d e ( t )d t - differential components (terms) of the control law, which in the final form is described by the following formulas
e ( t ) = S P ( t ) - P V ( t ) ,
M V ( t ) = K p ⋅ e ( t ) ⏟ P + K i ⋅ ∫ t 0 e ( τ ) d τ ⏟ I + K d ⋅ d e ( t )d t ⏟D,
The proportional component P - is responsible for the so-called proportional control, the meaning of which is that the output signal of the regulator counteracts the deviation of the controlled variable (mismatch errors or also called the residual) from the set value. The larger the mismatch error, the greater the command deviation of the controller. This is the simplest and most obvious control law. The disadvantage of the proportional control law is that the regulator never stabilizes at a given value, and an increase in the proportionality coefficient always leads to self-oscillations. That is why, in addition to the proportional control law, one has to use integral and differential.
The integral component I accumulates (integrates) the control error, which allows the PID controller to eliminate the static error (steady-state error, residual mismatch). Or in other words: the integral link always introduces a certain bias, and if the system is subject to some constant errors, then it compensates them (due to its bias). But if these errors are not present or they are neglectingly small, then the effect will be the opposite - the integral component will itself introduce a bias error. It is for this reason that it is not used, for example, in problems of ultra-precise positioning. A key disadvantage of the integral control law is the integrator windup effect.
The differential component D is proportional to the rate of change of the deviation of the controlled variable and is designed to counteract deviations from the target value that are predicted in the future . It is noteworthy that the differential component eliminates damped oscillations. Differential control is especially effective for processes that have large delays. The disadvantage of the differential control law is its instability to the effects of noise (Differentiation noise).
Thus, depending on the situation, P-, PD-, PI- and PID-controllers can be used, but the basic control law is mainly proportional (although in some specific tasks only differentiator and integrator links can be used).
It would seem that the issue of implementing PID controllers has long been beaten up and here on Habré there are a couple of good articles on this topic , including on Unity3D , there is also a good article PID Without a PhD ( translation ) and a series of articles in the journal "Modern Automation Technologies" in two parts: the first and second . Also at your service is an article on Wikipedia (for the most complete read the English version). And on the forums of the Unity3D community, no, no, and the PID controller will pop up like on gamedev.stackexchange
The question of the implementation of PID controllers is somewhat deeper than it seems. So much so that the young self-made, who decided to implement such a regulatory scheme, will find many wonderful discoveries, and the topic is relevant. So I hope this opus is useful to someone, so let's get started.
Attempt number one
As an example, let’s try to implement a control scheme using the example of turning control in a simple 2D space arcade, step by step, from the very beginning (didn’t forget that this is a tutorial?).
Why not 3D? Because the implementation does not change, except that you have to turn the PID control to control pitch, yaw and roll. Although the question of the correct application of PID control together with the quaternions is really interesting, I will sanctify it in the future, but even NASA prefers Euler angles instead of quaternions, so we'll get by with a simple model on a two-dimensional plane.
First, create the object itself, the game object of the spaceship, which will consist of the actual object of the ship at the top level of the hierarchy, attach to it a child object of Engine (purely for special effects). Here's what it looks like for me:
And we will throw on the object of the spacecraft in the inspector of all kinds of components. Looking ahead, I will give a screen of how it will look at the end:
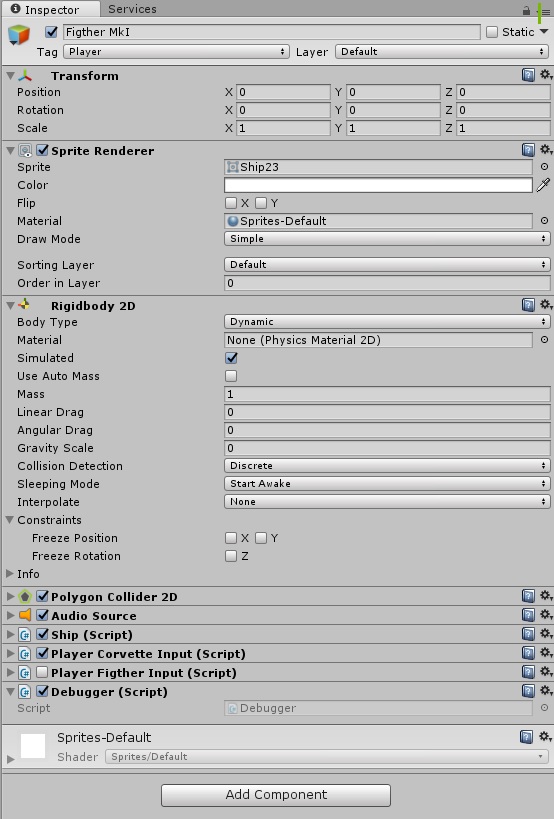
But this is later, but for now there are no scripts in it, only a standard gentleman's set: Sprite Render, RigidBody2D, Polygon Collider, Audio Source (why?).
Actually, physics is the most important thing for us now and control will be carried out exclusively through it, otherwise, the use of a PID controller would lose its meaning. We will also leave the mass of our spaceship at 1 kg, and all the coefficients of friction and gravity are equal to zero - in space.
Because in addition to the spaceship itself, there are a bunch of other, less intelligent space objects, then first we describe the parent class BaseBody , which will contain links to our components, methods of initialization and destruction, as well as a number of additional fields and methods, for example, for the implementation of celestial mechanics:
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespaceAssets.Scripts.SpaceShooter.Bodies
{
[RequireComponent(typeof(SpriteRenderer))]
[RequireComponent(typeof(AudioSource))]
[RequireComponent(typeof(Rigidbody2D))]
[RequireComponent(typeof(Collider2D))]
publicclassBaseBody : MonoBehaviour
{
readonlyfloat _deafultTimeDelay = 0.05f;
[HideInInspector]
publicstatic List<BaseBody> _bodies = new List<BaseBody>();
#region RigidBody
[HideInInspector]
public Rigidbody2D _rb2d;
[HideInInspector]
public Collider2D[] _c2d;
#endregion#region References
[HideInInspector]
public Transform _myTransform;
[HideInInspector]
public GameObject _myObject;
///<summary>/// Объект, который появляется при уничтожении///</summary>public GameObject _explodePrefab;
#endregion#region Audiopublic AudioSource _audioSource;
///<summary>/// Звуки, которые проигрываются при получении повреждения///</summary>public AudioClip[] _hitSounds;
///<summary>/// Звуки, которые проигрываются при появлении объекта///</summary>public AudioClip[] _awakeSounds;
///<summary>/// Звуки, которые воспроизводятся перед смертью///</summary>public AudioClip[] _deadSounds;
#endregion#region External Force Variables///<summary>/// Внешние силы воздйствующие на объект///</summary>
[HideInInspector]
public Vector2 _ExternalForces = new Vector2();
///<summary>/// Текущий вектор скорости///</summary>
[HideInInspector]
public Vector2 _V = new Vector2();
///<summary>/// Текущий вектор силы гравитации///</summary>
[HideInInspector]
public Vector2 _G = new Vector2();
#endregionpublicvirtualvoidAwake()
{
Init();
}
publicvirtualvoidStart()
{
}
publicvirtualvoidInit()
{
_myTransform = this.transform;
_myObject = gameObject;
_rb2d = GetComponent<Rigidbody2D>();
_c2d = GetComponentsInChildren<Collider2D>();
_audioSource = GetComponent<AudioSource>();
PlayRandomSound(_awakeSounds);
BaseBody bb = GetComponent<BaseBody>();
_bodies.Add(bb);
}
///<summary>/// Уничтожение персонажа///</summary>publicvirtualvoidDestroy()
{
_bodies.Remove(this);
for (int i = 0; i < _c2d.Length; i++)
{
_c2d[i].enabled = false;
}
float _t = PlayRandomSound(_deadSounds);
StartCoroutine(WaitAndDestroy(_t));
}
///<summary>/// Ждем некоторое время перед уничтожением///</summary>///<param name="waitTime">Время ожидания</param>///<returns></returns>public IEnumerator WaitAndDestroy(float waitTime)
{
yield return new WaitForSeconds(waitTime);
if (_explodePrefab)
{
Instantiate(_explodePrefab, transform.position, Quaternion.identity);
}
Destroy(gameObject, _deafultTimeDelay);
}
///<summary>/// Проигрывание случайного звука///</summary>///<param name="audioClip">Массив звуков</param>///<returns>Длительность проигрываемого звука</returns>publicfloatPlayRandomSound(AudioClip[] audioClip)
{
float _t = 0;
if (audioClip.Length > 0)
{
int _i = UnityEngine.Random.Range(0, audioClip.Length - 1);
AudioClip _audioClip = audioClip[_i];
_t = _audioClip.length;
_audioSource.PlayOneShot(_audioClip);
}
return _t;
}
///<summary>/// Получение урона///</summary>///<param name="damage">Уровень урона</param>publicvirtualvoidDamage(float damage)
{
PlayRandomSound(_hitSounds);
}
}
}It seems that they described everything that is necessary, even more than necessary (within the framework of this article). Now we will inherit from it the class of the Ship , which should be able to move and turn:
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespaceAssets.Scripts.SpaceShooter.Bodies
{
publicclassShip : BaseBody
{
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
publicfloat _rotation = 0f;
publicvoidFixedUpdate()
{
float torque = ControlRotate(_rotation);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
publicfloatControlRotate(Vector2 rotate)
{
float result = 0f;
return result;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 result = new Vector2();
return result;
}
}
}While there is nothing interesting in it, at the moment it is just a stub class.
We also describe the base (abstract) class for all BaseInputController input controllers:
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespaceAssets.Scripts.SpaceShooter.InputController
{
publicenum eSpriteRotation
{
Rigth = 0,
Up = -90,
Left = -180,
Down = -270
}
publicabstractclassBaseInputController : MonoBehaviour
{
public GameObject _agentObject;
public Ship _agentBody; // Ссылка на компонент логики корабляpublic eSpriteRotation _spriteOrientation = eSpriteRotation.Up; //Это связано с нестандартной // ориентации спрайта "вверх" вместо "вправо"publicabstractvoidControlRotate(float dt);
publicabstractvoidControlForce(float dt);
publicvirtualvoidStart()
{
_agentObject = gameObject;
_agentBody = gameObject.GetComponent<Ship>();
}
publicvirtualvoidFixedUpdate()
{
float dt = Time.fixedDeltaTime;
ControlRotate(dt);
ControlForce(dt);
}
publicvirtualvoidUpdate()
{
//TO DO
}
}
}Finally, the player controller class PlayerFigtherInput :
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespaceAssets.Scripts.SpaceShooter.InputController
{
publicclassPlayerFigtherInput : BaseInputController
{
publicoverridevoidControlRotate(float dt)
{
// Определяем позицию мыши относительно игрока
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем координаты указателя мышиfloat dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавишfloat targetAngle = Mathf.Atan2(dy, dx) * Mathf.Rad2Deg;
_agentBody._targetAngle = targetAngle + (float)_spriteOrientation;
}
publicoverridevoidControlForce(float dt)
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up
+ Input.GetAxis("Horizontal") * Vector2.right;
}
}
}It seems to be finished, now finally you can move on to what it was all about; PID controllers (didn’t forget hope?). Its implementation seems simple to disgrace:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceAssets.Scripts.Regulator
{
[System.Serializable] // Этот атрибут необходим для того что бы поля регулятора // отображались в инспекторе и сериализовывалисьpublicclassSimplePID
{
publicfloat Kp, Ki, Kd;
privatefloat lastError;
privatefloat P, I, D;
publicSimplePID()
{
Kp = 1f;
Ki = 0;
Kd = 0.2f;
}
publicSimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
publicfloatUpdate(float error, float dt)
{
P = error;
I += error * dt;
D = (error - lastError) / dt;
lastError = error;
float CO = P * Kp + I * Ki + D * Kd;
return CO;
}
}
}We take the default values of the coefficients from the ceiling: this will be the trivial unit coefficient of the proportional control law Kp = 1, a small value of the coefficient for the differential control law Kd = 0.2, which should eliminate the expected fluctuations and the zero value for Ki, which is chosen because in our software There are no static errors in the model (but you can always make them, and then fight heroically with the help of an integrator).
Now, let's return to our SpaceShip class and try to use our creation as a regulator for the rotation of a spaceship in the ControlRotate method:
publicfloatControlRotate(Vector2 rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибкуfloat angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}The PID controller will provide accurate angular positioning of the spacecraft only due to the torque . Everything is honest, physics and self-propelled guns, almost like in real life.
if (!_rb2d.freezeRotation)
rb2d.freezeRotation = true;
float deltaAngle = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
float T = dt * Mathf.Abs( _rotationSpeed / deltaAngle);
// Трансформируем угол в вектор
Quaternion rot = Quaternion.Lerp(
_myTransform.rotation,
Quaternion.Euler(new Vector3(0, 0, targetAngle)),
T);
// Изменяем поворот объекта
_myTransform.rotation = rot;using UnityEngine;
using Assets.Scripts.Regulator;
namespaceAssets.Scripts.SpaceShooter.Bodies
{
publicclassShip : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
publicfloat _targetAngle = 0f;
publicfloat _angle = 0f;
[Header("PID")]
public SimplePID _angleController = new SimplePID();
publicvoidFixedUpdate()
{
float torque = ControlRotate(_targetAngle);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
publicfloatControlRotate(float rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Вычисляем ошибкуfloat angleError = Mathf.DeltaAngle(_angle, rotate);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
//Кусок кода спецэффекта работающего двигателя радиif (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement;
return MV;
}
}
}
Everything? Going home?
WTF! What's happening? Why is the ship turning somehow weird? And why does he bounce so sharply from other objects? Is this stupid PID controller not working?
No panic! Let's try to figure out what is happening.
At the time of obtaining a new value of SP, there is a sharp (step) jump in the error mismatch, which, as we recall, is calculated like this: e ( t ) = S P ( t ) - P V ( t ) , respectively, a sharp jump in the derivative error occursd e ( t )d t that we compute in this line of code:
D = (error - lastError) / dt;You can, of course, try other differentiation schemes , for example, three-point, or five-point, or ... but still it will not help. Well, they don’t like derivatives of sharp jumps - at such points the function is not differentiable . However, it is worth experimenting with different schemes of differentiation and integration, but then not in this article.
I think that the time has come to build the graphs of the transition process : the stepwise effect from S (t) = 0 to SP (t) = 90 degrees for a body weighing 1 kg, a long arm of strength of 1 meter and a step of differentiation grid of 0.02 s - just like in our example on Unity3D (in fact, not quite, when building these graphs, it was not taken into account that the moment of inertia depends on the geometry of the solid, so the transition process will be slightly different, but still quite similar for demonstration). All values on the bar are given in absolute values: 
Hmm, what is happening here? Where did the response of the PID controller go?
Congratulations, we have just encountered such a thing as a kick. Obviously, at the time when the process is still PV = 0, and the set point is already SP = 90, then with numerical differentiation we get the value of the derivative of the order of 4500, which is multiplied by Kd = 0.2 and added to the proportional term, so that at the output we get the value angular acceleration is 990, and this is already a form of abuse of the physical Unity3D model (angular velocities will reach 18,000 deg / s ... I think this is the limiting value of the angular velocity for RigidBody2D).
- Maybe it’s worth picking up the coefficients with handles, so that the jump is not so strong?
- Not! The best thing that we can achieve in this way is a small amplitude of the jump in the derivative, however, the jump itself will remain so, and at the same time you can get to the complete inefficiency of the differential component.
However, you can experiment.
Attempt number two. Saturation
It is logical that the drive (in our case, the virtual SpaceShip shunting engines) cannot work out any arbitrarily large values that our crazy controller can give out. So the first thing we will do is to saturate the controller output:
publicfloatControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибкуfloat angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}namespaceAssets.Scripts.SpaceShooter.Bodies
{
publicclassShip : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
publicfloat _targetAngle = 0f;
publicfloat _angle = 0f;
publicfloat _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
publicvoidFixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
publicfloatControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибкуfloat angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * _thrust;
return MV;
}
publicvoidUpdate()
{
}
}
}The final scheme of our self-propelled guns will then become like this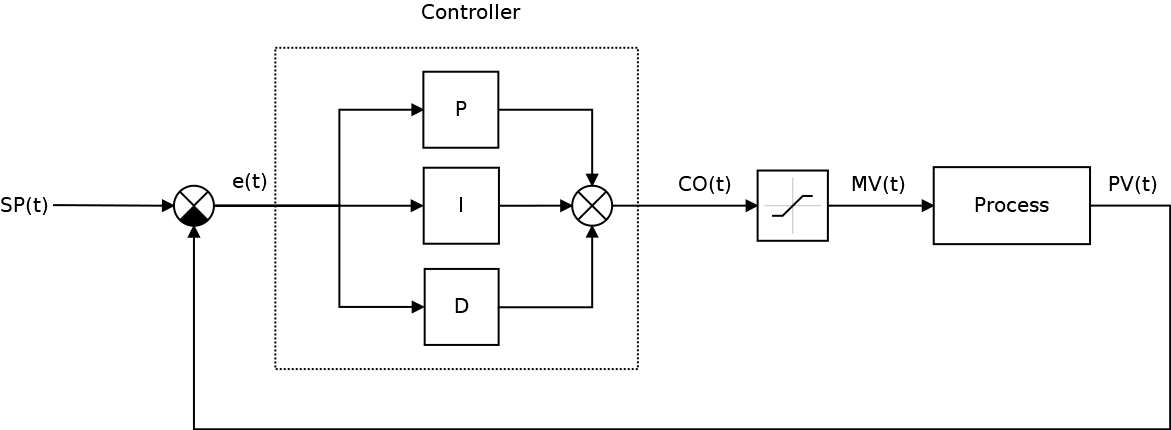
At the same time, it is already becoming clear that the output of the CO (t) controller is slightly different, as the controlled quantity of the process is MV (t) .
Actually, from this place you can already add a new game entity - a drive through which the process will be controlled, the logic of which can be more complicated than just Mathf.Clamp (), for example, you can introduce a discretization of values (so as not to overload the game physics with values coming in sixths after the decimal point), the dead zone (again, it does not make sense to overload the physics with ultra-small reactions), introduce a delay in the control and non-linearity (for example, a sigmoid) of the drive, and then see what happens.
Starting the game, we find that the spacecraft has finally become controllable:
If you build graphs, you can see that the controller’s reaction has become like this: 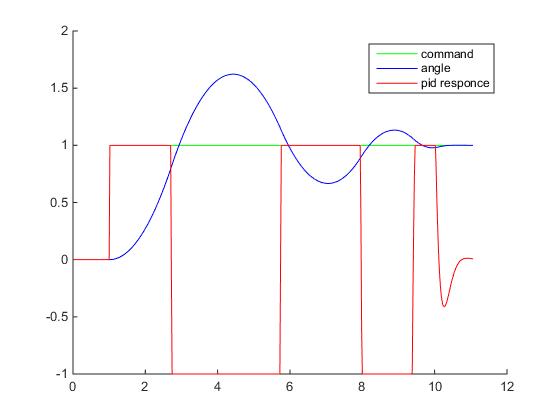
Normalized values are already used here, the angles are divided by the SP value, and the controller’s output is normalized to the maximum value at which saturation is already taking place.
Now the graph shows the presence of overshooting errors and damped oscillations. By decreasing Kp and increasing Kd, it is possible to reduce oscillations, but the controller reaction time (ship turning speed) will increase. And vice versa, by increasing Kp and decreasing Kd , it is possible to increase the reaction speed of the controller, but spurious oscillations will appear which, at certain (critical) values, will cease to be damped.
The following is a well-known table of the effect of increasing the PID controller parameters ( how to reduce the font, otherwise does the meringue transfer table not climb? ):
| Kp | Decrease | Increase | Slight changes | Decreases | Degrades |
| Ki | Decreases | Is increasing | Is increasing | Compensated if available | Degrades |
| Kd | Slight changes | Decreases | Decreases | Raises if Kd is small |
And the general algorithm for manual tuning of the PID controller is as follows:
- We select proportional coefficients for disconnected differential and integral links until self-oscillations begin.
- Gradually increasing the differential component we get rid of self-oscillations
- If a residual control error (bias) is observed, then we eliminate it due to the integral component.
There are no general values of the parameters of the PID controller: specific values depend solely on the parameters of the process (its transfer characteristic ): a PID controller that works perfectly with one control object will be inoperative with another. Moreover, the coefficients of the proportional, integral and differential components are also interdependent.
In general, we will not talk about sad things, the most interesting things will be waiting for us ...
Attempt number three. Derivatives Once Again
Having attached a crutch in the form of limiting the values of the controller output, we still did not solve the most important problem of our controller - the differential component does not feel well with a step change in the error at the controller input. In fact, there are many other crutches, for example, at the time of a spasmodic change in SP, "turn off" the differential component or put low-pass filters between SP (t) and the operationS P ( t ) - P V ( t ) due to which there will be a smooth increase in error, but you can completely turn around and show the real Kalman filter to smooth the input data. In general, there are many crutches, and ofcourse I would like toadd an observer , but not this time.
Therefore, we again return to the derivative of the mismatch error and carefully look at it:
d e ( t )d t =d(SP(t)-PV(t))d t =dSP(t)d t -dPV(t)d t ,
Didn’t notice anything? If you look closely, you can find that, in fact, SP (t) does not change in time (except for the moments of step change, when the controller receives a new command), i.e. its derivative is zero:
d S P ( t )d t =0,
then
d e ( t )d t =-dPV(t)d t ,
In other words, instead of the derivative error, which is not differentiable everywhere, we can use the derivative of the process, which in the world of classical mechanics is usually continuous and differentiable everywhere, and the scheme of our self-propelled guns will already take the following form:
e ( t ) = S P ( t ) - P V ( t ) ,
C O ( t ) = K p ⋅ e ( t ) ⏟ P + K i ⋅ ∫ t 0 e ( τ ) d τ ⏟ I - K d ⋅ d P V ( t )d t ⏟D,
Modify the controller code:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceAssets.Scripts.Regulator
{
[System.Serializable]
publicclassSimplePID
{
publicfloat Kp, Ki, Kd;
privatefloat P, I, D;
privatefloat lastPV = 0f;
publicSimplePID()
{
Kp = 1f;
Ki = 0f;
Kd = 0.2f;
}
publicSimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
publicfloatUpdate(float error, float PV, float dt)
{
P = error;
I += error * dt;
D = -(PV - lastPV) / dt;
lastPV = PV;
float CO = Kp * P + Ki * I + Kd * D;
return CO;
}
}
}And change the ControlRotate method a bit:
publicfloatControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибкуfloat angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, _myTransform.eulerAngles.z, dt);
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}And-and-and-and-and-if ... if you start the game, then it turns out that in fact nothing has changed since the last attempt, which was to be proved. However, if we remove the saturation, the regulator's reaction schedule will look like this: 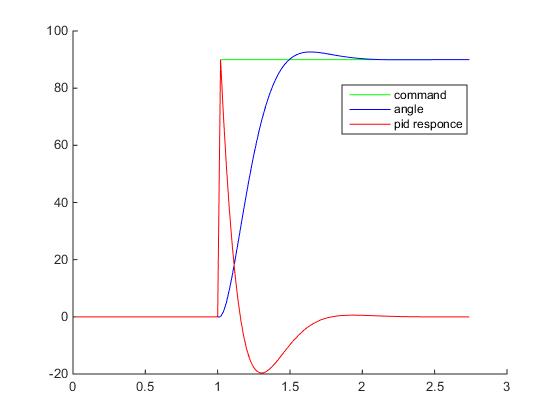
The CO (t) jump is still present, however, it is not as big as it was at the very beginning, and most importantly, it became predictable, because is provided exclusively by the proportional component, and is limited by the maximum possible mismatch error and the proportional coefficient of the PID controller (and this already hints that Kp makes sense to choose all the same less than unity, for example, 1 / 90f), but does not depend on the step of the differentiation grid ( i.e. dt) In general, I highly recommend using a derivative of the process rather than errors.
I think now no one will be surprised, but the same makar can be replaced K p ⋅ e ( t ) on- K p ⋅ P V ( t ) , but we will not dwell on this, you can experiment and tell in the comments what came out of it (most interesting)
Attempt number four. Alternative PID Implementations
In addition to the ideal representation of the PID controller described above, in practice the standard form is often used, without the coefficients Ki and Kd , instead of which time constants are used.
This approach is due to the fact that a number of tuning methods for the PID controller are based on the frequency characteristics of the PID controller and the process. Actually, the whole TAU revolves around the frequency characteristics of processes, so for those who want to delve deeper, and, suddenly, faced with an alternative nomenclature, I will give an example of the so-called PID controller standard form :
e ( t ) = S P ( t ) - P V ( t ) ,
C O ( t ) = C O b i a s + K p ⋅ ( e ( t ) + 1T i ⋅∫ t 0 e(τ)dτ-Td⋅dPV(t)d t ),
Where, T d = K dK p - differentiation constant, affecting the prediction of the state of the system by the regulator,
T i = K pK i is the integration constant affecting the error averaging interval by the integral link.
The basic principles for tuning a PID controller in standard form are similar to the idealized PID controller:
- an increase in the proportional coefficient increases speed and reduces the margin of stability;
- with a decrease in the integral component, the control error decreases faster with time;
- decrease in integration constant reduces stability margin;
- increase in differential component increases stability margin and speed
namespaceAssets.Scripts.Regulator
{
[System.Serializable]
publicclassStandartPID
{
publicfloat Kp, Ti, Td;
publicfloat error, CO;
publicfloat P, I, D;
privatefloat lastPV = 0f;
publicStandartPID()
{
Kp = 0.1f;
Ti = 10000f;
Td = 0.5f;
bias = 0f;
}
publicStandartPID(float Kp, float Ti, float Td)
{
this.Kp = Kp;
this.Ti = Ti;
this.Td = Td;
}
publicfloatUpdate(float error, float PV, float dt)
{
this.error = error;
P = error;
I += (1 / Ti) * error * dt;
D = -Td * (PV - lastPV) / dt;
CO = Kp * (P + I + D);
lastPV = PV;
return CO;
}
}
}The default values are Kp = 0.01, Ti = 10000, Td = 0.5 - at these values, the ship turns quickly enough and has a certain margin of stability.
In addition to this form of the PID controller, the so-called recursive form :
C O ( t k ) = C O ( t k - 1 ) + K p [ ( 1 + Δ tT i +TdΔ t )e(tk)+(-1-2TdΔ t )e(tk-1)+TdΔ t e(tk-2)]
We will not dwell on it, because It is relevant primarily for hardware programmers working with FPGAs and microcontrollers, where such an implementation is much more convenient and efficient. In our case - let's give something to piles on Unity3D - this is just one more implementation of the PID controller, which is no better than others and even less understandable, so once again we will rejoice together how to program well in cozy C #, and not in creepy and scary VHDL, for example.
Instead of a conclusion. Where else to add a PID controller
Now let's try to complicate the ship’s control a bit using dual-loop control: one PID controller, already familiar to us _angleController, is still responsible for angular positioning, but the second - a new one, _angularVelocityController - controls the speed of rotation:
publicfloatControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворотаfloat angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скоростиfloat angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}The purpose of the second regulator is to suppress excess angular velocities due to a change in torque - this is akin to the presence of angular friction, which we turned off when we created the game object. Such a control scheme [possibly] will make it possible to obtain a more stable behavior of the ship, and even get by with proportional control coefficients - the second regulator will absorb all vibrations, performing a function similar to the differential component of the first regulator.
In addition, we will add a new player input class - PlayerInputCorvette, in which the turns will be carried out by pressing the right-left keys, and we will leave target designation with the mouse for something more useful, for example, for controlling a turret. At the same time, we now have such a parameter as _turnRate - responsible for the speed / responsiveness of the turn (it is not clear just where to put it better in InputCOntroller or still Ship).
publicclassPlayerCorvetteInput : BaseInputController
{
publicfloat _turnSpeed = 90f;
publicoverridevoidControlRotate()
{
// Находим указатель мыши
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем относительные координаты указателя мышиfloat dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление указателя мыши
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
_agentBody._rotation -= Input.GetAxis("Horizontal") * _turnSpeed * Time.deltaTime;
}
publicoverridevoidControlForce()
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up;
}
}namespaceAssets.Scripts.SpaceShooter.UI
{
[RequireComponent(typeof(Ship))]
[RequireComponent(typeof(BaseInputController))]
publicclassDebugger : MonoBehaviour
{
Ship _ship;
BaseInputController _controller;
List<SimplePID> _pids = new List<SimplePID>();
List<string> _names = new List<string>();
Vector2 _orientation = new Vector2();
// Use this for initializationvoidStart()
{
_ship = GetComponent<Ship>();
_controller = GetComponent<BaseInputController>();
_pids.Add(_ship._angleController);
_names.Add("Angle controller");
_pids.Add(_ship._angularVelocityController);
_names.Add("Angular velocity controller");
}
// Update is called once per framevoidUpdate()
{
DrawDebug();
}
Vector3 GetDiretion(eSpriteRotation spriteRotation)
{
switch (_controller._spriteOrientation)
{
case eSpriteRotation.Rigth:
return transform.right;
case eSpriteRotation.Up:
return transform.up;
case eSpriteRotation.Left:
return -transform.right;
case eSpriteRotation.Down:
return -transform.up;
}
return Vector3.zero;
}
voidDrawDebug()
{
//Направление поворота
Vector3 vectorToTarget = transform.position
+ 5f * new Vector3(-Mathf.Sin(_ship._targetAngle * Mathf.Deg2Rad),
Mathf.Cos(_ship._targetAngle * Mathf.Deg2Rad), 0f);
// Текущее направление
Vector3 heading = transform.position + 4f * GetDiretion(_controller._spriteOrientation);
//Угловое ускорение
Vector3 torque = heading - transform.right * _ship._Torque;
Debug.DrawLine(transform.position, vectorToTarget, Color.white);
Debug.DrawLine(transform.position, heading, Color.green);
Debug.DrawLine(heading, torque, Color.red);
}
voidOnGUI()
{
float x0 = 10;
float y0 = 100;
float dx = 200;
float dy = 40;
float SliderKpMax = 1;
float SliderKpMin = 0;
float SliderKiMax = .5f;
float SliderKiMin = -.5f;
float SliderKdMax = .5f;
float SliderKdMin = 0;
int i = 0;
foreach (SimplePID pid in _pids)
{
y0 += 2 * dy;
GUI.Box(new Rect(25 + x0, 5 + y0, dx, dy), "");
pid.Kp = GUI.HorizontalSlider(new Rect(25 + x0, 5 + y0, 200, 10),
pid.Kp,
SliderKpMin,
SliderKpMax);
pid.Ki = GUI.HorizontalSlider(new Rect(25 + x0, 20 + y0, 200, 10),
pid.Ki,
SliderKiMin,
SliderKiMax);
pid.Kd = GUI.HorizontalSlider(new Rect(25 + x0, 35 + y0, 200, 10),
pid.Kd,
SliderKdMin,
SliderKdMax);
GUIStyle style1 = new GUIStyle();
style1.alignment = TextAnchor.MiddleRight;
style1.fontStyle = FontStyle.Bold;
style1.normal.textColor = Color.yellow;
style1.fontSize = 9;
GUI.Label(new Rect(0 + x0, 5 + y0, 20, 10), "Kp", style1);
GUI.Label(new Rect(0 + x0, 20 + y0, 20, 10), "Ki", style1);
GUI.Label(new Rect(0 + x0, 35 + y0, 20, 10), "Kd", style1);
GUIStyle style2 = new GUIStyle();
style2.alignment = TextAnchor.MiddleLeft;
style2.fontStyle = FontStyle.Bold;
style2.normal.textColor = Color.yellow;
style2.fontSize = 9;
GUI.TextField(new Rect(235 + x0, 5 + y0, 60, 10), pid.Kp.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 20 + y0, 60, 10), pid.Ki.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 35 + y0, 60, 10), pid.Kd.ToString(), style2);
GUI.Label(new Rect(0 + x0, -8 + y0, 200, 10), _names[i++], style2);
}
}
}
}namespaceAssets.Scripts.SpaceShooter.Bodies
{
publicclassShip : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
publicfloat _targetAngle = 0f;
publicfloat _angle = 0f;
publicfloat _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public SimplePID _angularVelocityController = new SimplePID(0f,0f,0f);
privatefloat _torque = 0f;
publicfloat _Torque
{
get
{
return _torque;
}
}
private Vector2 _force = new Vector2();
public Vector2 _Force
{
get
{
return _force;
}
}
publicvoidFixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement, _thrust);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
publicfloatControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворотаfloat angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скоростиfloat angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement, float thrust)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * thrust;
return MV;
}
publicvoidUpdate()
{
}
}
}And here is the final video of what should turn out:
Unfortunately, it turned out to cover not everything that we would like, in particular, the question of tuning the PID controller is almost not addressed, and the integral component is almost not consecrated - in fact, an example is given only for the PD controller. Actually, a few more examples were originally planned (cruise control, turret rotation and torque compensation), but the article has already swollen, and indeed:
Some links
- Good Wiki article
- PID tutorial
- PID controllers: implementation issues. Part 1
- PID controllers: implementation issues. Part 2
- PID Without a PhD
- PID Without a PhD. Transfer
- Derivative Action and PID Control
- Control System Lab: PID
- DIY PID controller
- Correct implementation of the difference scheme of the PID controller
- We program a quadrocopter on Arduino (part 1)
- Virtual quadrocopter on Unity + OpenCV (Part 1)
- Polyakov K.Yu. Theory of automatic control for dummies
- PID control system analysis, design, and technology
- Aidan O'Dwyer. Handbook of PI and PID Controller Tuning Rules (3rd ed.)
- PID process control, a “Cruise Control” example
- https://www.mathworks.com/discovery/pid-control.html
- http://scilab.ninja/study-modules/scilab-control-engineering-basics/module-4-pid-control/
- https://sourceforge.net/p/octave/control/ci/default/tree/inst/optiPID.m
Some more links to other examples
http://luminaryapps.com/blog/use-a-pid-loop-to-control-unity-game-objects/
http://www.habrador.com/tutorials/pid-controller/ 3-stabilize-quadcopter /
https://www.gamedev.net/articles/programming/math-and-physics/pid-control-of-physics-bodies-r3885/
https://ksp-kos.github.io/ KOS / tutorials / pidloops.html
Only registered users can participate in the survey. Please come in.
